
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительная частота события, аксиомы теории вероятностей. Классическое определение вероятностиСодержание книги
Поиск на нашем сайте
Заметим, что всякое событие есть некоторое высказывание о результатах рассматриваемого эксперимента. При многократном проведении опыта с соблюдением некоторого комплекса условий S возможны различные исходы: 1) в каждом из опытов можно наблюдать один и тот же результат; 2) ни в одном из опытов интересующий результат не появился; 3) в ряде опытов интересующий результат можно было наблюдать, а в оставшихся опытах этого не происходило. В первом случае говорят, что происходит достоверное событие. Во втором случае речь идет о невозможном событии. В третьем случае говорят, что происходит случайное событие. Однако случайность события по отношению к комплексу условий S не означает отсутствия всякой закономерной связи между ними. Будем обозначать случайные события большими латинскими буквами: A, B, C, D, F и т. д. Допустим, что производится серия из n одинаковых опытов. В каждом из опытов интересующее событие, назовем его А, может произойти или не произойти. В результате наблюдений за опытами замечено, что событие А появилось m раз, обозначим как m(А). Определение. Частотой события А (относительной частотой) называется величина, равная отношению числа опытов, в которых событие А произошло, ко всем проводимым опытам n, т.е. Экспериментально установлено, что для многих опытов, в которых рассматривается появление случайного события А, имеет место закон устойчивости относительных частот: если при неограниченном увеличении числа опытов n относительная частота события A Из определения видно, что частота имеет свойства: 1) m n (W)=1; 2) m n (Ø)=0; 3) 0 =< m n (A) <= 1; 4) m n (A+B)= m n (A)+m n (B), если события несовместны, т.е. такие, которые не могут происходить вместе. Из закона устойчивости относительных частот следует, что вероятность события является в некотором смысле пределом относительной частоты этого события. Поэтому свойства относительной частоты событий можно перенести в качестве аксиом на вероятность этих событий. 1) p (W) =1 - вероятность достоверного события равна 1; 2) p (Ø) = 0 - вероятность невозможного события равна 0;
3) 0 =< p (A) = < 1 - это означает, что вероятность любого события не может быть меньше 0 и больше 1. 4 ) аксиома конечной аддитивности: если события A и B несовместны, то p (A+B) = p (A) +p (B). На основании этих аксиом можно получить формулу для классического определения в ероятности: Р (А) = m / n, (1.1) т.е. вероятность любого события есть величина, равная отношению числа m опытов (исходов), в которых событие А произошло, к общему числу проводимых опытов n, причем возможность появления каждого из элементов одинакова. Пример 1.8. В ящике находятся 15 хороших деталей и 10 бракованных. Найти вероятность того, что при изъятии одной детали из ящика, она окажется бракованной (обозначим как событие А). Решение. Общее число деталей в ящике n = 15+10=25. Число исходов, соответствующих тому, что выбрана бракованная деталь, m = 10. Следовательно, вероятность того, что будет вынута бракованная деталь, равна Р(А) = m / n = 10/25= 2/3.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.173 (0.009 с.) |

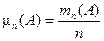 .
.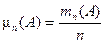 колеблется около некоторого числа p(A), то число p (A) называют вероятностью события A, а само это свойство называют законом устойчивости относительных частот.
колеблется около некоторого числа p(A), то число p (A) называют вероятностью события A, а само это свойство называют законом устойчивости относительных частот.


