
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные статистические распределения
Построение разного рода оценок и статистических критериев часто основывается на использовании ряда специальных распределений случайных величин. Нормальное распределение. Случайная величина
График плотности вероятности случайной величины, имеющей нормальное распределение, представлен на рисунке 3.5, на котором видно, что максимум функции находится в точке Поскольку нормальное распределение подробно изучается в курсе теории вероятностей, напомним свойства нормальной случайной величины, которые будут использоваться в дальнейшем.
Рис. 3.5 1) 2) Случайная величина называется центрированной, если ее математическое ожидание равно нулю. Для того чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:
3) Случайная величина называется нормированной, если ее дисперсия равна единице, а математическое ожидание равно нулю. Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратическое отклонение:
Центрированная и нормированная нормальная случайная величина называется стандартной. Таким образом, стандартной будет случайная величина
Вероятность попадания случайной величины
где Для стандартной нормальной случайной величины и симметричного промежутка формула (3.27) принимает следующий вид:
Распределение
имеет распределение хи-квадрат с
Рис. 3.6 С увеличением числа степеней свободы
Распределение Стьюдента. Пусть
имеет распределение Стьюдента с
На рис.3.7 приведены кривые стандартного нормального распределения (кривая 1) и плотности распределения Стьюдента (кривая 2).
Рис. 3.7 При На практике, как правило, используется не плотность вероятности, а квантиль распределения. Напомним, что квантилью порядка (или уровня) где
Рис. 3.8
Следующая теорема устанавливает свойства основных выборочных характеристик, вычисленных по выборке, соответствующих нормальному распределению. Теорема Фишера. Пусть 1) случайная величина 2) случайная величина 3) случайная величина Доказательство теоремы приведено в [2].
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.24.134 (0.007 с.) |
 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и 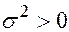 , что обозначается как
, что обозначается как  , если плотность вероятности этой случайной величины имеет вид
, если плотность вероятности этой случайной величины имеет вид . (3.25)
. (3.25)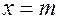 .
.
 ,
,  .
. .
. .
. ~
~  . (3.26)
. (3.26) , (3.27)
, (3.27)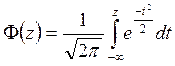 - интеграл вероятности, представляющий собой функцию распределения стандартной нормально распределенной случайной величины. Интеграл вероятности табулирован. Его значения приведены в таблице В Приложения.
- интеграл вероятности, представляющий собой функцию распределения стандартной нормально распределенной случайной величины. Интеграл вероятности табулирован. Его значения приведены в таблице В Приложения. . (3.28)
. (3.28) (хи-квадрат). Если
(хи-квадрат). Если  ,
,  независимые стандартные нормальные случайные величины, то говорят, что случайная величина
независимые стандартные нормальные случайные величины, то говорят, что случайная величина (3.29)
(3.29)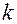 степенями свободы, что обозначается как
степенями свободы, что обозначается как  . Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.
. Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.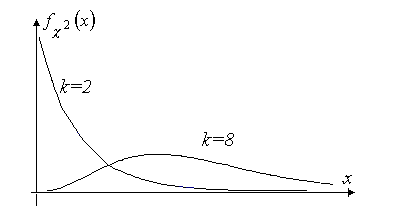
 плотность вероятности постоянно убывает, а при
плотность вероятности постоянно убывает, а при 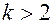 имеет единственный максимум
имеет единственный максимум  ,
,  ,
,  .
. ,
,  ,
, 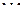 ,
,  - независимые стандартные нормальные случайные величины. Тогда случайная величина
- независимые стандартные нормальные случайные величины. Тогда случайная величина (3.30)
(3.30)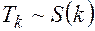 , при этом
, при этом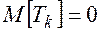 ,
,  .
.
 плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.
плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины. непрерывной случайной величины
непрерывной случайной величины  , которое удовлетворяет равенству
, которое удовлетворяет равенству 
 ,
, - функция распределения, а
- функция распределения, а 
 - случайная выборка из генеральной совокупности
- случайная выборка из генеральной совокупности 
 , тогда выборочное среднее
, тогда выборочное среднее  и несмещенная выборочная дисперсия
и несмещенная выборочная дисперсия  независимы, и при этом
независимы, и при этом имеет распределение
имеет распределение  ;
; имеет распределение
имеет распределение  ;
; имеет распределение
имеет распределение  .
.


