
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Углы между прямыми и плоскостямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теоретическая карта №3 Угол между прямой и плоскостью Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость [5, с. 43], [10, с. 51 ].
Угол φ между прямой АВ и её проекцией ВО на плоскость α (рис. 176) является наименьшим из всех углов, которые данная прямая образует с прямыми, проведенными на плоскости через точку В.
Угол между плоскостями Определение 1. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 178). Если φ тот из четырёх углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ, Очевидно, что 0°< φ≤90° [5, с.48].
Замечание. Напомним, что двугранный угол измеряется линейным углом, который образуется, если отметить на ребре двугранного угла какую – нибудь точку и в каждой грани из этой точки провести луч перпендикулярно к ребру (рис. 179).
Покажем иные способы построения линейного угла.
Определение 2. Пусть данные плоскости пересекаются (рис.182). Проведём плоскость, перпендикулярную их линии пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называют углом между данными плоскостями [10, с. 52].
Свойства некоторых углов Теорема о трёх косинусах. Пусть α – угол между наклонной l и её проекцией на плоскость τ, β – угол между проекцией наклонной l на плоскость τ и прямой р, проведённой через основание наклонной l в плоскости τ, γ – угол между наклонной l и прямой р (рис. 183). Тогда справедливо следующее равенство:
cos γ = cos α ∙cos β.
Теорема о биссектрисе угла. Для того, чтобы проекция прямой, проведённой через вершину угла, меньшего 180°, вне его плоскости являлась биссектрисой данного угла необходимо и достаточно, чтобы эта прямая составляла со сторонами угла равные острые углы.
Теорема о трёх синусах. В одной из граней двугранного угла, величина которого равна α, проведена прямая l, составляющая с ребром двугранного угла угол β (0<β<90°), а с другой его гранью угол γ (рис 185). Тогда справедливо следующее равенство:
sin γ = sin α ∙ sin β.
Теорема косинусов для трёхгранного угла Пусть α, β, γ – плоские углы трёхгранного угла, а φ – двугранный угол, противолежащий плоскому углу γ. Тогда справедливо следующее равенство
Доказательства утверждений теоретической карты №3 Теорема о трёх косинусах
АВ – наклонная к плоскости τ, ВО – её проекция; р – прямая: р Ì τ, ВÎ р; α – угол между наклонной АВ и её проекцией на плоскость τ, β – угол между проекцией
γ – угол между наклонной АВ и прямой р Доказать: cos γ = cos α ∙cos β. Доказательство. 1. Проведём ОК ^ р, АК. 2. Пусть АВ= х. 3. DАОВ - прямоугольный: ОВ= 4. DВОК - прямоугольный: ВК=ОВ×cos β, учитывая (3), ВК= 5. DАВК- прямоугольный: ВК= х ×cosγ.
Теорема о биссектрисе угла. Необходимость. Дано: ÐАВС (ÐАВС<180°), BD - прямая, проведённая через вершину угла вне его плоскости, ВО - её проекция на плоскость угла. ВО - биссектриса ÐАВС. Доказать: Ð1 = Ð2.
Доказательство
1.Проведём ОМ^ВС, ОР^АВ. Соединим точки D и M, D и P. 2. DОВМ=DОВР по гипотенузе и острому углу: ОВ – общая, ÐРВО=ÐМВО (ОВ – биссектриса). Следовательно, ВМ=ВР. 3. DDВМ и DDВР – прямоугольные (по теореме о трёх перпендикулярах) DDВМ=DDВР катету и гипотенузе: ВD – общая, ВМ=ВР (2). Следовательно, Второй способ. Воспользуемся теоремой о трёх косинусах. 1) Для наклонной DB, её проекции ОВ и прямой ВС:
2)Для наклонной DB, её проекции ОВ и прямой ВА:
Так как ОВ – биссектриса угла РВМ, то ÐОВМ=ÐОВР, следовательно, равны и косинусы этих углов, то есть cosÐ1=cosÐ2 и, следовательно, Ð1=Ð2. Достаточность (обратное утверждение) доказывается аналогично.
Теорема о трёх синусах
ÐАКО – линейный угол двугранного угла (АО^τ2, ОК^КВ, АК), ÐАКО= α; АВ – прямая: АВÌ τ1, ÐАВК=β, ÐАBО – угол, который составляет АВ с гранью τ2, ÐАВО=γ; Доказать: sin γ = sin α ∙ sin β Доказательство 1. Пусть АВ= х. 2. DАВК – прямоугольный, АК= 3. DАОК – прямоугольный, АО= 4. DАОВ – прямоугольный, АО= x sinγ 5. Из (3) и (4) x sinγ=
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 907; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |














 .
. Дано:
Дано: наклонной АВ и прямой р,
наклонной АВ и прямой р,

 6. Из (4) и (5): х ×cosγ =
6. Из (4) и (5): х ×cosγ =  , cosγ =
, cosγ =  .
. Первый способ.
Первый способ. .
. .
. .
.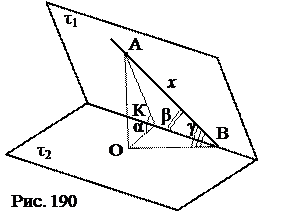 Дано: двугранный угол,
Дано: двугранный угол, .
. , учитывая (2) АО=
, учитывая (2) АО=  .
. .
.


