
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т.Е. Бондаренко, А.С. ПотаповСодержание книги
Поиск на нашем сайте
Т.Е. Бондаренко, А.С. Потапов ТЕОРЕТИЧЕСКИЕ КАРТЫ И ЗАДАЧИ ПО СТЕРЕОМЕТРИИ ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ В ПРОСТРАНСТВЕ
УГЛЫ МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ Учебно-методическое пособие по элементарной математике ВОРОНЕЖ
УДК 513 (07) ББК 22.151я7 Б81
Р е ц е н з е н т:
кандидат педагогических наук, почётный профессор Э.С. Беляева (ВГПУ)
Бондаренко Т.Е. Б81 Теоретические карты и задачи по стереометрии: параллельность и перпендикулярность в пространстве, углы между прямыми и плоскостями: учебно-методическое пособие по элементарной математике / Т.Е.Бондаренко, А.С. Потапов. - Воронеж: ВГПУ, 2011. – 126 с.
Пособие содержит теоретические сведения по следующим темам курса стереометрии: параллельность и перпендикулярность в пространстве, углы между прямыми и плоскостями, которые представлены в форме карт – справочников. К каждой карте подобран комплекс задач, при решении которых применяются приведённые в ней факты. Задачи сопровождаются чертежами, планами решений и ответами. Пособие предназначено для методического обеспечения курса элементарной математики в педагогическом вузе. Оно может быть использовано учителями средних общеобразовательных учреждений для подготовки учащихся к единому государственному экзамену по математике или для проведения элективного курса в условиях профильного обучения.
УДК 513 (07) ББК 22.151я7
© Бондаренко Т.Е., Потапов А.С.,2011 ПРЕДИСЛОВИЕ
Настоящее учебное пособие является продолжением книги «Теоретические карты и задачи по планиметрии». Оно предназначено для совершенствования подготовки студентов и школьников по стереометрии. Предполагается, что курс был предварительно изучен, но либо недостаточно качественно, либо забыт. Возникает необходимость восстановить ранее полученные знания и умения за достаточно сжатые сроки. Для этого полезно обладать целесообразными дидактическими материалами. Один из возможных вариантов таких материалов предлагается читателю. Выбор тематики пособия определялся востребованностью качественной подготовки абитуриентов и студентов по элементарной геометрии, в частности по стереометрии, и ее крайне низким уровнем. Пособие состоит из трёх основных разделов: «Параллельность в пространстве», «Перпендикулярность в пространстве», «Углы между прямыми и плоскостями». Перечисленные темы являются основополагающими для успешного формирования умения решать стереометрические задачи. Каждый раздел включает теоретическую карту по соответствующей теме, доказательства утверждений, содержащихся в ней, и комплекс задач, при решении которых используются утверждения из теоретической карты. В теоретической карте сосредоточены сведения, полезные при решении задач. Так как курс стереометрии предварительно изучен, то он может быть структурно переформирован. Каждая теоретическая карта объединяет тематически однородные сведения. Содержание таких сведений подобрано из школьных учебников по геометрии [1], [2], [5], [8], [10]. Однако ряд ценных для решения задач фактов остается за пределами учебников. Поэтому в теоретические карты вошли сведения из различных учебных пособий, перечисленных в списке литературы. Так, в раздел «Углы между прямыми и плоскостями» включены базисные задачи из книги И.Г. Габовича [4]. Доказательства утверждений, содержащихся в теоретических картах, приводятся с целью их изучения. Если такие доказательства имеются в школьных учебниках, то они не рассматриваются, а сопровождаются соответствующими ссылками на литературные источники. К каждой теоретической карте предлагаются комплексы задач. Они сопровождаются чертежами, планами решений и ответами. Читателю предлагается самостоятельно найти решение, однако, в случае затруднений, он может воспользоваться приведённым планом – алгоритмом. Мы по–прежнему считаем, что накопление опыта - один из способов научиться решать задачи самостоятельно. Задачи подобраны из различных книг, перечисленных в списке литературы. Настоящее учебное пособие может быть использовано преподавателями элементарной математики в педагогическом вузе, а также школьными учителями в процессе подготовки учащихся к единому государственному экзамену или в качестве содержательной основы элективного курса по стереометрии. Авторы выражают благодарность всем, принявшим участие в подготовке пособия к изданию. I. Параллельность в пространстве ТЕОРЕТИЧЕСКАЯ КАРТА № 1 Параллельность прямых Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются [5, с.9], [10, с.11].
Параллельность прямой и плоскости Определения 1. Прямая и плоскость называются параллельными, если они не имеют общих точек [5, с.11]. 2. Прямая и плоскость называются параллельными, если они не пересекаются, то есть не имеют общих точек [10, с.14].
Параллельность плоскостей Определение. Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек. [5, с.20], [ 10, с.15].
Параллельность прямых Доказательство признака параллельности прямых приводится в учебниках [5, с.11], [10, с.13]. Доказательство свойства параллельных прямых приводится в учебнике [5, с.10]. Параллельность плоскостей Доказательство признака параллельности плоскостей приводится в учебниках [5, с.20, 21], [10, с.15]. Параллельность прямых
№ 2 ( устно ). Дан параллелепипед. Доказать, что: а) для каждого его ребра в нём найдутся три ребра, ему параллельные (рис.13); б) для каждой диагонали его грани найдётся ей параллельная и равная диагональ в другой грани (рис. 14).
№ 3. Прямая в лежит в плоскости α и параллельна прямой а, не лежащей в этой плоскости. Через точку М плоскости α
План доказательства.
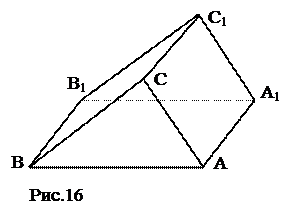
№ 4. Даны два параллелограмма АВВ1А1 и АСС1А1 (рис. 16). Доказать, что Δ АВС = Δ А1В1С1.
План решения. 1. ВВ1С1С – параллелограмм. 2. Δ АВС= Δ А1В1С1.
№ 5. Точка М находится вне плоскости параллелограмма ABCD. Найдутся ли параллельные средние линии у треугольников: а) МАВ и МАD;
План решения. а) 1. Р1- середина ребра DM, Р6- середина ребра DА, Р3- середина ребра MВ, Р5- середина ребра АВ. 2. Р1 Р6 || Р3 Р5.
№ 6. Точка М лежит вне плоскости треугольника АВС. Точки К, Р, Е, F – середины отрезков МА, АВ, МС, ВС. Как расположены прямые КР и ЕF?
1. Провести МВ. 2. КР||МВ, EF||MB. 3. КР|| EF. № 7. На рисунке 20 точки M, H, K, P – середины соответствующих отрезков AD и DC, BC и AB. Найти периметр четырёхугольника MHKP, если МР=8см, АС=32см.
План решения. 1. МНКР – параллелограмм. 2. РК. 3. РМНРК. Ответ: 48 см.
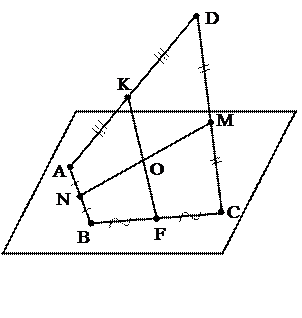
№ 8. Даны четыре точки, A, B, C, D, не лежащие в одной плоскости. Доказать, что прямые, соединяющие середины отрезков AB и CD, AD и BC пересекаются в одной точке.
План решения. 1. Провести АС. 2. Доказать, что NKMF – параллелограмм. 3. О – точка пересечения NM и KF.
№9. ABCDEF – замкнутая пространственная ломанная. Отрезки, соединяющие середины звеньев АВ и EF, ВС и ЕD, равны и параллельны. Параллельны ли звенья CD и AF?
№10. Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причём KP || MN, EF || AC. Доказать, что а) АС || KP; б) вычислить KP и MN, если КР:MN=3:5, АС=16 см.
а) EF || KP, EF ||AC. Вывод. б) 1. EF. 2. Выразить КР и MN через переменную. 3. Составить и решить уравнение
Ответ: 6 см, 10 см.
ТЕОРЕТИЧЕСКАЯ КАРТА №2 Перпендикулярность прямых Определения
2. Скрещивающиеся прямые называются перпендикулярными, если угол между ними равен 90° [10, c.50]. (Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым [10, c. 50]).
3. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°[5, c. 34].
Определения 1. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости [10, c.34].
2. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения [10,с. 26].
Определения 1. Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым [10, с. 32].
Перпендикулярность прямых Доказательство признака перпендикулярности прямых (1) приводится в учебнике Атанасяна [5,с. 34]. Доказательство признака перпендикулярности прямых (2) приводится в учебнике Погорелова [10, с.25] Перпендикулярность прямых № 1 (устно). Стороны четырёхугольника ABCD и прямоугольника A1B1C1D1 соответственно параллельны. Доказать, что ABCD – прямоугольник. № 2 (устно). Дан параллелепипед ABCD A1B1C1D1. Доказать, что 1) CD 2) AB^CC1 и DD1^A1B1, если AB^DD1.
№ 3 (устно). В тетраэдре DABC ВС^AD. Доказать, что AD^MN, где M и N – cередины рёбер AB и АC.
№ 4 (устно). РАВСD – правильная пирамида, Q – центр её основания. Как построить прямую, проходящую через точку Р и перпендикулярную прямой 1) AD; 2) AC; 3) PQ? 4)Как построить прямую, проходящую через точку К – середину ребра AD, перпендикулярно PQ? Рассмотреть решения для случая пересекающихся и скрещивающихся перпендикулярных прямых. Ответы обосновать. Ответы. 1) PK; прямая l: 2) PQ; прямая p: 3) прямая п: 4) KQ; прямая Теоретическая карта №3 Угол между плоскостями Определение 1. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 178). Если φ тот из четырёх углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ, Очевидно, что 0°< φ≤90° [5, с.48].
Замечание. Напомним, что двугранный угол измеряется линейным углом, который образуется, если отметить на ребре двугранного угла какую – нибудь точку и в каждой грани из этой точки провести луч перпендикулярно к ребру (рис. 179).
Покажем иные способы построения линейного угла.
Определение 2. Пусть данные плоскости пересекаются (рис.182). Проведём плоскость, перпендикулярную их линии пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называют углом между данными плоскостями [10, с. 52].
Свойства некоторых углов Теорема о трёх косинусах. Пусть α – угол между наклонной l и её проекцией на плоскость τ, β – угол между проекцией наклонной l на плоскость τ и прямой р, проведённой через основание наклонной l в плоскости τ, γ – угол между наклонной l и прямой р (рис. 183). Тогда справедливо следующее равенство:
cos γ = cos α ∙cos β.
Теорема о биссектрисе угла. Для того, чтобы проекция прямой, проведённой через вершину угла, меньшего 180°, вне его плоскости являлась биссектрисой данного угла необходимо и достаточно, чтобы эта прямая составляла со сторонами угла равные острые углы.
Теорема о трёх синусах. В одной из граней двугранного угла, величина которого равна α, проведена прямая l, составляющая с ребром двугранного угла угол β (0<β<90°), а с другой его гранью угол γ (рис 185). Тогда справедливо следующее равенство:
sin γ = sin α ∙ sin β.
Теорема о трёх косинусах
АВ – наклонная к плоскости τ, ВО – её проекция; р – прямая: р Ì τ, ВÎ р; α – угол между наклонной АВ и её проекцией на плоскость τ, β – угол между проекцией
γ – угол между наклонной АВ и прямой р Доказать: cos γ = cos α ∙cos β. Доказательство. 1. Проведём ОК ^ р, АК. 2. Пусть АВ= х. 3. DАОВ - прямоугольный: ОВ= 4. DВОК - прямоугольный: ВК=ОВ×cos β, учитывая (3), ВК= 5. DАВК- прямоугольный: ВК= х ×cosγ.
Теорема о биссектрисе угла. Необходимость. Дано: ÐАВС (ÐАВС<180°), BD - прямая, проведённая через вершину угла вне его плоскости, ВО - её проекция на плоскость угла. ВО - биссектриса ÐАВС. Доказать: Ð1 = Ð2.
Доказательство
1.Проведём ОМ^ВС, ОР^АВ. Соединим точки D и M, D и P. 2. DОВМ=DОВР по гипотенузе и острому углу: ОВ – общая, ÐРВО=ÐМВО (ОВ – биссектриса). Следовательно, ВМ=ВР. 3. DDВМ и DDВР – прямоугольные (по теореме о трёх перпендикулярах) DDВМ=DDВР катету и гипотенузе: ВD – общая, ВМ=ВР (2). Следовательно, Второй способ. Воспользуемся теоремой о трёх косинусах. 1) Для наклонной DB, её проекции ОВ и прямой ВС:
2)Для наклонной DB, её проекции ОВ и прямой ВА:
Так как ОВ – биссектриса угла РВМ, то ÐОВМ=ÐОВР, следовательно, равны и косинусы этих углов, то есть cosÐ1=cosÐ2 и, следовательно, Ð1=Ð2. Достаточность (обратное утверждение) доказывается аналогично.
Теорема о трёх синусах
ÐАКО – линейный угол двугранного угла (АО^τ2, ОК^КВ, АК), ÐАКО= α; АВ – прямая: АВÌ τ1, ÐАВК=β, ÐАBО – угол, который составляет АВ с гранью τ2, ÐАВО=γ; Доказать: sin γ = sin α ∙ sin β Доказательство 1. Пусть АВ= х. 2. DАВК – прямоугольный, АК= 3. DАОК – прямоугольный, АО= 4. DАОВ – прямоугольный, АО= x sinγ 5. Из (3) и (4) x sinγ= Угол между плоскостями №18. ABCDA1B1C1D1 – куб. Вычислить углы, образованные плоскостями:
План решения. 1. ÐВ1АВ - искомый угол. 2. tgφ, где ÐВ1АВ=φ. Ответ: 45°.
План решения. 1. ÐАОD - искомый угол.
Ответ: 90°.
3) АВ1D1 и АВС. План решения.
и АВС (l параллельна В1D1 или ВD). 2. ÐО1АО - искомый угол. 3. tgφ, гдеÐО1АО=φ. Ответ:
План решения. 1.О1 – центр верхнего основания. ÐAО1O - искомый угол. 2. tgφ, где ÐAО1O=φ. Ответ:
5) DА1C1 и BА1С1. План решения. 1. О1 – центр верхнего основания. ÐBО1D - искомый угол 2. BD, O1D, cosφ (DBO1D), где ÐBО1D =φ. Ответ:
Ответ:
План решения. 1. А1С1 ^ C1ВD (задача №22, с.20) 2. C1ВD ^ А А1С1. Ответ: 90°.
План решения. 1.Построения: АР ^ B1D, РС. 2. АР=РС, РС ^ B1D. 3. ÐАРС – искомый. 4. АР (из прямоугольного треугольника
5. АС. 6. cosφ, где ÐАРС =φ (по теореме косинусов). Ответ: φ=120°, угол между плоскостями 60°. №19. Дан правильный тетраэдр. Вычислить угол, образованный:
План решения. 1. Построения: О – центр основания; АК, РК; 2. ОК, РК выразить через ребро тетраэдра а; 3. cosφ, где ÐSKO=φ. Ответ: Все другие углы, образованные плоскостями граней тетраэдра равны найденному углу.
апофемы тетраэдра и плоскость основания; План решения. 1. Построения: SM, SK – апофемы, SMK – данная плоскость. P - середина MK, SP ^ MK, NP ^ MK, ÐSPN – искомый. 2. SP, NP, SN выразить через ребро тетраэдра а; 3. По теореме косинусов cosφ, где ÐSPN=φ.
3) плоскостью, проходящей через две апофемы тетраэдра и плоскостью боковой грани, не содержащей их; План решения. 1. Построения: SK, SР – апофемы, SРK – данная плоскость. l – линия пересечения плоскости SРK и
MS ^ l, NS ^ l, ÐMSN – искомый. 2. SN, NM, SM выразить через ребро тетраэдра а; 3. По теореме косинусов cosφ, где ÐMSN=φ. Ответ:
План решения. 1. Построения: MNPK, LNFK – сечения квадраты (рис. 228, 229). Они образованы средними линиями граней – треугольников. Рис. 230. О – середина NK. ОМ ^ NK, OF. ÐMOF – искомый. 2. Проверить равенство MF2 = OM2 + OF2. Сделать вывод. Ответ: 90°. №20 (устно). Две плоскости пересекаются. Какой угол образуют между собой плоскости биссекторов этих углов? Определение. Биссектором двугранного угла называется полуплоскость, которая делит данный угол на два равных по величине угла.
На рисунке α, β – данные плоскости, τ 1,τ2 – биссекторные плоскости.
№ 21 (устно). В треугольной пирамиде РАВС ребро РВ перпендикулярно плоскости грани АВС. Треугольник АВС равносторонний. Назвать угол между плоскостями: 1) РАВ и РВС (рис. 232); 2) РАС и ВАС (рис. 232); 3) РАС и РВС (рис. 233).
Ответ: 1) ÐАВС; 2) ÐРКВ; 3) ÐАLC. № 22 (устно). В основании четырёхугольной пирамиды РАВСD квадрат АВСD, ребро РВ перпендикулярно основанию. Назвать угол между плоскостями: 1) PAD и АВС; 2) PCD и АВС; 3) PAD и PCD.
Ответ: 1) Ð РАВ; 2) Ð РСВ. 3) Ð АКС.
4) PAD и PCВ.
Ответ: Ð АРВ.
№ 23. Основанием пирамиды служит квадрат. Две боковые грани пирамиды перпендикулярны к плоскости основания, а две другие образуют с ней двугранные углы, каждый из которых равен α. Высота пирамиды равна Н. Определить боковую поверхность пирамиды.
1. АВ ^ AD, PA ^ AD: ÐРАВ= α. 2. Аналогично ÐРСВ= α. 3. РB, AB, SDAPB. 4. SDAPB=SDCPB. 5. AP. 6. DAPD – прямоугольный. SDAPD.
8. Sбоковой поверхности пирамиды. Ответ: № 24. Основанием пирамиды служит прямоугольник, площадь которого равна S. Две боковые грани перпендикулярны к плоскости основания, а две другие наклонены к ней под углами 30° и 60°. Найти объём пирамиды.
1. Пусть АВ = а. Выразить РВ через а. 2. Пусть ВС = в. Выразить РВ через в. 3. Выразить РВ через S (перемножить результаты, полученные в (1) и (2)). 4. Найти объём пирамиды. Ответ: № 25. Основанием пирамиды служит ромб со стороной а. Две боковые грани пирамиды перпендикулярны к плоскости основания и образуют между собой тупой угол β, две другие боковые грани наклонены к плоскости основания под углом α. Найти боковую поверхность пирамиды.
1. Построения: ВК ^ AD, SK; BP ^ DC, SP. 2. ВК. 3. SВ. 4. SDSAB. 5. SК, SDSAD. 6. SDSAB= SDSСB, SDSAD= SDSСD.
Ответ: № 26. Основанием пирамиды служит прямоугольный треугольник, гипотенуза которого равна с. Боковая грань, проходящая через катет, прилежащий к острому углу α перпендикулярна к основанию, а две другие боковые грани наклонены к основанию под углом α. Определить объём пирамиды.
1. Построения: 1.1. PО ^ BC, PО ^ ABC. PО – высота пирамиды; 1.2. ОК ^ АВ, РК. 2. ÐРСО – угол между гранями АРС и АВС. ÐРКО – угол между гранями АРВ и АВС. ÐРСО =ÐРКО =α=ÐАВС. 3. АС, ВС, SDABС. 4. Точка О равноудалена от сторон АВ и АС, АО – биссектриса ÐА. 5. ОС. 6. ОР. 7.VPABC. Ответ: № 27. Основанием пирамиды служит прямоугольный треугольник, гипотенуза которого равна с, а острый угол α. Боковая грань, проходящая через гипотенузу перпендикулярна к основанию, а две другие боковые грани наклонены к основанию под углом α. Определить объём пирамиды.
1. Построения: 1.1. PО ^ АB, PО ^ ABC. PО – высота пирамиды; 1.2. ОК ^ АС, РК. 1.3. ОМ ^ ВС, РМ.
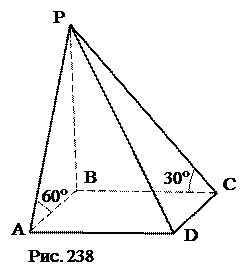
ÐРМО – угол между гранями CРВ и АВС. ÐРКО =ÐРМО =α=ÐABC. 3. АС, ВС, SDABС. 4. СО – биссектриса ÐС. 5. ОМ=МС= х. 6. DВОM~DВАС. 7. Найти х из пропорциональности сторон. 8. ОР. 9. VPABC. Ответ: № 28. Основанием пирамиды служит параллелограмм ABCD с площадью m 2, у которого диагональ BD перпендикулярна стороне AD. Двугранные углы при рёбрах AB и CD равны 60°, а при рёбрах AD и BC равны 45°. Найти боковую поверхность пирамиды.
Пусть РО – высота пирамиды. КМ – перпендикуляр к противоположным сторонам параллелограмма АВ и DС (ОÎКМ). Так как ÐРКМ=ÐРМК, то точка О равноудалена от сторон АВ и DC.
Аналогично BD – перпендикуляр к противоположным сторонам параллелограмма AD и BC (рис. 243) и из равенства углов PDB и PBD следует, что точка О равноудалена от сторон AD и BC. Свойством равноудалённости от противоположных сторон параллелограмма обладает точка пересечения его диагоналей (как центр симметрии). Таким образом, основание высоты пирамиды точка О – середина BD.
1. AD×BD = m 2. 2. BD= 3. AD×PD= 4. DAPD – прямоугольный. 5. S DAPD= 6. KM×DC= m 2. 7. KM=PM. 8. PM×DC= m 2. 9. S DPDC= 10. Sбоковой поверхности пирамиды. Ответ: № 29. Высота правильной четырёхугольной призмы равна Н. Через концы трёх рёбер, выходящих из одной вершины, проведена плоскость образующая с основанием угол α. Найти боковую поверхность призмы.
1. Построения: АВ1С, ÐВ1ОВ = α. 2. ОВ. 3. АВ. 4. Sбоковой поверхности призмы. Ответ: № 30. Через сторону основания, правильной четырёхугольной призмы проведено сечение, равновеликое боковой грани. Найти угол j, образованный сечением с плоскостью основания, если сторона основания призмы равна а, а высота h.
1. АМND – прямоугольник 2. ÐNDC – угол между плоскостью сечения и плоскостью основания, ÐNDC=j. 3. DD1=DN. 4. cosj. Ответ:
№ 31. Боковое ребро прямой треугольной призмы равно в, через сторону АС основания АВС проведено сечение АDС, площадь которого равна q. Найти объём призмы, если плоскость сечения образует с плоскостью основания угол α.
1. Построения: ADP, BP ^ AC, DP. DPB=Ðβ. 2. SDADC= 3. Выразить PD через РВ. 4. Подставить в формулу площади сечения и выразить площадь основания. 5.Vпризмы. Ответ: № 32. В правильной треугольной призме сторона основания равна 4 см, боковое ребро равно
1. Построения: 1.1. КРВ – сечение. 1.2. l – линия пересечения плоскости сечения и основания призмы, (l || КР). 1.3. О1 – середина КР. О1В ^ l, ВО ^ l (О- центр АВС). 1.4. Ð О1 ВО = 45°. 2. О1В1. 3. КВ1. 4. Поверхность меньшей части призмы ( 5. Поверхность призмы. 6. О1В. 7. S DKBP. 8. Поверхность большей части призмы. Ответ: № 33. Основанием наклонной призмы служит равнобедренный треугольник. Боковая грань призмы, проходящая через основание а равнобедренного треугольника, - квадрат и образует с двумя другими боковыми гранями углы, каждый из которых равен α. Найти боковую поверхность призмы.
1. Построения: РВ^ВВ1, РС^СС1. ÐCВР – угол между гранями ВВ1С1С и А А1В1В.
ВВ1С1С и А А1С1С. ÐCВР=ÐРCВ=α. 2. ВРС – перпендикулярное сечение. 3. РВ (DВРС). 4. Р(DВРС). 5.ВВ1. 6. Sбоковой поверхности призмы. Ответ: № 34. Боковое ребро наклонной призмы равно в, а площадь её основания равна S. Определить объём призмы, если известно, что плоскость, перпендикулярная к боковым рёбрам призмы, образует с плоскостью основания угол α.
1. Построения: 1.1. ВР ^ АА1, РС. Плоскость ВРС ^ АА1. 1.2. АК ^ ВС, РК, ÐАКР=α. Доказать.
2. Ð А1АО = ÐАКР=α. 3. А1О. 4. Vпризмы. Ответ: b Scosα. № 35. Правильная четырёхугольная призма пересечена плоскостью так, что в сечении получился ромб с острым углом α. Найти угол j плоскости сечения с плоскостью основания призмы.
1. Построения (рис. 251). 1.1 О – точка пересечения диагоналей призмы. 1.2. Прямая l: ОÎ l, l || АС, точки М, Р. 1.3. В1N = DD2. 1.4. MNPD2 – сечение. 2. Доказать MNPD2 – ромб (параллелограмм с перпендикулярными диагоналями). 3. ÐND2B2 =j. Доказать. (На чертеже n – линия пересечения плоскости сечения и плоскости А2В2С2D2, параллельной основанию призмы). 4. Пусть МР= а, тогда B2D2 = а. 5. Выразить ND2 через а. 6. cos j. Ответ: Свойства некоторых углов Теорема о трёх косинусах
План решения. 1.Построения. Прямая р: СÎ р, р || AB. 2. ZС – наклонная, АС –проекция, р – прямая в плоскости. В обозначениях теоремы о трёх косинусах ÐZCA=α, ÐACK=β, ÐZCK=γ γ – искомый угол. 3. Угол α. 4. Угол β. 5. cos γ (по теореме о трёх косинусах). 6. sinγ, tgγ. Ответ:
План решения. 1. Построения: ВО^τ, ÐВСО – искомый. 2. ÐВСА, ÐОСА. 3. ВС – наклонная, ОС – проекция, АС – прямая. cosÐВСО (по теореме о трёх косинусах). Ответ: 45°.
№ 38. Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами j1 |





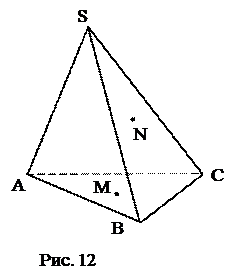 № 1 ( устно ). На боковых гранях призмы отмечены точки М и N. Как через эти две точки провести два параллельных отрезка? Решить аналогичную задачу, заменив призму пирамидой.
№ 1 ( устно ). На боковых гранях призмы отмечены точки М и N. Как через эти две точки провести два параллельных отрезка? Решить аналогичную задачу, заменив призму пирамидой.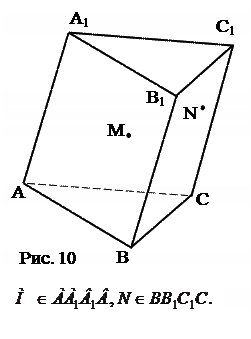



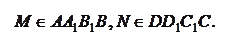
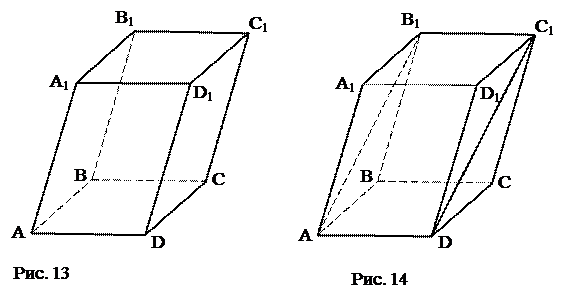
 проведена прямая с, параллельная прямой а. Доказать, что прямая с лежит в плоскости α.
проведена прямая с, параллельная прямой а. Доказать, что прямая с лежит в плоскости α.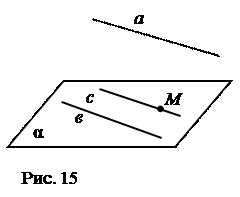
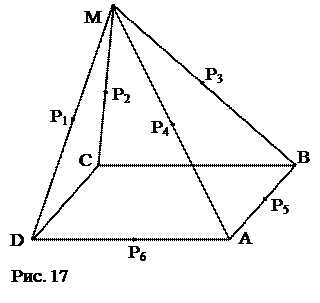 б) МАВ и МСD?
б) МАВ и МСD? б) Аналогично Р1Р2 || Р4Р3.
б) Аналогично Р1Р2 || Р4Р3. План решения.
План решения.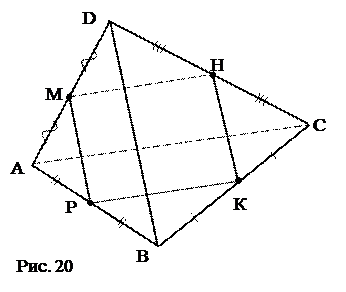

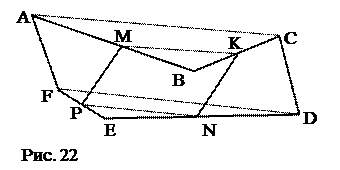 План решения. 1. MKNP – параллелограмм. 2. AC || FD. 3. AC = FD. 4. FACD – параллелограмм. 5. Вывод.
План решения. 1. MKNP – параллелограмм. 2. AC || FD. 3. AC = FD. 4. FACD – параллелограмм. 5. Вывод. План решения.
План решения.
 1. Две прямые называются перпендикулярными, если они пересекаются под прямым углом [10, c. 25].
1. Две прямые называются перпендикулярными, если они пересекаются под прямым углом [10, c. 25].







 2. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90° [5, с.52]. (Определение угла между плоскостями приведено на странице 73).
2. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90° [5, с.52]. (Определение угла между плоскостями приведено на странице 73). В1C1 и AB
В1C1 и AB 

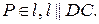













 Дано:
Дано: наклонной АВ и прямой р,
наклонной АВ и прямой р,

 6. Из (4) и (5): х ×cosγ =
6. Из (4) и (5): х ×cosγ =  , cosγ =
, cosγ =  .
. Первый способ.
Первый способ. .
. .
. .
.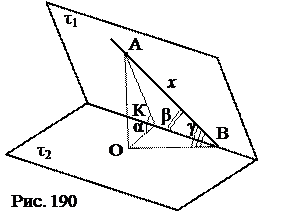 Дано: двугранный угол,
Дано: двугранный угол, .
. , учитывая (2) АО=
, учитывая (2) АО=  .
. .
. 1) АВ1С1 и АВС.
1) АВ1С1 и АВС.
 2) ВВ1D1 и АВС.
2) ВВ1D1 и АВС.

 1. l – линия пересечения плоскостей АВ1D1
1. l – линия пересечения плоскостей АВ1D1
 4) АВ1D1 и ВB1D1.
4) АВ1D1 и ВB1D1.


 Замечание. Можно воспользоваться DОО1D (рис. 222) и найти
Замечание. Можно воспользоваться DОО1D (рис. 222) и найти  .
.
 6) C1ВD и А А1С1.
6) C1ВD и А А1С1. 7) АВ1D и С В1D.
7) АВ1D и С В1D. AB1D, используя площадь).
AB1D, используя площадь). 1) плоскостями граней тетраэдра;
1) плоскостями граней тетраэдра; .
. 2) плоскостью, проходящей через две
2) плоскостью, проходящей через две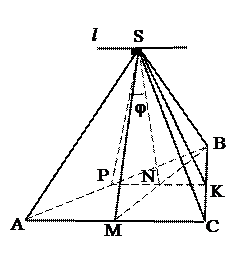 Ответ:
Ответ: 
 грани ASC, l || AC.
грани ASC, l || AC.


 4) плоскостями двух сечений, являющихся квадратами;
4) плоскостями двух сечений, являющихся квадратами;






 План решения.
План решения. 7. SDAPD= SDCPD.
7. SDAPD= SDCPD.
 План решения.
План решения.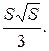
 План решения.
План решения. 7. Sбоковой поверхности пирамиды.
7. Sбоковой поверхности пирамиды.
 План решения.
План решения.
 План решения.
План решения. 2. ÐРКО – угол между гранями АРС и АВС.
2. ÐРКО – угол между гранями АРС и АВС.
 Рассмотрим фрагмент данной конфигурации (рис. 242).
Рассмотрим фрагмент данной конфигурации (рис. 242). План решения.
План решения. .
. .
. =SDBPC.
=SDBPC. m 2=SDAPB.
m 2=SDAPB.
 План решения.
План решения.
 План решения.
План решения.
 План решения.
План решения. . q =
. q = 
 . В призме проведено сечение через вершину основания параллельно противоположной стороне основания под углом 45°к плоскости основания. Найти поверхность большей части призмы.
. В призме проведено сечение через вершину основания параллельно противоположной стороне основания под углом 45°к плоскости основания. Найти поверхность большей части призмы. План решения.
План решения. .
.
 План решения.
План решения. Аналогично, ÐРCВ – угол между гранями
Аналогично, ÐРCВ – угол между гранями
 План решения.
План решения. 1.3. А1О ^АВС. А1О Ì А1АК. Доказать.
1.3. А1О ^АВС. А1О Ì А1АК. Доказать. План решения.
План решения.
 № 36. К плоскостиравностороннего треугольника АВС со стороной а через вершину А проведён перпендикуляр, на котором отложен отрезок AZ длиной а. Найти тангенс угла между прямыми AВ и ZC.
№ 36. К плоскостиравностороннего треугольника АВС со стороной а через вершину А проведён перпендикуляр, на котором отложен отрезок AZ длиной а. Найти тангенс угла между прямыми AВ и ZC.
 № 37. Проекция равностороннего треугольника на плоскость, проходящую через его сторону, является прямоугольным треугольником. Найти угол между стороной данного треугольника и плоскостью проекций.
№ 37. Проекция равностороннего треугольника на плоскость, проходящую через его сторону, является прямоугольным треугольником. Найти угол между стороной данного треугольника и плоскостью проекций.


