Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительный признак перпендикулярности прямыхСодержание книги
Поиск на нашем сайте
(теорема о трёх перпендикулярах) № 26 ( устно ). К плоскости прямоугольника ABCD проведен перпендикуляр СМ. Доказать, что прямая МD перпендикулярна прямой ВС.
1. MD ^ AD. 2. AD || BC. 3. Вывод. № 27. Катеты прямоугольного треугольника АВС равны 15 и 20. Из вершины прямого угла С проведён к плоскости этого треугольника перпендикуляр CD, равный 35. Найти расстояние от точки D до гипотенузы АВ.
1.CD ^ AB. 2. DM. План решения 1. АВ. 2. СМ. 3. DM. Ответ: 37. № 28. Стороны треугольника относятся как 10:17:21, а его площадь равна 84. Из вершины большего угла этого треугольника проведён перпендикуляр к его плоскости, равный 15. Найти расстояние от его концов до большей стороны.
Те же, что и задаче № 27. План решения. 1. Стороны DАВС (используя формулу Герона). 2. СК. 3. DK. Ответ: 8, 17. № 29 (устно). Из вершины А треугольника АВС проведён к его плоскости перпендикуляр AD. Из точки D опущен перпендикуляр на сторону ВС. При каких условиях этот перпендикуляр пройдёт через один из концов отрезка ВС?
Ответ: если ÐВ=90° или ÐС=90°. № 30. Вне плоскости параллелограмма ABCD взята точка К, отстоящая от сторон АВ и DC параллелограмма на расстояния, равные КМ и КЕ. Доказать, что МЕ – высота параллелограмма. Дополнительные построения. 1. КО ^ ABCD. 2. ОЕ ^ DC. 3. КЕ – заданное расстояние. 4. Аналогично КМ – заданное расстояние.
1. Доказать, что точки М, О, Е лежат на одной прямой. 2. Вывод. № 31. Через вершину В квадрата ABCD к его плоскости проведён перпендикуляр ВМ. Известно, что МВ = m, AB = n. Найти расстояние от точки М до сторон квадрата и до прямой АС.
1. МВ – расстояние от точки М до сторон АВ и ВС. 2. МВ = m. 3. МА – расстояние от точки М до стороны AD. 4. МА. 5. МС – расстояние от точки М до стороны DС. 6. МС. 7. МО – расстояние от точки М до стороны АС. 8. МО. Ответ: МВ = т, МА = МС = № 32 (устно). Существует ли четырёхугольная пирамида, у которой каждая боковая грань – прямоугольный треугольник?
Ответ: существует. Это пирамида в основании которой лежит прямоугольник, в частности, квадрат, и одно из боковых рёбер перпендикулярно к плоскости основания (рис. 156). № 33. Из вершины А прямоугольника ABCD проведён к его плоскости перпендикуляр АМ, конец М которого отстоит от других вершин на расстоянии 6, 7 и 9. Найти длину перпендикуляра АМ.
План решения. 1. DC. 2. AM. Ответ: 2. № 34. Основанием пирамиды служит квадрат, её высота проходит через одну из вершин основания. Определить боковую поверхность этой пирамиды, если сторона основания равна 20 см, а высота равна 21 см.
План решения. 1. Площадь DМВС и DАМВ. 2. МС. 3. Площадь DМСD и DМАD. 4. Площадь боковой поверхности данной пирамиды. Ответ: 1000. № 35. К плоскости квадрата ABCD проведён перпендикуляр ВР, равный 3 см. PD = 5см. Найти периметр треугольника АОС, где О – центр окружности, описанной около треугольника APD.
PD=5, BP=3, О – центр oкружности, описанной около DAPD. Найти: РDСОА. План решения. 1. BD=AC. 2. Центр О – середина PD. 3. ОР. 4. ОР=ОА. 5.ОА=ОС. 6.РDАОС . Ответ: 9. № 36. Основанием пирамиды служит равносторонний треугольник со стороной а. Одна из боковых граней также равносторонний треугольник и перпендикулярна к плоскости основания. Определить боковую поверхность этой пирамиды.
Построения. 1. SO^AC. 2. M – середина AB. 3. OK || CM.
План решения. 1. SDASC. 2. SO^ABC. 3. SK – высота DASB. 4. SO. 5. OK. 6. SK. 7. SDASB. 8. DASB=DCSB. 9. Sбоковой поверхности. Ответ: № 37. Основанием пирамиды служит правильный шестиугольник со стороной а. Одно из боковых рёбер перпендикулярно к плоскости основания и равно стороне основания. Определить боковую поверхность этой пирамиды.
План решения. 1. Построения: СЕ ^ FE, CA ^ AF (рис.162). 2. DSCD, DSEF –прямоугольные (рис. 161) 3. Площадь DSCD. 4. СЕ, SE, площадь DSEF. 5. Построения: СК^ ED, SK (рис. 163, 164).
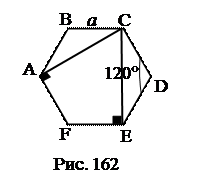
6. CK, SK, площадь DSED. 7. DSCD=DSCB, DSFE= DSAF, DSED=DSAF. 8.Боковая поверхность пирамиды. Ответ: № 38. Существует ли четырёхугольная призма, у которой сечение, проходящее через параллельные рёбра верхнего и нижнего основания – прямоугольник?
Ответ: существует. Это прямая призма, в основании которой лежит прямоугольник (квадрат). АВ1С1D – сечение – прямоугольник (рис. 165). Это наклонная призма, в основании которой лежит прямоугольник (квадрат) и две боковые грани перпендикулярны к плоскости основания (рис. 166). № 39. В правильной треугольной призме АВСА1В1С1 построить сечение, проходящее через точки А, М (А1М=МВ1), Р (ВР=РС). Найдите площадь сечения, если все рёбра призмы равны а.
1. АМ. 2. АР. 3. MK || AP. 4. KP. 5. AMKP – искомое сечение.
1. Дополнительные построения. Проведём КО^ВС. 2. АМКР – прямоугольная трапеция. (ÐР=ÐК=90°). 3. АР. 4. МК. 5. ОР. 6. КР. 7. SAMKP. Ответ: 4 0. Доказать, что диагональ куба и диагональ его грани, лежащие на скрещивающихся прямых, перпендикулярны.
1. А1С – наклонная, АС – её проекция на плоскость нижнего основания куба, 2. АС ^ BD. 3. Вывод. 4. Аналогично относительно диагоналей А1С и DC1. 41. Доказать, что диагональ куба А1С перпендикулярна плоскости ВС1D.
План доказательства. 1. А1С ^ BD. 2. А1С ^ DC1. 3. Вывод. № 42 (устно). Доказать, что диагональ основания правильной четырёхугольной пирамиды перпендикулярна её боковому ребру (рис. 171). № 43 (устно). Доказать, что сторона основания правильной треугольной пирамиды перпендикулярна её боковому ребру (рис. 172).
№ 44. В правильной треугольной пирамиде SABC сторона основания равна а и боковое ребро равно в. Провести в этой пирамиде плоскость через середины рёбер АВ и ВС параллельно ребру SB. Определить площадь полученного сечения.
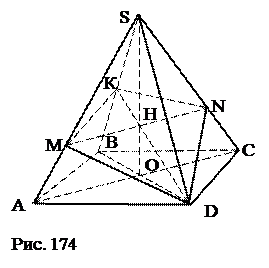
К, Р – середины АВ и ВС. 1. КР. 2. МК ||SB. 3. PN || SB. 4. KMNP – искомое сечение. Доказать. План решения. 1. KMNP – прямоугольник. 2. КР. 3. МК. 4. Площадь KMNP. Ответ: № 45. Пусть SABCD – правильная четырёхугольная пирамида, у которой боковое ребро равно диагонали основания. Через вершину основания пирамиды провести сечение, перпендикулярное противолежащему боковому ребру.
1. Точка К: ВК = KS. 2. DK. 3. Точка Н – пересечения DK и SO. 4. MN: HÎ MN, MN || AC. 5. DMKN – искомое сечение. Доказать.
№ 46. Основанием призмы является правильный треугольник, сторона которого равна а. Каждое боковое ребро призмы равно в, угол между одним из боковых рёбер и прилежащими к нему сторонами основания равен 45°. Найти боковую поверхность призмы.
1. А1О^АВС, точка ОÎАР, где АР – биссектриса ÐА. 2. АА1^ВС. 3. ВВ1С1С - прямоугольник. 4. 5.
Ответ:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.37.85 (0.009 с.) |

 План доказательства.
План доказательства. Дополнительные построения.
Дополнительные построения.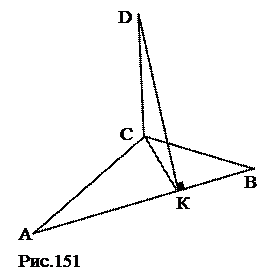 Дополнительные построения.
Дополнительные построения.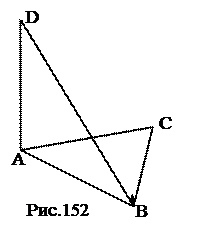

 План доказательства
План доказательства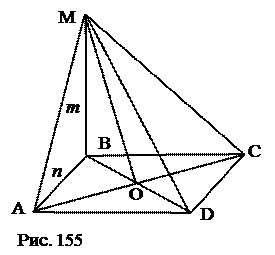 План решения.
План решения.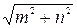 , МО =
, МО =  .
.
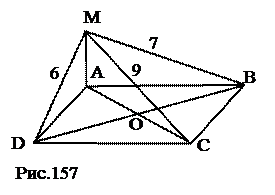

 Дано: ABCD – квадрат, ВP^ABCD,
Дано: ABCD – квадрат, ВP^ABCD,
 .
.


 .
.
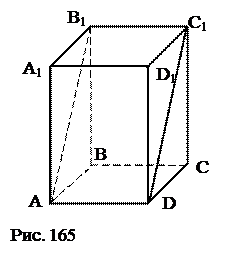
 План построения.
План построения. План решения.
План решения.
 План доказательства.
План доказательства.


 План построения сечения.
План построения сечения.
 План построения.
План построения. План решения.
План решения. .
. .
. 6. Sбоковой поверхности призмы.
6. Sбоковой поверхности призмы.