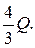Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дополнительные признаки параллельности прямыхСодержание книги
Поиск на нашем сайте
№ 37 (устно). SABCD – правильная пирамида. Как построить линию пересечения плоскостей граней SAD и SBC, SAB и SDC? Ответ обосновать.
№ 38 (устно). Изобразить параллелограмм ABCD и точку Р, не лежащую в плоскости этого параллелограмма. Отметить точки E, K, M, H – середины сторон AB, BC, CD и AD соответственно. Как построить линию пересечения плоскостей PEH и PKM? Ответ обосновать.
№ 39 (устно). АВСDA1B1C1D1 - куб. Как построить линию пересечения плоскости DA1C1 и плоскости грани АВС? Ответ обосновать.
№ 40. Основание пирамиды SABCD – трапеция ABCD. Построить сечение пирамиды плоскостью, проходящей через ребро AD и точку М, принадлежащую грани BSC.
1. KN || BC, МÎKN. 2. AK. 3. ND. 4. AKND – сечение. 5. Доказать, что сечение искомое.
№ 41. Треугольники ABC и DBC не лежат в одной плоскости и имеют общую сторону, точки М, Н и К – середины соответственно сторон BD, CD, AC. 1) Построить l линию пересечения плоскостей МКН и АВС. 2) Построить точку Р пересечения плоскости МКН и прямой АВ. 3) Найти РК, если ВС=8. 4) Доказать, что отрезки РН и МК пересекаются и в точке пересечения делятся пополам.
1) План построения. 3) 1. Прямая l: l Ì ABC, KÎ l, l || BC. 1. PK– средняя линия DBAC. 2. Доказать, что l – искомая линия 2. PK=4. пересечения плоскостей. 4) 2) План построения. 1.KH – параллелограмм, 1. P= l Ç AB. MK, PH – диагонали. 2. Доказать, что Р – искомая точка 2.Вывод. пересечения прямой и плоскости. № 42. Треугольник APD и трапеция ABCD имеют общую сторону AD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка PD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если AD = 10.
1. l – линия пересечения плоскостей BCK и PAD. l Ì ADP, KÎ l, l || AD. 2. M – точка пересечения прямой АР и плоскости ВСК. 3. МК – средняя линия DAPD, MK=5. № 43 ( устно ). Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны. Доказать по рисунку 74.
№ 44. В правильной треугольной пирамиде SABC сторона основания а и боковое ребро в. Провести в этой пирамиде плоскость через середины рёбер АВ и ВС параллельно ребру SB. Определить периметр полученного сечения.
1. MN. 2. MPÌSAB, MP || SB. 3. NQÌBSC, NQ || SB. 4. PQ. 5. MNQР – сечение. 6. Обосновать построение сечения. План вычисления.
Ответ: № 45. Построить сечение правильной четырёхугольной пирамиды, проходящее через середины двух смежных сторон основания и середину высоты. Вычислить периметр полученного сечения, если каждое ребро пирамиды равно а.
Пусть точки K, F – середины смежных сторон АВ и ВС основания пирамиды, Р - середина высоты. 1. KF. 2. В плоскости ASC через точку Р построить MN || AC (рис. 76). 3. Q = KF Ç BD. 4. QP. 5. L = QP Ç SD (рис. 77). 6. Обосновать, что KMLNF– искомое сечение (рис. 78).
План вычисления. 1. KF. 2. MK. 3. LQ. 4. LP. 5. Вид D MLN. 6. Вид D LPN. 7. PN. 8. LN. 9. PKMLNF. Ответ: №46 (устно). Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через вершины А, С и точку М ребра A1B1.
1. MP || A1C1. 2. АМРС – искомое сечение. 3.Обосновать, что АМРС– искомое сечение (рис. 79).
№ 47 ( устно). Через вершину тетраэдра проведена плоскость, параллельная противолежащей грани. Как построить линии пересечения этой плоскости с плоскостями остальных граней тетраэдра?
Назвать линии пересечения плоскости α с гранями BPA, APC, BPC и обосновать выбор.
№ 48. В кубе ABCDA1B1C1D1 середины К и L противолежащих рёбер АА1 и СС1 соединены отрезками прямых с вершинами куба В и D1. Определить вид получившегося четырёхугольника KBLD1 и найти его стороны и диагонали. Ребро куба равно а.
Ответ: ромб; № 49. В правильной четырехугольной призме ABCDA1B1C1D1 AB=1, AA1=4. Построить сечение призмы, параллельное АС и проходящее через точки D1 и К – середину AA1. Вычислить площадь полученного сечения.
1. КК1 || АС. 2. D1K. 3. D1K1. 4. l: l || D1K1, K Î l, KB. 5. p: p || D1K, K1Î p, K1B. 6. Обосновать, что D1KBК1 – искомое сечение. План вычисления. 1. Вид сечения. 2. КК1. 3. D1В.4. S
Ответ: 3. № 50. Основанием правильной призмы служит шестиугольник со стороной 3 дм; высота призмы равна 13 дм. Определить площадь сечения, проведённого через две противолежащие стороны верхнего и нижнего оснований призмы.
План построения. 1. Х – точка пересечения прямой FE и плоскости грани СС1DD1. 2. C1Х, точка N. 3. MF || C1N. 4. EN. 5. MB1 || EN. 6. Обосновать, что FMB1C1NE – искомое сечение. План вычисления. 1. 2. MN. 3. NE. 4. PN. 5. PE. 6. SFMNE. 7. № 51. На параллельных плоскостях α и β выбрано по паре точек А1, А2 и В1, В2 соответственно так, что прямые А1В1 и А2В2 пересекаются в точке S. Вычислить SA1 и SB2, если А1В1=6 см, SA2=2,5 см SB2 : SA2=3.
1. D SB1B2 ~ D SA1A2. 2. Коэффициент подобия. 3. SB2. 4. Выразить SA1через SB1. 5. SA1. Ответ: 1,5 см; 7,5 см.
Рассмотреть иное расположение заданных геометрических фигур (рис. 86) и решить задачу для второго случая.
№ 52. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А1, В1 и С1, а другую – в точках А2, В2 и С2. Докажите, что треугольники А1В1С1 и А2В2С2 подобны.
Доказать пропорциональность сторон треугольников А1В1С1 и А2В2С2 или равенство их углов. Рассмотреть иное расположение заданных геометрических фигур и решить задачу для второго случая.
№ 53. В правильной треугольной пирамиде SABC через SD и СЕ, где D – середина АВ, Е – середина SA проведены сечения пирамиды, параллельные между собой. Определить площадь большего из них, если площадь меньшего равна Q.
План построения. 1. ME || SD. 2. MC. 3. DР || MC. 4. SР. 5. SDР || EMC.
План вычисления. 1. ÐSDР = ÐEMС = j. 2. Выразить площадь D SDР через SD, DР и j. 3. Выразить SD через ME. 4. Выразить DР через MC. 5. Выразить площадь D SDР через ME, MC и j. 6. Выразить площадь D SDР через площадь D MEC. Ответ:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.76.183 (0.009 с.) |






 План построения.
План построения.

 1. 2. 3.4.
1. 2. 3.4.
 План решения.
План решения.
 План построения.
План построения. 1. MN. 2. MP. 3. PMNQP.
1. MN. 2. MP. 3. PMNQP.


 План построения.
План построения.




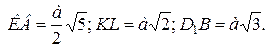
 План построения.
План построения. .
.

 =2SFMNE.
=2SFMNE. План решения.
План решения.
 Ответ: 3 см и 7,5 см.
Ответ: 3 см и 7,5 см. Указание.
Указание.