
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Промежуток времени между событиямиСодержание книги
Поиск на нашем сайте Еще одно важное следствие преобразований Лоренца – относительность промежутка времени. Напр. между началом и концом какого-либо процесса, происходящего в данной точке, т.е. зависимость этого промежутка времени от выбора инерц. СО. Пусть 2 события происх. в одной и той же т.А ( //Относит. неподвижн. СО К точка А движется с пост. ск-тью V, как и СО K'. Поэтому в СО К события 1 и 2 совершаются в различных точках пр-ва с координатами Преобраз. Лоренца имеют вид:
Из полученной формулы следует, что собственное время, т.е. время, измеряемое по часам, движущимся с данным объектом, меньше времени, отсчитанного по часам, движущимся относительно тела, т.А. Закономерность, рассмотренная нами, свидетельствует о существовании релятивистского эффекта замедления времени в движущейся ИСО по сравнению с неподвижной, значит все физ. процессы в этой подвижной СО замедляются.
Основной закон релятивистской динамики В релятивистской мех-ке, в отличие от классич, масса м.т. не постоянна, а зависит от ск-ти Ск-ть изменения импульса частицы равна силе
Это выр. явл. законом релятивистской мех-ки. Если на частицу действуют несколько сил, то под силой
Релятивистский закон взаимодействия массы и энергии Приращение кинетич. эн.
При ск-тях v<<c Из соотношения Тогда для полной кинетич. эн. можем записать Т.к. при ск-тях близких к ск-ти света потенц. эн. стремится к 0, то эн. релятивистской частицы определяется ее кинетич. эн. и полная эн. частицы = произведению релятивистской массы этого тела на квадрат ск-ти света в вакууме. Полная энергия частицы и импульс связаны соотношеним
Ур-ние Бернулли
Рассмотрим жидкость, движущуюся по трубе переменного сечения. Жидкость вытекает слева в сечении 1 с площадью Жидкость через течет через трубу под действием разности приложенных извне давлений За бесконечно малый промежуток времени Величину Сократив обе части ур-ния (1) на Это ур-ние наз. ур-нием неразрывности. Если умножить это ур-ние на При перемещении массы Полная работа Эта работа затрачена: 1)на увеличение кинетич. энергии элемента жидкости массой 2)на изменение потенц. энергии этого элемента объема в поле сил тяжести при переходе жидкости из уровня
Разделим обе части равенства 2 на объем Сгруппируем ур-ние 3 по индексам Поскольку сечение 1 и 2 выбраны произвольно, то сумма Ур-ние (5) наз. ур-нием Бернулли и выражает собой закон сохр. энергии при установившемся движении несжимаемой идеальной жидкости. Величина При движении элементарного объема жидкости происходит непрерывный переход энергии из одной формы в другую, но полная энергия этого объема остается неизменной.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.006 с.) |

 в момент времени
в момент времени  так, что промежуток времени между этими событиями
так, что промежуток времени между этими событиями  .
. .
. , т.к.
, т.к.  .
. 
 этой точки. Значение массы различно в двух движущихся друг относительно друга системах отсчета.
этой точки. Значение массы различно в двух движущихся друг относительно друга системах отсчета.  , где
, где  - масса покоя частицы, т.е. ее масса, измеренная в той СО, относит. кот. частица нах-ся в покое. Тогда из ур-ния для импульса
- масса покоя частицы, т.е. ее масса, измеренная в той СО, относит. кот. частица нах-ся в покое. Тогда из ур-ния для импульса  и учитывая релятивистскую массу мы можем записать для релятивистского импульса формулу.
и учитывая релятивистскую массу мы можем записать для релятивистского импульса формулу.  , где
, где  действующей на эту частицу.
действующей на эту частицу. .
. понимают равнодействующую силу.
понимают равнодействующую силу. частицы равно работе, совершаемой действующей на эту частицу силы
частицы равно работе, совершаемой действующей на эту частицу силы  , где
, где  - приращение релятивистской массы, т.к.
- приращение релятивистской массы, т.к.  .
. 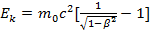 .
. мы имеем выр. кин. эн. для классич. мех-ки.
мы имеем выр. кин. эн. для классич. мех-ки. имеем: изменение энергии
имеем: изменение энергии 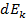 связано с изменением массы
связано с изменением массы  . Это соотношение справедливо и для других видов энергии.
. Это соотношение справедливо и для других видов энергии. . Это выр. устанавливает связь между энергией частицы и ее массой и явл. законом взаимосвязи массы и энергии.
. Это выр. устанавливает связь между энергией частицы и ее массой и явл. законом взаимосвязи массы и энергии.
 В 1738г. Бернулли вывел важное соотношение для установившего движения идеальной несжимаемой жидкости.
В 1738г. Бернулли вывел важное соотношение для установившего движения идеальной несжимаемой жидкости. , находящейся на высоте
, находящейся на высоте  над уровнем земли. Вектор ск-ти
над уровнем земли. Вектор ск-ти  втекающих частиц жидкости
втекающих частиц жидкости  сечению трубы и по модулю равен
сечению трубы и по модулю равен  . Давление в жидкости при входе в трубу =
. Давление в жидкости при входе в трубу =  . Через сечение 2, площадь
. Через сечение 2, площадь  , нах-ся на высоте
, нах-ся на высоте  над уровнем земли, жидкость вытекает из трубы со ск-тью
над уровнем земли, жидкость вытекает из трубы со ск-тью  по модулю равной
по модулю равной  . Давление жидкости на входе из трубы =
. Давление жидкости на входе из трубы =  .
. или разности уровней
или разности уровней  , приводящей к гидростатическому давлению соответствующего столба жидкости.
, приводящей к гидростатическому давлению соответствующего столба жидкости. через сечение 1 втекает масса жидкости
через сечение 1 втекает масса жидкости  , заполняющая объем цилиндрика, площадью
, заполняющая объем цилиндрика, площадью  . За тот же промежуток времени через сечение 2 вытекает такая же масса жидкости
. За тот же промежуток времени через сечение 2 вытекает такая же масса жидкости  .
.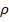 . Получим:
. Получим:  (1).
(1). , получим на основании закона сохранения массы, что для несжимаемой жидкости всегда выполняется простое соотношение между величиной сечения и ск-тью сечения
, получим на основании закона сохранения массы, что для несжимаемой жидкости всегда выполняется простое соотношение между величиной сечения и ск-тью сечения 
 . Эта сила переместила массу жидкости
. Эта сила переместила массу жидкости  .
. сил давления при таком перемешении жидкости равна
сил давления при таком перемешении жидкости равна 
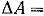
 (2).
(2). , т.к.
, т.к.  , а из ур-ния непрерывности
, а из ур-ния непрерывности  , получим
, получим  (3).
(3). (4)
(4) (5) остается неизменной в любом сечении трубы, т.е. она = const.
(5) остается неизменной в любом сечении трубы, т.е. она = const. представляет удельную кинетическую энергию, т.е. кинетич. эн. единицы объема движущейся жидкости. Величина
представляет удельную кинетическую энергию, т.е. кинетич. эн. единицы объема движущейся жидкости. Величина  - удельная потенц. эн. единицы объема жидкости в поле сил тяжести, в величина p представляет удельную потенц. эн. сил давления в жидкости.
- удельная потенц. эн. единицы объема жидкости в поле сил тяжести, в величина p представляет удельную потенц. эн. сил давления в жидкости.


