
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Торричелли. Ламинарный и турбулентный режимы движения вязкой средыСодержание книги
Поиск на нашем сайте Определим движение частиц жидкости относительно некоторой системы отсчета. В этой сист. отсчета каждой частица соответствует свой вектор ск-ти
Линии тока можно провести через любую точку пр-ва, занятую движущейся жидкостей. Касательная к любой точке линии тока даст нам направление вектора ск-ти. Проведем в пр-ве жидкости какой-либо замкнутый контур.
Если через все точки этого контура провести линии тока, то они образуют пов-ть, называемую трубкой тока. Вектор
В нач. момент времени ур-нь жидкости был на расст H от дна. Жидкость вытекает из открытого сосуда. Поэтому давление
По условию Условие непрерывности Рассмотрим процесс течения жидкости, при небольшой ск-ти течения по трубе жидкость можно разделить на слои, скользящие друг относительно друга. Такое слоистое течение наз. ламинарным. При медленном увеличении ск-ти течения жидкости всегда наступает момент, когда происходит резкий переход от ламинарного течения к движению среды с энергичным перемешиванием, кот. наз. турбулентным (вихревым) движением. Рейнольдс установил, что режим течения среды в трубе зависит от значения величины Переход от ламинарного течения к турбулентному происходит достаточно резко при некотором критическом значении числа Рейнольдса. Число Рейнольдса имеет важное значение и широко используется в моделировании различных типов воздушных судов. Оказывается, что модель самолета, имеющего очень малую величину, или другого тела, ведет себя в аэродинамической трубе точно так же, как и настоящий аппарат в реальных условиях, если для них совпадают числа Рейнольдса. Это позволяет проводить испытания для реальных моделей устройств.
44.Статистический, динамический и термодинамический методы исследования. Любое тело содержит большое кол-во атомов и молекул. Напр, в 1 см3 газа содержится примерно 1020 молекул, а в жидкости и тв. теле примерно 1022 на 1 см3. Если считать, что к каждому атому или молекуле применимы законы Ньютона, то для описания такой системы необходимо составить Статич. метод основан на использовании теории вероятности и определенных моделей строения изучаемых систем. Этот раздел физики наз. статической физикой. В поведении большого числа частиц проявляются закономерности, наз. статич. закономерностями. В системе, состоящей из большого числа частиц, существуют некоторые средние значения физ. величин, хар-ющих всю сов-ть в целом. Напр, средние ск-ти теплового движения молекуд, ср. энергии и т.д. Св-ва системы частиц обусловлены на только индивидуальными св-вами этих частиц, но и особенностями их совокупных движений и средними значениями динамических хар-к частиц. Кроме статистическокго метода исслед. физ. явлений сущ. термодинамический метод, в кот. не учитывается внутреннее строение вещества и характер движения отдельных частиц. Термодинамич. метод основан на изучении различных превращений энергии, происходящих в системе, условий этих превращений и соотношения между разными видами энергии.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

 . Жидкость, состоящая из таких частиц, представляет собой поле вектора ск-ти. Это поле можно наглядно изобразить с помощью линий тока.
. Жидкость, состоящая из таких частиц, представляет собой поле вектора ск-ти. Это поле можно наглядно изобразить с помощью линий тока.

 Определим ск-ть истечения струи несжимаемой жидкости из малого отверстия, находящегося в нижней части сосуда, имеющего форму усеченного конуса при условии
Определим ск-ть истечения струи несжимаемой жидкости из малого отверстия, находящегося в нижней части сосуда, имеющего форму усеченного конуса при условии  .
. сечения
сечения 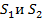 одинаковы и равны атмосферному.
одинаковы и равны атмосферному.  - площадь сечения отверстия. Применим ур-ние Бернулли и ур-ние неразрывности к этим двум сечениям.
- площадь сечения отверстия. Применим ур-ние Бернулли и ур-ние неразрывности к этим двум сечениям.
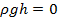 , т.к. это условие для дна сосуда.
, т.к. это условие для дна сосуда.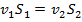 по усл.
по усл.  , тогда
, тогда 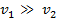 , тогда при вычислении ск-ти
, тогда при вычислении ск-ти  можно пренебречь слагаемым
можно пренебречь слагаемым 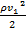 и ск-ть вытекания жидкости
и ск-ть вытекания жидкости  определяется по формуле
определяется по формуле 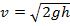 . Эта формула наз. формулой Торричелли. Используя геометрич. и кинематич. соотношения
. Эта формула наз. формулой Торричелли. Используя геометрич. и кинематич. соотношения 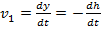 из ур-ния неразрывности
из ур-ния неразрывности 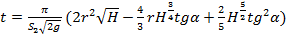 .
.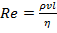 , кот. наз. числом Рейнольдса. Это число явл. безразмерной комбинацией величин: плотности среды
, кот. наз. числом Рейнольдса. Это число явл. безразмерной комбинацией величин: плотности среды 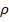 , средней ск-ти
, средней ск-ти 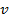 потока по сечению трубопровода, характерного линейного размера
потока по сечению трубопровода, характерного линейного размера 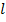 поперечного сечения и коэф-та динамической вязкости.
поперечного сечения и коэф-та динамической вязкости. 1022 динамич. ур-ний. Это сделать невозможно, поэтому макроскопические св-ва, состоящих из очень большого числа частиц, изучаются статистическим методом.
1022 динамич. ур-ний. Это сделать невозможно, поэтому макроскопические св-ва, состоящих из очень большого числа частиц, изучаются статистическим методом.


