
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ур-ние состояния идеальных газовСодержание книги
Поиск на нашем сайте Любое кол-во газа хар-ется след. 4-мя величинами: 1)масса m; 2)занимаемый объем V; 3)давление p; 4)температура t. Запишем наиболее простые эмпирические закономерности для случаев, когда 2(две) из указанных величин явл. const. А)Закон Бойля-Мариотта Для данной массы газа m=const и при постоянной температуре T=const давление газа изменяется обратно пропорционально объему pV=const. (1) Б)Законы Гей-Люссака 1.Давление данной массы газа при постоянном объеме изменяются линейно с температурой 2.Объем данной массы газа при постоянном давлении изменяется линейно с температурой Коэф. Коэф. Если ввести обозначение температуры T = t +273° -> T – 273 = T Введенная шкала температур T наз. шкалой Кельвина. Рассмотрим опред. массу m, которая занимает объем Пусть в другом состоянии так же масса m хар-ся объемом Установим на основании законов Гей-Люссака и Бойля-Мариотта связь между Для перехода от первого состояния ко второму нагреем газ при постоянном давлении до температуры В рез-те этого нагрева газ окажется в состоянии, характеризуемым объемом Подставим в эту формулу значение Из этой формулы следует, что при изменениях состояния данной массы газа величина pV/T остается постоянной pV/T = B (7), где B = const. Если в отношении 7 брать не произвольное кол-во газа, а один моль, то постоянная B будет иметь одно и то же значения для всех газов. Эта постоянная обознач. R и наз. газовой постоянной. Введя в формулу (7) вместо объема V молярный объем Эта формула явл. ур-нием состояния идеального газа и наз. формулой Менделеева-Клапейрона. (моль – единица кол-ва вещества (газа), равная кол-ву вещества (газа) системы, в которой содержится столько же структурных элементов (атомы, молекулы, ионы, электроны…), сколько содержится их в 0,012 кг углерода 12-го). Формулу (8), справедливую лишь для 1 моля газа, можно обобщить на любую массу. Для этого обозначим через M – молекулярный вес газа. Тогда, если при некоторых данных давлений и температуры 1 моль газа занимает объем Отсюда следует, что для m граммов газа при данных давлении и температуре выр. pV/T также будет в m/M раз больше газовой постоянной R. Формула (9) представляет собой обобщение формулы Менделеева-Клапейрона и справедлива для любой массы газа. Молекулы газа, находящиеся в каком-либо сосуде, двигаясь хаотично, сталкиваются со стенками сосуда и оказывают на них давление. Это давление опис. Формулой: Поделив и умножив правую часть ур-ния (1) на 2, получим Величина Ур-ние (11) и эквивалентное ему ур-ние (12) носят название основной формулы кинетич. энергии газов. Умножив левую и правую части ур-ния (12) на объем 1 моля газа Здесь величина С другой стороны мы имеем Формула (13) непосредственно связывает среднюю кинетич. энергию поступат. движ. молекул Из ур-ния (13) мы можем записать Газовая постоянная и число Авогадро – величины постоянные, значит их отношение такде величина постоянная
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (2).
(2). (3)
(3) наз. термическим коэф-том давления.
наз. термическим коэф-том давления. наз. термическим коэф-том объема, причем
наз. термическим коэф-том объема, причем  .
. , где
, где  , то ур-ния (2) и (3) примут вид
, то ур-ния (2) и (3) примут вид 
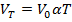 (5).
(5). , имеет давление
, имеет давление  и нах-ся при температуре
и нах-ся при температуре  .
. , давлением
, давлением  и температурой
и температурой 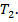
 . При этом процессе газ займет объем
. При этом процессе газ займет объем  , т.е.
, т.е. 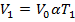 ;
;  . Откуда
. Откуда  (6).
(6). ,
,  .
. (6) и получим
(6) и получим  или
или 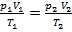 .
. , т.е. объем 1 моля газа, получим формулу
, т.е. объем 1 моля газа, получим формулу  .
. .
.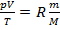 (9).
(9). (10), т.е. давление p, оказываемое газон на стенки сосуда, определяется числом молекул
(10), т.е. давление p, оказываемое газон на стенки сосуда, определяется числом молекул  в единице объема, массой m молекул и средним значением квадрата их ск-тей.
в единице объема, массой m молекул и средним значением квадрата их ск-тей. (11)
(11) есть кинетич. энергия, тогда
есть кинетич. энергия, тогда  (12).
(12). .
. есть число молекул в молярном объеме
есть число молекул в молярном объеме  число Авогадро, тогда
число Авогадро, тогда  .
. (13).
(13). с макроскопическими величинами, характеризующими газ
с макроскопическими величинами, характеризующими газ  .
.
 , где k – постоянная Больцмана.
, где k – постоянная Больцмана.


