
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Траектория и путь м.т. Ск-ть м.т.Содержание книги
Поиск на нашем сайте Введение Простейший вид движ. в прир. - мех. движ., состоящее в изменении взаимного располож. тел или их частей в пр-ве с теч. времени. Мех-ка – раздел физ., занимающийся изучением закономерности мех. движ. Если движ. макроскопич. тел совершается со скоростями во много раз меньше ск-ти света в вакууме, то такая мех-ка наз. классич., или Ньютоновской, т.к. в основе класс. мех. лежат законы Ньютона. Закономерности движ. тел со скоростями, близкими к v света в вакууме, явл. предметом релятивистской мех-ки. Законы движ. микрочастиц (электронов в атомах, молекулах, кристаллах) явл. предметом квантовой мех-ки. Класс. мех-ка сост. из 3 осн. разделов: 1)статики; 2)кинематики; 3)динамики В статике рассм. законы сложения сил и условия равновесия тел. В кинематике дается матем. описание всевозможных видов движ. без рассмотрения причин, обеспечивающих появление каждого конкретного вида движ. В динамике изучается влияние взаимодействия между телами на их мех. движение. При описании реального движ. тел в мех-ке используют упрощенные модели, напр. матер. точка(м.т.), абс. тв. тело, абс. упругое тело и др. М.т. наз. тело, размеры и форма которого несущественны в условиях данной задачи. Любое протяженное тело или сист. таких тел, образующих исследуемую сист., можно рассм. как сист. м.т. Для этого необходимо протяженное тело разбить на сист. м.т. пренебрежимо малых по сравнению с размерами самих тел. Для описания любого тела наблюдатель должен выбрать сист. отсчета, под кот. понимают тело отсчета, реальное или воображаемое, и связанную с ним сист. коорд., а также опред. способ измерения времени. (Рис.)
Это позволяет наблюдателю устанавливать положение изуч. объекта М(м.т.) по отношениию к сист. отсч. в любой момент t. Выбор сист. коорд. произволен и определяется условиями задачи. Для описания движ. м.т. использ. 3 способа задания движения: векторный, координатный, естественный, или траекторный. При вект. способе - на теле отсчета выбирается т.О – начало отсчета, из кот. в направлении движущейся т.М проводят радиус-вектор (Рис.)
При движении т.М модуль и направления Если вид ф-и Закон движ. м.т. в вект. форме имеет вид В случае коорд. способа - с телом отсчета связывают сист. коорд., позволяющую каждой точке пространства сопоставить 3 числа, кот. наз. координатами точки. Наиб. распространенной явл. прямоуг. декарт. сист. коорд. В ПДСК положение матер. т.М определяется 3-мя коорд. – x, y, z. При движении точки эти коорд. применяются во времени и движение точки описывается 3-мя параметрическими(кинетич.) ур-ниями. x = x(t), y = y(t), z = z(t). (Рис.)
Где Параметрич. ур-ния представляют собой коорд. форму записи закона движ. точки. Если т. движется по плоскости, то остаются 2 ур-ния, если движ. в одном направлении – одно. В различных сист. отсчета законы движ. одной и той же м.т. имеют различный вид. Любое свободное тело, не подвергающееся внешним воздействиями, не может нах-ся в состоянии покоя, но всегда можно найти такую сист. отсчета, по отношению к кот. пр-во явл. однородным и изотропным, а время однородным. Такая сист. отсчета наз. инерциальной. В инерц. сист. отсчета всякое свободное движ. происходит с постоянной по величине и направлению скоростью. Этот вывод явл. содержанием 1-го зак. Ньютона, кот. гласит: всякое свободное тело нах-ся в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Если наряду с имеющейся у нас инерц. сист. отсчета ввести другую сист. отсчета, движущуюся относительно первой прямолинейно и равномерно, то законы свободного движения в этой новой сист. будут теми же, что и по отношению к первоначальной сист. Это говорит о том, что сущ. не одна, а бесконечное мн-во инерц. сист. отсчета, связанных с м.т-ми и движ друг относит друга прямолин. и равномерн. Ускорение м.т. Для хар-ки быстроты изменения ск-ти точки в мех-ке вводится понятие ускорение. Средним ускорением точки в интервале времени от t до t+∆t наз. вектор Ускорением, или мгновенным ускорением наз. вект. величина Ускор. т. в мом. врем.t = пределу средн. ускор. Разложение вектора Модуль вектора ускорения | Вектор ускор. м.т. лежит в соприкасающейся плоскости в проведенной т.М траектории и направлен в сторону вогнутости траектории ВС. (Рис).
В этой плоскости вектор ускорения a можно разложить на 2 взаимно Составляющая В общ. случае траектория точки представляет собой не плоскую, а пространственную кривую. Для такой кривой вводится понятие соприкасающейся плоскости. Соприкасающейся плоскостью в произвольной т.М кривой наз. предельное положение плоскости, проходящей через любые 3 точки кривой, когда эти точки неограниченно приближаются к т.М. Составляющая
Сила Силой наз. вект. величина, являющаяся мерой мех. действия на рассматриваемое тело со стороны других тел. Мех. взаимодействие может осущ. как между непосредственно контактирующими телами посредством трения, давления и т.д., так и между удаленными телами. Форма материи, связывающая частицы вещества в единые системы и передающая с конечной ск-тью действия одних частиц на другие, наз. физ. полем, или просто полем. Взаимодействие между удаленными телами осущ. посредством создаваемых ими гравитационных или электромагнитных полей. Мех. действие на данное тело со стороны других тел проявляется двояко: оно способно вызывать: 1)изменение состояния мех. движения рассматриваемого тела. 2)его деформацию. Сила Прямая, вдоль кот. направлена сила, наз. линией действия силы. Поле, действующее на м.т. с силой Одновременное действие на м.т. М нескольких сил
Масса и Импульс тела В класс. Ньютоновской мех-ке массой матер. т. наз-ся полож-ая, скалярн. величина, яв-ся мерой инертности этой точки. Под действием силы мат.т. изменяет свою скорость не мгновенно, а постепенно, т.е. приобр. Конечное по величине ускор-е, кот. тем меньше, чем больше масса мат.т. Для сравн. масс m1 и m2 2-х мат.т. достаточно измерить модули a1 и a2 приобретенными этими т. Под действием одной и той же силы F.
В класс. Ньют. мех-ки считается, что: 1) масса мат.т. не зависит от состояния движ-я т., явл-ся ее неизмен-ой хар-кой. 2) масса величина одитивная, т.е. масса ситемы равна сумме всех мат.т. вход. в состав этой сист. 3) масса замкн. сист. Остается неизмен. при любых процессах, происх. в этой сист. Векторная величина 2 закон Ньютона: Динамическое ур-е 2-го закона Ньютона:
Ускорение мат.т. совпадает по напр-нию с действ. на нее силой и равно отношению этой силы к массе мат.т.
При криволин. движ. тангексальное и центр. уск-е мат.т. опред. соотв. сост. силы F.
ДУ движ-я мат.т. наз-ся ур-е
В проекц. на оси декарт.сист.коорд это динамическое ур-е имеет вид: 3 закон Ньютона Силы с кот-ми взаимодействуют 2 мат.т равны по модулю, противоположны по напр-ию и направлены вдоль прямой, соед. эти точки.
Из 3-го закона следует что в любой замкнутой механ. сист. геометр. сумма всех внутр. сил равны нулю
Вектор , действ.на сист., наз-ся главным вектором внешн. сил.
Исп. 2-ой закон Ньютона:
Центр масс Если сист. сост. из N м.т., то в этом случае вводится понятие центра масс. Центром масс сист. м.т. наз. т.С, положение кот. опред. радиус-вектором В проекциях на ПДСК координата центра масс запишется Центр масс(центр инерции) сист. м.т. совпадает в однородном поле силы тяжести с центром тяжести системы. Ск-ть центра масс запишется формулой Согласно ур-нию (1) суммарный импульс сист. м.т. можно представить в вилле произведения массы системы на ск-ть центра масс. Тогда ур-ние движения центра масс запишется в виде Если изучаемая сист. явл. тв. телом, движущимся поступательно, то ск-ть
Закон сохранения импульса Рассм. сист., состоящую из N матер. точек. Обозначим через Символом
Где Чтобы получить ур-ние движения такой сист., мы должны суммировать все силы, действующие как внутри сист., так и на сист., тогда левая часть этой суммы есть производная по t от суммарного импульса сист. Правая часть содержит ∑ всех внутренних действующих в сист. сил и сумму внешних сил, действующих на сист. Согласно 3-му з.Ньютона, результирующая всех внутр. сил = 0, т.к. каждая сумма сил в скобке = 0, т.е Учитывая, что рав-во для суммарного импульса мы можем записать В этой сумме правая часть есть сумма всех внешних сил, т.е. производная по времени от суммарного импульса сист. = сумме внешних сил, действующих на тела системы. Если сист. замкнута(консервативна), то внешние силы отсутствуют, сумму всех Такое выр. указывает, что В отличие от законов Ньютона, закон сохр. импульса принадлежит к числу фундаментальных физ. законов. Он связан с определенным св-вом симметрии пр-ва, его однородностью, кот. проявляется в том, что физ. св-ва замкнутой сист. и законы ее движения не зависят от выбора положения начала координат инерциальной сист. отсчета, т.е. эти законы не изменяются при || переносе в пр-ве замкнутой сист. как целого.
Движение тела перем. массы В Ньютоновской мех-ке масса тела может изменяться в незамкнутой системе только в рез-те отделения от тела или присоединения к нему частиц вещества(прим: ракета). В процессе полета масса ракеты постепенно уменьшается. Ур-ние поступат. движ. тела перем. массы, или ур-ние Мещерского, запишется в виде:
Ур-ние Мещерского отличается от 2-го зак.Ньютона доп. членом Реактивная сила хар-ет мех. действие на тело отделяющихся либо присоединяющихся к нему частиц. Ур-ние движения ракеты в отсутствие внешн. сил записывается в виде: Если нач. ск-ть ракеты =0 в момент старта, то ракета движется прямолинейно в направлении, противоположном относительно ск-ти Max ск-ть, кот. может развить ракета в отсутствии внешних сил, наз. характеристической ск-тью. Эта ск-ть достигается в момент работы двигателя, когда иссяк весь запас топлива. Влияние тяготения земле и сопротивления воздуха (т.е внешние силы Хар-кая ск-ть составной многоступенчатой ракеты опред. формулой: Увеличения хар-кой ск-ти многоступ. ракеты происходит за счет последовательного уменьшения ее массы, за счет отделения от нее ступеней ракеты.
Момент силы Для хар-ки внешнего мех. воздействия на тело, приводящее к изменению его вращательного движения, вводят понятие момента силы.
Направление Модуль момента силы: Проекция
Момент импульса а) моментом импульса, или моментом кол-ва движения м.т. относит. неподвижной т.О (полюса), наз. б) моментом импульса сист. м.т-ек относительно неподвижной т.О наз. сумма Модуль моменты импульса запишется как модуль вект. произвед.
Момент инерции
Мом. инерц. тв. тела относит. оси ОО’ запис. формулой. Если тело однородное, то плотность его во всех т. Одинаковая и = const и ее можно вынести за знак интеграла.
Рассм. произвольное тело и 2 || друг другу оси, одна из кот. – ось С проходит через центр масс тела, а другая – ось О - || оси С и отстоит от нее на расстояние l. Выберем оси координат как показано на рис. Момент инерции I относит. оси О опред. выр. Первая сумма в () дает координаты точки массой Во вторую сумму входит сумма координат В третьей сумме Учитывая т.Штейнера, вводятся след. физ. понятия: 1)оси инерции, проходящие через центр инерции тела (центр масс), наз. главными центральными осями инерции тела, а момент инерции тела относительно этих осей – главными центральными моментами инерции. 2)Ось симметрии однородного тела всегда явл. одной из его главных центральных осей инерции.
Энергия Энергией наз. скал. Физ. величина, явл-ся общей мерой различных форм движения материи, рассматриваемых в физике. Эн. Сист. количественно хар-ет эту сист. в отношении возможных в ней превращений движения. Эти превращения происходят благодаря взаимодействию частей системы как друг с другом, так и с внешними телами, внешней средой. Для анализа качественно различных форм движения и соответствующих сил взаимодействий в физике вводят различные типы энергии – механич., электромагнитн., ядерную и др. Изменение мех. движения тела вызывается силами, действующими на него со стороны других тел. Для количественного описания такого процесса обмена энергией между взаимодействующими телами в мех-ке пользуются понятием работы силы, приложенной к рассматриваемому телу. Мех. эн. Бывает 2-х видов: -кинетическая -потенциальная. Кинетическая эн. опред. массами и скоростями рассматриваемых тел. Потенциальная эн. зависит от взаимного расположения взаимодействующих друг с другом тел.
Колебание. Типы колебаний Колебаниями наз. движения или процессы, обладающие то или иной повторяемостью во времени. Колебания м.б. разной природы. В класс. физике рассм. механические, электромагн. и электромех. колебания. В зависимости от характера воздействия на колеблющуюся сист. различают: свободные, или собственные колеб.; автоколеб. и параметрические колебания. Свободными наз. колеб., кот. происходят в отсутствие внешних переменных воздействий на колебат. сист. и возникают вследствие какого-либо начального отклонения этой сист. от состояния ее устойчивого равновесия. Вынужденными наз. колеб., возникающие в какой-либо системе под влиянием переменного внешнего воздействия. Автоколебаниями наз. колеб., кот. задается внешней силой, а сама система, на кот. действует эта сила, управляет этой внешней силой. Параметрические - колеб, кот. происходят за счет внешних сил, периодически изменяющих какой-либо параметр системы (напр. изменение длины нити маятника). Колеб. наз. периодич., если значения всех физ. величин, хар-щих колеб. Систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени. Наименьший промежуток времени Т, удовлетворяющий этому условию, наз. периодом колебаний. За период колеб. Т система совершает одно полное колебание. Частотой периодич. колебаний наз. величина Циклической, или круговой частотой, периодич. колеб. наз. величина
Гармонические колебания При периодич. колеб. зависимость колеблющейся величины S от времени t удовлетворяет условию S(t+T)=S(t). Периодич. колеб. величины S(t) наз. гармоническими колебаниями, если величина S(t) совершает колебания по закону синуса или косинуса. Значение S(t) в произвольный момент времени t опред. значением фазы колебаний Ф(t)= Запишем гармонич. колебание в виде уравнения S(t)=Asin( Начальная фаза скорости = Начальная фаза ускорения равна
Если гармонически колеблющаяся величина Общее реш. этого ДУ приводится к стандартному виду гармонич. колеб.
Метод вект. диаграмм Гармонич. колеб. можно изобразить графически в виде вектора на плоскости. Для этого из нач. коорд. т.О на плоскости проводят вектор Графическое изображение гармонич. колебаний посредствам вращающегося вектора амплитуды наз. методом векторных диаграмм. Этим методом широко пользуются при сложении одинаково направленных гармонич. колеб.
Сферическая и стоячие волны Волна наз. сферич., если ее волновые пов-ти имеют вид концентрических сфер. Центр этих сфер наз. центром волны. Ур-ние расходящ. сферич. волны имеет вид Ур-ние синусоид. сферич. волны: Распространение плоской и расходящейся сферических волн в однородной изотропной среде описывается ДУ частных производных, кот. наз. волновым ур-нием Скорость Для плоской синусоид. волны мы имеем выражение для фазы Продиф-ем это выр. один раз по t и по x.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |

 .
. изменяется, т.е. он явл. ф-ей времени.
изменяется, т.е. он явл. ф-ей времени. известен, то ур-ние движ. т.М задано в вект виде. Конец
известен, то ур-ние движ. т.М задано в вект виде. Конец  , где
, где  единичный вектор в направлении
единичный вектор в направлении  единичн. Векторы соотв. коорд. осей.
единичн. Векторы соотв. коорд. осей. = отношению приращения
= отношению приращения 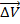 точки за время ∆t.
точки за время ∆t.  .
.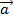 , равная 1-й произв. по врем. от ск-ти
, равная 1-й произв. по врем. от ск-ти  рассм. точки или 2-й произв. по врем. от
рассм. точки или 2-й произв. по врем. от  .
. при неограниченном уменьшении продолжительности интервала ∆t:
при неограниченном уменьшении продолжительности интервала ∆t:  .
. по базису ПДСК. Проекции ускор. на оси коорд. = 1-м произв. по врем.
по базису ПДСК. Проекции ускор. на оси коорд. = 1-м произв. по врем. 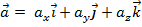 от соотв. проекций ск-ти, и 2-м произв. по врем. от соотв. коорд-т точки
от соотв. проекций ск-ти, и 2-м произв. по врем. от соотв. коорд-т точки 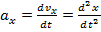 ,
,  ,
, 
 =
=  .
. составляющих
составляющих  и
и  :
: 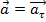 +
+ 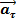 , направленная по касательной к траектории, наз. тангенциальным ускорен точки
, направленная по касательной к траектории, наз. тангенциальным ускорен точки  , где
, где  единичный вектор.
единичный вектор.  ,
,  -проекция касательного ускорения на направление вектора
-проекция касательного ускорения на направление вектора  движение наз. равномерный.
движение наз. равномерный. ускорения a м.т. наз. ее нормальным ускорением. Эта составляющая направлена по главной нормали траектории в т.М в сторону к центру кривизны траектории. Поэтому часто
ускорения a м.т. наз. ее нормальным ускорением. Эта составляющая направлена по главной нормали траектории в т.М в сторону к центру кривизны траектории. Поэтому часто 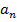 наз. центростремительным ускорением.
наз. центростремительным ускорением.  , где
, где  - единичный вектор нормали,
- единичный вектор нормали, 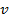 – лин. ск-ть м.т.,
– лин. ск-ть м.т.,  – радиус кривизны траектории в т.М.
– радиус кривизны траектории в т.М. полностью определена, если заданы ее модуль, направление в пр-ве и точка приложения.
полностью определена, если заданы ее модуль, направление в пр-ве и точка приложения. , наз. стационарным полем, если оно не изменяется с теч. времени t
, наз. стационарным полем, если оно не изменяется с теч. времени t 
 ,
,  …
…  эквивалентно действию одной силы, называемой равнодействующей, или результирующей силой, и равной вект. сумме всех действующих сил
эквивалентно действию одной силы, называемой равнодействующей, или результирующей силой, и равной вект. сумме всех действующих сил 
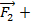 …+
…+  =
= 

 = произв. масс
= произв. масс  на
на  наз-ся импульсом или кол-ом движения этой мат.т.
наз-ся импульсом или кол-ом движения этой мат.т. , сумме сил, действ. на данную мат.т.
, сумме сил, действ. на данную мат.т.
 или исп. ур-е импульса:
или исп. ур-е импульса:  , т.к. m=const:
, т.к. m=const:  ;
; .
.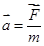
 ;
; ;
;
 ,
,  ,
,  .
.

 ,т.е. век-р всех внешних сил, равный геомтр. сумме всех внешн.сил
,т.е. век-р всех внешних сил, равный геомтр. сумме всех внешн.сил
 эта формула выражает з-н изменения импульса сист.
эта формула выражает з-н изменения импульса сист.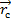 , кот.
, кот.  , где
, где 
 масса и радиус-вектор i-той м.т. N-общее число м.т-ек в сист.,
масса и радиус-вектор i-той м.т. N-общее число м.т-ек в сист.,  – масса всей системы.
– масса всей системы. ;
;  .
. (1). Где
(1). Где  - импульс системы.
- импульс системы.
 , где m – масса системы,
, где m – масса системы,  - ускорение центра масс.
- ускорение центра масс. точек тела и ск-ть центра масс
точек тела и ск-ть центра масс  одинаковы и равны
одинаковы и равны  (
( ) и основное ур-ние динамики поступат. движ. тв. тела имеет вид
) и основное ур-ние динамики поступат. движ. тв. тела имеет вид  .
. силу, с кот. k-я м.т. действует на i-ю.
силу, с кот. k-я м.т. действует на i-ю.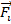 обозначим результирующую всех внешних сил, действующих на i-ю частицу. Тогда динамическое ур-ние движ. запишется в виде
обозначим результирующую всех внешних сил, действующих на i-ю частицу. Тогда динамическое ур-ние движ. запишется в виде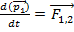 +
+  …+
…+  +
+  +
+  …+
…+  +
+ 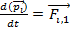 +
+  …+
…+  – импульс i-й частицы,
– импульс i-й частицы, 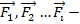 внешние силы, действующие на м.т.
внешние силы, действующие на м.т.
 .
. (1).
(1). , то в ур-нии (1) правая часть = 0.
, то в ур-нии (1) правая часть = 0. 
 и закон сохр. импульса сформулируется след. образом: суммарный импульс замкнутой сист. м.т. остается постоянным.
и закон сохр. импульса сформулируется след. образом: суммарный импульс замкнутой сист. м.т. остается постоянным. где
где  и
и 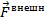 - главный вектор внешних сил, действующих на тело,
- главный вектор внешних сил, действующих на тело,  - ск-ть частиц после отделения от тела, если
- ск-ть частиц после отделения от тела, если  , или ск-ть присоединения, если
, или ск-ть присоединения, если 
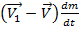 . Этот доп. член правой части ур-ния представляет собой доп. силу, действующую на тело переменной массы. Эта сила наз. реактивной силой
. Этот доп. член правой части ур-ния представляет собой доп. силу, действующую на тело переменной массы. Эта сила наз. реактивной силой  где
где 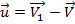 - ск-ть отделяющихся либо присоединяющихся частиц, т.е. их ск-ть по отношению к сист. отсчета, движущаяся поступательно вместе с телом, напр. ракетой.
- ск-ть отделяющихся либо присоединяющихся частиц, т.е. их ск-ть по отношению к сист. отсчета, движущаяся поступательно вместе с телом, напр. ракетой.
 струи газа. В этом случае
струи газа. В этом случае  и при
и при 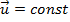 связь между ск-тью ракеты и ее массой по модулю выражается формулой Циалковского
связь между ск-тью ракеты и ее массой по модулю выражается формулой Циалковского  , где
, где  – начальная, стартовая масса ракеты с топливом и окислителем.
– начальная, стартовая масса ракеты с топливом и окислителем. где
где 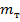 - начальная масса топлива и окислителя.
- начальная масса топлива и окислителя. где n – общее число ступеней ракеты;
где n – общее число ступеней ракеты;  - масса топлива и окислителя, предназначенных для работы i-той ступени;
- масса топлива и окислителя, предназначенных для работы i-той ступени; 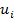 - cr-nm истечения газов i-той ступени;
- cr-nm истечения газов i-той ступени;  Моментом силы
Моментом силы  , равная вект. произведению
, равная вект. произведению 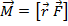 .
. производить вращение по наименьшему углу в направлении силы
производить вращение по наименьшему углу в направлении силы  ), α=
), α=  где α – наим. угол между векторами
где α – наим. угол между векторами  – длина перпендикуляра ОВ, опущенного из т.О на линию действия силы, где
– длина перпендикуляра ОВ, опущенного из т.О на линию действия силы, где 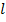 – наз-ся плечом силы относительно т.О. когда
– наз-ся плечом силы относительно т.О. когда  хар-ет способность силы вращать тело вокруг т.О, относит. кот. берется этот момент силы.
хар-ет способность силы вращать тело вокруг т.О, относит. кот. берется этот момент силы.
 , равный вект. произвед.
, равный вект. произвед.  проведенного из полюса О в место нахождения м.т., на вектор
проведенного из полюса О в место нахождения м.т., на вектор  импульса этой точки.
импульса этой точки.  , где
, где  - масса и ск-ть м.т.
- масса и ск-ть м.т. , где
, где  - масса, радиус-вектор и ск-ть i-той м.т., n – общее число этих точек в системе.
- масса, радиус-вектор и ск-ть i-той м.т., n – общее число этих точек в системе. . Если частица движется прямолинейно, то момент импульса может изменяться только за счет изменения модуля вектора ск-ти.
. Если частица движется прямолинейно, то момент импульса может изменяться только за счет изменения модуля вектора ск-ти. Мом. инерции мех. сист. относит. неподвижн. оси ОО’ наз. физ. величина I0 = сумме произведений масс всех N м.т-ек сист. на квадрат из расстояния до этой оси.
Мом. инерции мех. сист. относит. неподвижн. оси ОО’ наз. физ. величина I0 = сумме произведений масс всех N м.т-ек сист. на квадрат из расстояния до этой оси. , где
, где  и
и 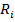 - масса м.т. и ее расстояние до оси.
- масса м.т. и ее расстояние до оси. (1), где
(1), где  - масса малого элемента тела
- масса малого элемента тела  ,
, 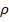 - плотность тв. тела, R – расстояние от элемента объема
- плотность тв. тела, R – расстояние от элемента объема  (2).
(2). Если тело оси симметричное, то можно опред. мом. инерц. такого тв. тела относительно любой оси, || -ной данной.
Если тело оси симметричное, то можно опред. мом. инерц. такого тв. тела относительно любой оси, || -ной данной.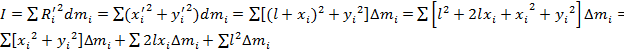
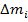 относительно центра тяжести, в произведение под суммой дает произведение Ic относительно центра масс
относительно центра тяжести, в произведение под суммой дает произведение Ic относительно центра масс , кот. =
, кот. =  всех
всех  мы имеем
мы имеем  , а это есть масса нашего тела. Тогда момент инерции тела относительно оси О, находящейся на расстоянии l от оси С, проходящей через центр масс и || оси О, запишется ур-нием
, а это есть масса нашего тела. Тогда момент инерции тела относительно оси О, находящейся на расстоянии l от оси С, проходящей через центр масс и || оси О, запишется ур-нием  . Это ур-ние наз. т.Штейнера, или т. о переносе осей симметрии. Это теор. формулируется так: момент инерции тела относительно произвольной оси (О) равен сумме моментов инерции относительно оси, || данной и проходящей через центр масс тела, и произведения массы m тела на квадрат расстояния между осями.
. Это ур-ние наз. т.Штейнера, или т. о переносе осей симметрии. Это теор. формулируется так: момент инерции тела относительно произвольной оси (О) равен сумме моментов инерции относительно оси, || данной и проходящей через центр масс тела, и произведения массы m тела на квадрат расстояния между осями.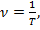 равная числу полных колебаний, совершающихся за единицу времени.
равная числу полных колебаний, совершающихся за единицу времени.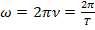 и равная числу полных колебаний, совершаемых за
и равная числу полных колебаний, совершаемых за  единиц времени.
единиц времени.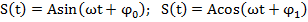 , где величина A = Smax=const >0 есть мах значение колеблющ. величины S и наз. амплитудой коелбаний,
, где величина A = Smax=const >0 есть мах значение колеблющ. величины S и наз. амплитудой коелбаний,  и
и 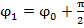 постоянные величины.
постоянные величины.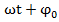 ; Ф1(t)=
; Ф1(t)= 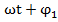 величин
величин 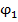 представляют собой начальные фазы колебаний, т.е. значение Ф(t) и Ф1(t) в момент времени t=0 начала отсчета времени
представляют собой начальные фазы колебаний, т.е. значение Ф(t) и Ф1(t) в момент времени t=0 начала отсчета времени 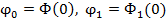 .
.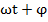 ), где S(t) – величина смешения м.т. из положения равновесия, тогда 1-я и 2-я произв., т.е v и a колеблющегося тела запишется в виде формулы
), где S(t) – величина смешения м.т. из положения равновесия, тогда 1-я и 2-я произв., т.е v и a колеблющегося тела запишется в виде формулы 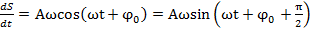 ;
; 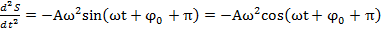 , причем амплитуды скорости и ускорения соответственной равны
, причем амплитуды скорости и ускорения соответственной равны 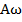 и
и 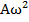 .
.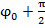 , т.е разность фаз колебаний скорости и смешение S(t) постоянны и =
, т.е разность фаз колебаний скорости и смешение S(t) постоянны и =  . Это значит, что величина
. Это значит, что величина 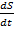 опережает S(t) по фазе на
опережает S(t) по фазе на 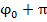 , т.е. разность фаз. Колебаний ускорения и S(t) постоянна и =
, т.е. разность фаз. Колебаний ускорения и S(t) постоянна и = 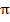 .
.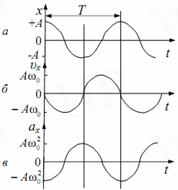 Графики зависимости величин S (а),
Графики зависимости величин S (а), 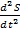 (в) для гармонических колебаний в случае
(в) для гармонических колебаний в случае 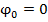 показаны на рис. (S(t)=Acos….).
показаны на рис. (S(t)=Acos….). ,
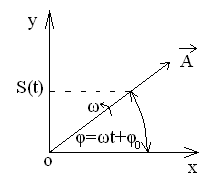
,  , то гармонически колеблющаяся величина S(t) удовлетворяет ДУ типа
, то гармонически колеблющаяся величина S(t) удовлетворяет ДУ типа 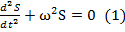 .
.
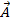 , модуль кот. = амплитуде A рассматриваемых колебаний и составляет с осью координат Ох угол
, модуль кот. = амплитуде A рассматриваемых колебаний и составляет с осью координат Ох угол 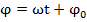 , т.е. = фазе колебаний в данный момент времени. С теч. времени t угол
, т.е. = фазе колебаний в данный момент времени. С теч. времени t угол 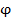 увелич. так, что вектор
увелич. так, что вектор 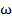 . Тогда проекция
. Тогда проекция 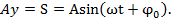
 , где
, где  – расстояние от центра волны до рассматриваемой т.М среды;
– расстояние от центра волны до рассматриваемой т.М среды;  , где
, где  – амплитуда волны;
– амплитуда волны;  - физ. величина, численно равная амплитуде волны на единичном расстоянии от ее центра;
- физ. величина, численно равная амплитуде волны на единичном расстоянии от ее центра;  - нач. фаза колебаний в центре волны.
- нач. фаза колебаний в центре волны. или
или  , где
, где 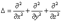 и наз. оператором Лапласа скалярного поля.;
и наз. оператором Лапласа скалярного поля.;  – физ. величина, кот. хар-ет возмущение, распространяющееся в среде со скоростью
– физ. величина, кот. хар-ет возмущение, распространяющееся в среде со скоростью  .
. т.к.
т.к. 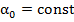 .
. 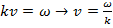 , т.е. фазовая ск-ть связана с циклич
, т.е. фазовая ск-ть связана с циклич 


