
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступат. и вращат. движ. тв. тела.Содержание книги
Поиск на нашем сайте Поступат. движ. тв. тела наз. такое его движ., при кот. любая прямая, жестко связанная с телом, перемещается, оставаясь || своему первонач. положению. При поступат. движ. тв. тела все его точки перемещаются совершенно одинаково, т.е. за малое время ∆t радиус-векторы этих точек изменяются на одну и ту же величину
Положение тела в пр-ве при вращении полностью опред. значением угла поворота Хар-кой быстроты и направления вращения тела вокруг оси служит угловая ск-ть. Угл. ск-тью наз. По величине
Движение тв. тела, при кот. одна из его точек остается неподвижной, наз. вращением тела вокруг неподвижной точки. Обычно эту точку выбирают за начало неподвижной сист. коорд. При вращении вокруг неподвижной точки все точки тела движутся по поверхности концентрических сфер, центры кот. нах-ся в неподвижной точке. В каждый ∞ малый промежуток времени это движение тела можно рассм. как вращение вокруг некоторой оси, проходящей через неподвижную точку. Эта ось наз. мгновенной осью вращения. Для хар-ки быстроты изменения вектора угловой ск-ти тела при неравномерном вращении тела вокруг неподвижн. оси или неподвижн. точки вводится вектор Когда тело вращ. вокруг неподвижy. оси, то этот вект. а)в ту же сторону, что и б)в противоположную сторону при замедленном вращении. Проекция угл. Ускорения на неподвижную ось вращения Oz =
Сила Силой наз. вект. величина, являющаяся мерой мех. действия на рассматриваемое тело со стороны других тел. Мех. взаимодействие может осущ. как между непосредственно контактирующими телами посредством трения, давления и т.д., так и между удаленными телами. Форма материи, связывающая частицы вещества в единые системы и передающая с конечной ск-тью действия одних частиц на другие, наз. физ. полем, или просто полем. Взаимодействие между удаленными телами осущ. посредством создаваемых ими гравитационных или электромагнитных полей. Мех. действие на данное тело со стороны других тел проявляется двояко: оно способно вызывать: 1)изменение состояния мех. движения рассматриваемого тела. 2)его деформацию. Сила Прямая, вдоль кот. направлена сила, наз. линией действия силы. Поле, действующее на м.т. с силой Одновременное действие на м.т. М нескольких сил
Масса и Импульс тела В класс. Ньютоновской мех-ке массой матер. т. наз-ся полож-ая, скалярн. величина, яв-ся мерой инертности этой точки. Под действием силы мат.т. изменяет свою скорость не мгновенно, а постепенно, т.е. приобр. Конечное по величине ускор-е, кот. тем меньше, чем больше масса мат.т. Для сравн. масс m1 и m2 2-х мат.т. достаточно измерить модули a1 и a2 приобретенными этими т. Под действием одной и той же силы F.
В класс. Ньют. мех-ки считается, что: 1) масса мат.т. не зависит от состояния движ-я т., явл-ся ее неизмен-ой хар-кой. 2) масса величина одитивная, т.е. масса ситемы равна сумме всех мат.т. вход. в состав этой сист. 3) масса замкн. сист. Остается неизмен. при любых процессах, происх. в этой сист. Векторная величина 2 закон Ньютона: Динамическое ур-е 2-го закона Ньютона:
Ускорение мат.т. совпадает по напр-нию с действ. на нее силой и равно отношению этой силы к массе мат.т.
При криволин. движ. тангексальное и центр. уск-е мат.т. опред. соотв. сост. силы F.
ДУ движ-я мат.т. наз-ся ур-е
В проекц. на оси декарт.сист.коорд это динамическое ур-е имеет вид: 3 закон Ньютона Силы с кот-ми взаимодействуют 2 мат.т равны по модулю, противоположны по напр-ию и направлены вдоль прямой, соед. эти точки.
Из 3-го закона следует что в любой замкнутой механ. сист. геометр. сумма всех внутр. сил равны нулю
Вектор , действ.на сист., наз-ся главным вектором внешн. сил.
Исп. 2-ой закон Ньютона:
Центр масс Если сист. сост. из N м.т., то в этом случае вводится понятие центра масс. Центром масс сист. м.т. наз. т.С, положение кот. опред. радиус-вектором В проекциях на ПДСК координата центра масс запишется Центр масс(центр инерции) сист. м.т. совпадает в однородном поле силы тяжести с центром тяжести системы. Ск-ть центра масс запишется формулой Согласно ур-нию (1) суммарный импульс сист. м.т. можно представить в вилле произведения массы системы на ск-ть центра масс. Тогда ур-ние движения центра масс запишется в виде Если изучаемая сист. явл. тв. телом, движущимся поступательно, то ск-ть
Закон сохранения импульса Рассм. сист., состоящую из N матер. точек. Обозначим через Символом
Где Чтобы получить ур-ние движения такой сист., мы должны суммировать все силы, действующие как внутри сист., так и на сист., тогда левая часть этой суммы есть производная по t от суммарного импульса сист. Правая часть содержит ∑ всех внутренних действующих в сист. сил и сумму внешних сил, действующих на сист. Согласно 3-му з.Ньютона, результирующая всех внутр. сил = 0, т.к. каждая сумма сил в скобке = 0, т.е Учитывая, что рав-во для суммарного импульса мы можем записать В этой сумме правая часть есть сумма всех внешних сил, т.е. производная по времени от суммарного импульса сист. = сумме внешних сил, действующих на тела системы. Если сист. замкнута(консервативна), то внешние силы отсутствуют, сумму всех Такое выр. указывает, что В отличие от законов Ньютона, закон сохр. импульса принадлежит к числу фундаментальных физ. законов. Он связан с определенным св-вом симметрии пр-ва, его однородностью, кот. проявляется в том, что физ. св-ва замкнутой сист. и законы ее движения не зависят от выбора положения начала координат инерциальной сист. отсчета, т.е. эти законы не изменяются при || переносе в пр-ве замкнутой сист. как целого.
Движение тела перем. массы В Ньютоновской мех-ке масса тела может изменяться в незамкнутой системе только в рез-те отделения от тела или присоединения к нему частиц вещества(прим: ракета). В процессе полета масса ракеты постепенно уменьшается. Ур-ние поступат. движ. тела перем. массы, или ур-ние Мещерского, запишется в виде:
Ур-ние Мещерского отличается от 2-го зак.Ньютона доп. членом Реактивная сила хар-ет мех. действие на тело отделяющихся либо присоединяющихся к нему частиц. Ур-ние движения ракеты в отсутствие внешн. сил записывается в виде: Если нач. ск-ть ракеты =0 в момент старта, то ракета движется прямолинейно в направлении, противоположном относительно ск-ти Max ск-ть, кот. может развить ракета в отсутствии внешних сил, наз. характеристической ск-тью. Эта ск-ть достигается в момент работы двигателя, когда иссяк весь запас топлива. Влияние тяготения земле и сопротивления воздуха (т.е внешние силы Хар-кая ск-ть составной многоступенчатой ракеты опред. формулой: Увеличения хар-кой ск-ти многоступ. ракеты происходит за счет последовательного уменьшения ее массы, за счет отделения от нее ступеней ракеты.
Момент силы Для хар-ки внешнего мех. воздействия на тело, приводящее к изменению его вращательного движения, вводят понятие момента силы.
Направление Модуль момента силы: Проекция
Момент импульса а) моментом импульса, или моментом кол-ва движения м.т. относит. неподвижной т.О (полюса), наз. б) моментом импульса сист. м.т-ек относительно неподвижной т.О наз. сумма Модуль моменты импульса запишется как модуль вект. произвед.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |

 .
. Движение тв. тела, при кот. 2 его точки A и B остаются неподвижными, наз. вращением тела вокруг неподвижной оси.
Движение тв. тела, при кот. 2 его точки A и B остаются неподвижными, наз. вращением тела вокруг неподвижной оси. тела из некоторого нач. положения.
тела из некоторого нач. положения. , кот. численной равен 1-й произв. от угла поворота
, кот. численной равен 1-й произв. от угла поворота 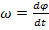 , а
, а  , где
, где  – вектор элементарного поворота тела за время
– вектор элементарного поворота тела за время 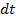 и направленный вдоль оси вращения так же как
и направленный вдоль оси вращения так же как  Произвольная т.М тв. тела, вращающегося вокруг неподвижной оси OZ с углов. ск-тью
Произвольная т.М тв. тела, вращающегося вокруг неподвижной оси OZ с углов. ск-тью  описывает окружность радиуса R центром в т.OI. Линейная ск-ть V м.т. М, направленная по касательной, и наз. лин ск-тью. Эта ск-ть направлена
описывает окружность радиуса R центром в т.OI. Линейная ск-ть V м.т. М, направленная по касательной, и наз. лин ск-тью. Эта ск-ть направлена  как к оси вращения Oz, т.е. к
как к оси вращения Oz, т.е. к  , проведенному из т.О и = векторному произведению.
, проведенному из т.О и = векторному произведению.  по модулю эта ск-ть =
по модулю эта ск-ть =  ) =
) =  .
. углового ускорения тела, равный 1-й произв. от его угл. ск-ти
углового ускорения тела, равный 1-й произв. от его угл. ск-ти 
 направл. вдоль оси вращения:
направл. вдоль оси вращения: , где
, где  – проекция угл. ск-ти на ось Oz.
– проекция угл. ск-ти на ось Oz. полностью определена, если заданы ее модуль, направление в пр-ве и точка приложения.
полностью определена, если заданы ее модуль, направление в пр-ве и точка приложения. , наз. стационарным полем, если оно не изменяется с теч. времени t
, наз. стационарным полем, если оно не изменяется с теч. времени t 
 ,
,  …
…  эквивалентно действию одной силы, называемой равнодействующей, или результирующей силой, и равной вект. сумме всех действующих сил
эквивалентно действию одной силы, называемой равнодействующей, или результирующей силой, и равной вект. сумме всех действующих сил 
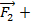 …+
…+  =
= 

 = произв. масс
= произв. масс  на
на  наз-ся импульсом или кол-ом движения этой мат.т.
наз-ся импульсом или кол-ом движения этой мат.т. , сумме сил, действ. на данную мат.т.
, сумме сил, действ. на данную мат.т.
 или исп. ур-е импульса:
или исп. ур-е импульса:  , т.к. m=const:
, т.к. m=const:  ;
; .
.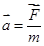
 ;
; ;
;
 ,
,  ,
,  .
.

 ,т.е. век-р всех внешних сил, равный геомтр. сумме всех внешн.сил
,т.е. век-р всех внешних сил, равный геомтр. сумме всех внешн.сил
 эта формула выражает з-н изменения импульса сист.
эта формула выражает з-н изменения импульса сист.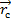 , кот.
, кот.  , где
, где 
 масса и радиус-вектор i-той м.т. N-общее число м.т-ек в сист.,
масса и радиус-вектор i-той м.т. N-общее число м.т-ек в сист.,  – масса всей системы.
– масса всей системы. ;
;  .
. (1). Где
(1). Где  - импульс системы.
- импульс системы.
 , где m – масса системы,
, где m – масса системы,  - ускорение центра масс.
- ускорение центра масс. точек тела и ск-ть центра масс
точек тела и ск-ть центра масс  одинаковы и равны
одинаковы и равны  тв. тела. Тогда ускорения тв. тела
тв. тела. Тогда ускорения тв. тела  = уск. сист. м.т.
= уск. сист. м.т.  (
( ) и основное ур-ние динамики поступат. движ. тв. тела имеет вид
) и основное ур-ние динамики поступат. движ. тв. тела имеет вид  .
. силу, с кот. k-я м.т. действует на i-ю.
силу, с кот. k-я м.т. действует на i-ю.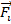 обозначим результирующую всех внешних сил, действующих на i-ю частицу. Тогда динамическое ур-ние движ. запишется в виде
обозначим результирующую всех внешних сил, действующих на i-ю частицу. Тогда динамическое ур-ние движ. запишется в виде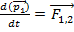 +
+  …+
…+  +
+  +
+  …+
…+  +
+ 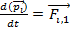 +
+  …+
…+  – импульс i-й частицы,
– импульс i-й частицы, 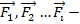 внешние силы, действующие на м.т.
внешние силы, действующие на м.т.
 .
. (1).
(1). , то в ур-нии (1) правая часть = 0.
, то в ур-нии (1) правая часть = 0. 
 и закон сохр. импульса сформулируется след. образом: суммарный импульс замкнутой сист. м.т. остается постоянным.
и закон сохр. импульса сформулируется след. образом: суммарный импульс замкнутой сист. м.т. остается постоянным. где
где  и
и 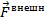 - главный вектор внешних сил, действующих на тело,
- главный вектор внешних сил, действующих на тело,  - ск-ть частиц после отделения от тела, если
- ск-ть частиц после отделения от тела, если  , или ск-ть присоединения, если
, или ск-ть присоединения, если 
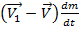 . Этот доп. член правой части ур-ния представляет собой доп. силу, действующую на тело переменной массы. Эта сила наз. реактивной силой
. Этот доп. член правой части ур-ния представляет собой доп. силу, действующую на тело переменной массы. Эта сила наз. реактивной силой  где
где 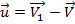 - ск-ть отделяющихся либо присоединяющихся частиц, т.е. их ск-ть по отношению к сист. отсчета, движущаяся поступательно вместе с телом, напр. ракетой.
- ск-ть отделяющихся либо присоединяющихся частиц, т.е. их ск-ть по отношению к сист. отсчета, движущаяся поступательно вместе с телом, напр. ракетой.
 струи газа. В этом случае
струи газа. В этом случае  и при
и при 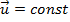 связь между ск-тью ракеты и ее массой по модулю выражается формулой Циалковского
связь между ск-тью ракеты и ее массой по модулю выражается формулой Циалковского  , где
, где  – начальная, стартовая масса ракеты с топливом и окислителем.
– начальная, стартовая масса ракеты с топливом и окислителем. где
где 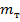 - начальная масса топлива и окислителя.
- начальная масса топлива и окислителя. где n – общее число ступеней ракеты;
где n – общее число ступеней ракеты;  - масса топлива и окислителя, предназначенных для работы i-той ступени;
- масса топлива и окислителя, предназначенных для работы i-той ступени; 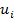 - cr-nm истечения газов i-той ступени;
- cr-nm истечения газов i-той ступени;  Моментом силы
Моментом силы  , равная вект. произведению
, равная вект. произведению 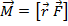 .
. производить вращение по наименьшему углу в направлении силы
производить вращение по наименьшему углу в направлении силы  ), α=
), α=  где α – наим. угол между векторами
где α – наим. угол между векторами  – длина перпендикуляра ОВ, опущенного из т.О на линию действия силы, где
– длина перпендикуляра ОВ, опущенного из т.О на линию действия силы, где 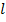 – наз-ся плечом силы относительно т.О. когда
– наз-ся плечом силы относительно т.О. когда  хар-ет способность силы вращать тело вокруг т.О, относит. кот. берется этот момент силы.
хар-ет способность силы вращать тело вокруг т.О, относит. кот. берется этот момент силы.
 , равный вект. произвед.
, равный вект. произвед.  проведенного из полюса О в место нахождения м.т., на вектор
проведенного из полюса О в место нахождения м.т., на вектор  импульса этой точки.
импульса этой точки.  , где
, где  - масса и ск-ть м.т.
- масса и ск-ть м.т. , где
, где  - масса, радиус-вектор и ск-ть i-той м.т., n – общее число этих точек в системе.
- масса, радиус-вектор и ск-ть i-той м.т., n – общее число этих точек в системе. . Если частица движется прямолинейно, то момент импульса может изменяться только за счет изменения модуля вектора ск-ти.
. Если частица движется прямолинейно, то момент импульса может изменяться только за счет изменения модуля вектора ск-ти.


