
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазовая скорость упругих волн в твердой средеСодержание книги
Поиск на нашем сайте Рассм. цилиндрич. стержень из однородного и изотропного материала
Предположим, что вдоль стержня распространяется плоская гармонич. волна. Частицы, лежащие в сечении стержня определяем координатой х, будут претерпевать смешение S, описываемое ур-нием Выделим в стержне элемент длины ∆x, ограниченной в отсутствие волны значением координаты x и x+∆x. Если сечение стержня в некоторый момент времени имеет смещение S, т.е. в момент возникновения волны, то смещение с координатой x+∆x будет S+∆S. Т.к. смещение сечений для разных значений координаты x описывается формулой (1), то они не одинаковы для разных x и этот элемент стержня будет деформирован. Он получает удлинение ∆S ≠∆x. Отношение Чтобы получить деформацию S в сечении с координатой x нужно устремить Относит. удлинение Деформация растяжения приводит к появлению в сечении с координатой x нормального упругого напряжения, описываемого формулой. Появление деформации в стержне приводит к появлению силы, проекция кот. на ось X равна Если подставить это выр. в ур-ние (2), то выр. для проекции силы перепишется в виде Учитывая, что масса = Ур-ние для плоской синусоид волны, распространяющейся вдоль оси X: Сравнив ур-ния (3) и (4) получим выражение для фазовой ск-ти продольных упругих волн стержня: Для поперечных волн:
Энергия упругой волны Упругая среда, в кот. распространяются мех. волны, обладает как кинет. энергией колебат. движения частиц, так и потенц. энергией, обусловленной деформацией. Для нахождения потенц. энергии упруго деформированного тела необходимо вычислить работу, кот. необходимо совершить, чтобы сообщить стержню длины Упругая силы, вызывающая это удлинение, = Значит в деформированной состоянии стержень обладает потенц. энергией Если в твердой среде с плотностью Выделим в стержне объем ДУ 2 один раз по t: Второй раз по x: Даст формулу плотности полной энергии, возникающей в упругой среде при распространении в ней плоской продольной гармонической волны
Кол-во энергии, переносимой волной за время Как энергия, так и поток энергии явл. величинами скалярными, в то же время мы говорим о направленном переносе энергии, тогда для хар-ки направления течения энергии в пр-ве используется вект. величина, наз. плотностью потока энергии
36.Принцин относительности Галилея или преобразования Галилея Рассм. движение частицы в 2-х инерциальных сист. отсчета – K и K', где сист. отсчета K' движется относит. сист отсчета K с пост. ск-тью. Для упрощение задачи пусть оси сист. коорд. x,y,z в сист. отсчета K ||-ны x',y',z' в сист. коорд. K' и пусть подвижная сист. отсчета K' движется вдоль оси X. В Ньютоновской мех-ке предполагается, что время во всех сист. отсчета течет одинаково, тогда исходя из наших упрощений, мы имеем 4 ур-ния, кот. связывают эти 2 инерц. сист. отсчета и эти ур-ния наз-ся преобразованиями Галилея.
Эти преобразования позволяют перейти от координат и времени одной инерц. сист. отсчета к координатам и времени другой инерц. сист. отсчета. Продиф-ем 1-е ур-ние по времени, учитывая, что Сумму всех этих ур-ний можно представить одним вект. урнием Дифференцирование ур-ния ск-ти по t и
37.Специальная теория относительности. Преобразования Лоренца Одни из основных постулатов мех-ки Ньютона явл. утверждение об одинаковости хода времени во всех инерц. СО и, как следствие этого, об абсолютности промежутков времени между какими-либо двумя событиями. Напр., если 2 события происходят одновременно по часам в одной инерц. СО, то они согласно классич. представлениям совершаются также одновременно по часам в любой другой инерц. СО. Это противоречит постулатам специальной теории относительности, которые применимы к эффектам, проявляющимся при скоростях движения тел близких к скорости света в вакууме, и эти ск-ти наз. релятивистскими ск-тями, а теория, описывающая такие явления, наз. релятивистской теорией.
Пусть имеются 2 ИСО – неподвижная K и система K', движущаяся вдоль оси X с пост. ск-тью В CO K' можно считать, что световая вспышка произошла в момент времени Согласно преобразованиям Галилея, Это противоречит классич. представлениями. В этом случае мы должны использовать не преобразования Галилея, а преобразования Лоренца. Преобразования Лоренца имеют простейший вид в том случае, если оси декартовых сист. коор. неподвижной K и движущейся K' ИС попарно параллельны и СО K' движется вдоль оси Х. Если дополнительно к этим условиям в качестве начала отсчета времени в обеих системах
Эти формулы дают возможность осущ. переход от сист. K к K' или от K' к K. Формулы для преобразований времени входят координаты. В пределе, когда С->∞, преобразования Лоренца переходят в преобразования Галилея.
Изменение длины тела Пусть стержень, длиной Отсюда
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |


 (1).
(1).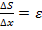 – среднее значение относительного удлинения элемента стержня ∆x.
– среднее значение относительного удлинения элемента стержня ∆x.
 =
=  , где
, где  - частная производная S по x, т.к. в общем случае S зависит от x и t.
- частная производная S по x, т.к. в общем случае S зависит от x и t. , E – модуль Юнга.
, E – модуль Юнга. , где
, где  - площадь поперечного сечения стержня. Т.к.
- площадь поперечного сечения стержня. Т.к.  мало, то мы можем воспользоваться св-вом производных для бесконечно малых величин:
мало, то мы можем воспользоваться св-вом производных для бесконечно малых величин:  .
. Для этого случая мы можем записать динамич. ур-ние движения 2-го зак. Ньютона.
Для этого случая мы можем записать динамич. ур-ние движения 2-го зак. Ньютона. и подставив это значение, мы можем записать равенство
и подставив это значение, мы можем записать равенство  . Сделав сокращение, получим волновое ур-ние
. Сделав сокращение, получим волновое ур-ние  . (3).
. (3). (4).
(4).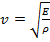 .
. , где G – модуль сдвига.
, где G – модуль сдвига. удлинение
удлинение 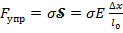 , где
, где  - модуль Юнга;
- модуль Юнга;  – нормальное напряжение в стержне, т.е. сила упругости, приходящаяся на единицу поперечного сечения;
– нормальное напряжение в стержне, т.е. сила упругости, приходящаяся на единицу поперечного сечения;  , где
, где  – относительное удлинение стержня длиной
– относительное удлинение стержня длиной 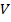 - объем стержня.
- объем стержня. , а плотность потенц эн.
, а плотность потенц эн.  .
.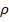 распространяется плоская продольная гармоническая волна, то скорость такой волны запишется как
распространяется плоская продольная гармоническая волна, то скорость такой волны запишется как  (2).
(2). , малый настолько, что скорость движения всех его частиц и относительную деформацию в каждом его сечении можно считать одинаковой. Поскольку скорость колебательного движения частиц среды равна производной
, малый настолько, что скорость движения всех его частиц и относительную деформацию в каждом его сечении можно считать одинаковой. Поскольку скорость колебательного движения частиц среды равна производной  , выделенный объем массой
, выделенный объем массой  обладает кинетической энергией
обладает кинетической энергией  . С другой стороны для потенц. эн. упругой деформации мы имеем
. С другой стороны для потенц. эн. упругой деформации мы имеем  . Мы используем в этих переходах значения для … и для
. Мы используем в этих переходах значения для … и для  , тогда полная энергия
, тогда полная энергия  , а плотность энергии
, а плотность энергии  .
. ;
;
 .
. , наз. потоком энергии
, наз. потоком энергии 
 (3), где
(3), где  - вектор фазовой ск-ти волны. Выр. 3 наз. вектором Умова-Пойнтинга.
- вектор фазовой ск-ти волны. Выр. 3 наз. вектором Умова-Пойнтинга. ;
;  .
. , т.е. производная по
, т.е. производная по 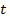 совпадает с производной по
совпадает с производной по  , тогда
, тогда  , где
, где  - проекция ск-ти частицы на ось X в сист. отсчета K;
- проекция ск-ти частицы на ось X в сист. отсчета K;  - проекц. ск-ти на ось
- проекц. ск-ти на ось 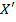 в сист. отсчета K', тогда
в сист. отсчета K', тогда 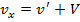 ;
; 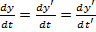 ;
;  .
. , т.е. ск-ть частицы относитю неподвижн. сист. отсчета K равна сумме скоростей частицы относит. подвижной СО и ск-ти системы K' относит. СО K.
, т.е. ск-ть частицы относитю неподвижн. сист. отсчета K равна сумме скоростей частицы относит. подвижной СО и ск-ти системы K' относит. СО K. даст
даст  , т.к. по условию
, т.к. по условию 

 . Пусть в нач. мом. времени
. Пусть в нач. мом. времени  начало коорд. K и K' совпадают. В мом. времени t=0 в т.О происходит вспышка света и одновременно с ней система K' начинает двигаться относительно системы K. В момент времени t>0 свет, распростр. со ск-тью с, достигает в CO K точек по-ти сферы с центром в т.О и радиусом ct.
начало коорд. K и K' совпадают. В мом. времени t=0 в т.О происходит вспышка света и одновременно с ней система K' начинает двигаться относительно системы K. В момент времени t>0 свет, распростр. со ск-тью с, достигает в CO K точек по-ти сферы с центром в т.О и радиусом ct. в т.О'.
в т.О'. выбран момент, когда нач. коорд. О и О' обеих систем совпадают, то преобразования Лоренца имеют наиболее простой вид:
выбран момент, когда нач. коорд. О и О' обеих систем совпадают, то преобразования Лоренца имеют наиболее простой вид:

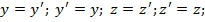
 ;
;  , где С- ск-ть света в вакууме; V – ск-ть подвижной СО K' относит. неподвижной K.
, где С- ск-ть света в вакууме; V – ск-ть подвижной СО K' относит. неподвижной K. , т.е. пр-во и время связаны между собой.
, т.е. пр-во и время связаны между собой. Если СО K' движется относит. K, то координаты стержня в СО K' по отношению K будут определяться формулами Лоренца:
Если СО K' движется относит. K, то координаты стержня в СО K' по отношению K будут определяться формулами Лоренца:  ;
;  ;
; 
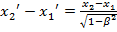 или в длинах стержня
или в длинах стержня  , т.е. длина стержня в движущейся CO K' будет меньше длины его в состоянии покоя на величину
, т.е. длина стержня в движущейся CO K' будет меньше длины его в состоянии покоя на величину  . Это явление наз. Лоренцевым сокращением.
. Это явление наз. Лоренцевым сокращением.


