Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложное движение материальной точкиСодержание книги
Поиск на нашем сайте
1. Движение МТ можно описать в разных СО. Выбор определяется удобствами. Движение МТ относительно подвижной СО – относительным движением Движение МТ относительно неподвижной СО, когда МТ покоится в подвижной СО – переносным движением. 2. Скорость МТ xоyz – подвижная СО вращается и движется поступательно 3. Закон сложения скоростей (теорема).
Примем - выражение для относительной скорости
закон сложения скоростей: 6. Ускорение (закон сложения ускорения).
Относительное ускорение в случае
При
Оставшееся выражение в формуле получило название ускорение Кориолиса.
Остаётся расшифровать переносное ускорение – на практике наиболее сложное.
Итог:
Аналогичным образом преобразуем выражение для кариолисового ускорения. В итоге получаем Динамика материальной точки. Основные понятия и законы 1. В науке недостаточно внешнего писания явлений, она вскрывает причины. Единственной причиной механического движения -механич.взаимодействие макроскопических тел на расстоянии и соприкосновении. По природе это гравитационные и электромагнитные взаимодействия. Принцип независимости взаимодействий: материальные причины взаимосвязи не могут зависеть от логики, цели, исчезать и появляться по желанию. 2. Основными понятиями являются: а) Ускорение материальной точки, сила, как характеристика действия, масса, как характеристика инертности. В механике 2 взаимодействия тел: появление ускорений; деформация тел С учетом явления и цели изучения строят модели тела, гениальная – материальная точка. 3. Законы динамики (Ньютона) 1. изолированная МТ находится в покое или равномерном прямолинейном движении (СО в которых это так называют ИСО) 2. ускорение МТ совпадает по направлению с направлением силы, прямо-пропорционально ей, обратно-пропорционально массе. 3. силы, с которыми действуют друг на друга 2 взаимодействующие МТ равны по величине, противоположны по направлениям. 4. Принцип суперпозиции сил:
если на МТ действует n сил, то каждая сила приводит к ускорению а1,..аn, которые в конечном итоге приводят к движению тела с ускорением а, это движение приводимой силы F. 3. Для описания мех.движения вводится система отсчета, наиболее простая – ИСО. В ИСО причиной ускоренного движения явл-ся материальное действие, т.е. реализуется механический детерменизм. Механическая эквивалентность ИСО фиксируется в принципе относительности Галилея:
По принципу независимости действий сила – инвариант, на основе 2 з-на Ньютона масса – инвариант. Дифференциальные уравнения движения. 1. Основное уравнение динамики МТ имеет вид.
Есть действие, есть сила. 2. Первая задача динамики состоит в нахождении законы силы по известным: x=x(t); y=y(t); z=z(t). Тогда простым умножением и дифференцированием можно найти вид функции силы, т.е.
3. Вторая задача динамики состоит в определении x=x(t); y=y(t); z=z(t) по известному закону сил. Решение второй задачи механики Вторая задача динамики состоит в определении x=x(t); y=y(t); z=z(t) по известному закону сил.
4. В общем, виде при решении системы ДУ (их три второго порядка, в итоге порядок системы шесть), получаем общее решение в виде функции:
Для получения частного решения необходимо определить постоянные Роль начальных условий. 1. Получается, что силы однозначно не определяют движение материальной точки. Однозначность решения определяется дополнительными условиями, которые называются начальными, это координаты и скорость в начальный момент времени при t=0.
2. Из этой системы выражающей начальные условия можно получить значения наших неопределённых постоянных.
Имеем право сейчас эти постоянные подставить в общее решение и получить уже частное решение в виде:
Эти кинематические уравнения описывают тот случай движения, который у нас действительно происходит. Принцип причинности. Если заданы силы и начальные условия, то в механике с помощью основного Ур-я можно предсказать состояние системы в любой момент прошлого и будущего. Эта идея получила название механический детерминизм. 1) возникает проблема с точностью определения начальных условий 2) в этой модели невозможно учесть действие случайных сил 3) модель не работает для большого числа частиц и в микромире. Это ограничивает строгий детерминизм.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.008 с.) |



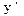 - неподвижная система отсчёта.
- неподвижная система отсчёта.

 ,
,  Если подвижная СО не движется, то r0=const, i, j, k=const
Если подвижная СО не движется, то r0=const, i, j, k=const Если МТ покоится в подвижной СО, а подвижная СО движется, то
Если МТ покоится в подвижной СО, а подвижная СО движется, то ,
,
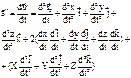
 (по определению).
(по определению).
 получаем выражение для переносного ускорения
получаем выражение для переносного ускорения



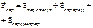
 ,
, 
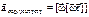 ,
, 
 , где
, где  - скорость движения материальной точки в подвижной системе отсчёта.
- скорость движения материальной точки в подвижной системе отсчёта.




 , где
, где  - результирующая.
- результирующая.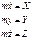 - проекции силы.
- проекции силы. , т.е. она состоит в решении системы дифференциальных уравнений. ДУ в ДСК.
, т.е. она состоит в решении системы дифференциальных уравнений. ДУ в ДСК. , т.е. она состоит в решении системы дифференциальных уравнений. ДУ в ДСК.
, т.е. она состоит в решении системы дифференциальных уравнений. ДУ в ДСК.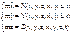 В полярной СК
В полярной СК  При естественном способе задания:
При естественном способе задания:

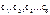 . Это же решение даёт семейство движений с одинаковым ускорением.
. Это же решение даёт семейство движений с одинаковым ускорением. Итак, получаем: t=0;
Итак, получаем: t=0;