
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения полной механической энергии.Содержание книги
Поиск на нашем сайте
1.Для произвольной системы МТ м-но записать теорему об изменении кинетической энергии в след-м виде:
2. Суммируем по всем точкам. 3. Дальнейшая конкретизация теоремы происходит при выборе ограниченных условий: а) если сист инерциальная, то б) если связи идеальные в итоге получаем для этих случаев теорему: в) дальнейшая конкретизация связана с уточнением вида сил. Если силы потенциальны и стационарны, т.е.
Условие потенциальности и стац-сти сил- сильный ограничитель, т.е. для большинства случаев при наличии сил з-на нет. г) при отсутствии сил (для идеального газа в МКТ) сохранение кинетической энергии системы Е(полн)=Т. д) вообще говоря в частных случаях и “Появление ” выполнения з-на сохр-я энергиизависит от видов сил, а их выбор в конкретных случаях за нами. З-ны сохранения связаны со свойствами пространства- времени.. Виртуальные перемещения. Обобщенные координаты. 1. АМ была разработана во второй половине 19 века, как вершина классической механики. В этой части механики разрабатывались наиболее обобщённые способы решения задач механики, она более абстрактна, но её методы получили развитие в электродинамике, квантовой механике. Это механика физической системы, но на другом языке. 2. Выберем систему n-материальных точек, между которыми действует m связей. Тогда в декартовой СК движение этих точек описывается системой 3n уравнений (для x, y, z) минус m-уравнений связей, то есть число независимых характеристик (уравнений) будет S=3n-m. Это число параметров уравнений, характеризующих движение системы называют числом степеней свободы системы. 3. Можно выбрать произвольно эти S-параметров, например q1, q2, q3,..., qs, которые будут полностью описывать движение системы (q1=q1(t) и т.д. – своеобразные уравнения движения). Очевидно, что между декартовыми координатами и этими параметрами существует однозначная взаимосвязь.
q – некий пар-тр, х-ка, обобщ-я координата. Ее смысл м.б. не коор-та, не метрич-я вел-на, а любая физ-я величина(импульс, момент им-са, момент инерции) м.б. обобщенной координатой. Простр-во, к-е задается S обобщенными коор-ми – конфигур-м пространством(n-мерное пр-во n измерений). В этом пр-ве полож-е системы зад-ся положением МТ. Действительные и виртуальные перемещения. 1. Понятие виртуального перемещения фундамент для аналитической механики; через него закладывается метод этой части. 2. Действительным перемещением Виртуальным перемещением называют мысленное бесконечно малое перемещение МТ, удовлетворяющее связям. В реальности таких перемещ-й нет. Скорее это метод ср-я движений по какому либо пар-ру. Виртуальное перемещение
dx-основнфя часть пр-ия ф-ии за dt. 1. Если задана функция
Принцип стационарного действия - принцип Гамильтона. 1. опис-е сис-мы состоит в отыскании ее кинематичи динамич.хар-к(x,y,z,…,m,p,E) при нал-ии тех или иных взаимодействий. Сущ-ет принцип к-й позвол. пол-ть ур-е движения в самом общем виде при извест.взаим-ях. 2. Содержание принципа: а) имеется сист-ма с известными взаим-ми. б) Можно построить функцию, которая хар-ет движение и взаим-е этой системы и значения в к-й момент времени t1 и t2. в) тогда сис-ма будет двиг-ся так, что:
3. принцип Гамильтона самый общий в физике; при неких хитростях построения L с помощью принципа м. получить Ур-е Ньютона, Максвелла, Шредингера.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.005 с.) |


 , теорема об изменении кинетической энергии системы МТ в общем случае.
, теорема об изменении кинетической энергии системы МТ в общем случае.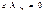 ,
,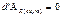 ,
, 
 ,.
,. ,
, 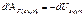 , то тогда получаем з-н сохранения полной механической энергии системы:
, то тогда получаем з-н сохранения полной механической энергии системы: 
 ,
, .
. м.б. потенциальной и стационарной (система НИСО- дв-е прямолинейное, равноускоренное), то в этом случае полная мех-я энергия сохраняется.
м.б. потенциальной и стационарной (система НИСО- дв-е прямолинейное, равноускоренное), то в этом случае полная мех-я энергия сохраняется.
 называют перемещение м. точек за время dt согласно Ур-ям движения МТ и уравнениям связи.
называют перемещение м. точек за время dt согласно Ур-ям движения МТ и уравнениям связи.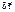 -вир-е переем-е.
-вир-е переем-е. представляют через вариации координат
представляют через вариации координат  . Сравним для противопоставления dx и
. Сравним для противопоставления dx и 
 =x2-x1 в момент времени t1(это сравнение нашего дв-я с возмож.близким дв-ем: в рамках математики это срав-е ф-ий по какому-либо пар-ру).
=x2-x1 в момент времени t1(это сравнение нашего дв-я с возмож.близким дв-ем: в рамках математики это срав-е ф-ий по какому-либо пар-ру).
 , то вариация
, то вариация  будет равна(t=0; δt=0):
будет равна(t=0; δt=0):
 - имеет экстремум, где L=L(
- имеет экстремум, где L=L( ) или вариация S=0
) или вариация S=0  . Этот интеграл пол-л название действия. L – ф-ия Лагранжа. Из условия δS=0 получим диф-е уравнение движения.
. Этот интеграл пол-л название действия. L – ф-ия Лагранжа. Из условия δS=0 получим диф-е уравнение движения.


