
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы движения и их значения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Состояние механической системы с S – степенями свободы, характеризуется 2S – параметрами – это координаты и проекции скоростей. Числом степеней свободы S называется число независимых параметров определяющих состояние системы, для свободной материальной точки – это 2. Весьма важными характеристиками любой системы является инварианты – сохраняющиеся величины (inv). Оказывается для решения второй задачи динамики часто достаточно отыскать такие инвариантные величины, которые получили название интегралов движения. В, общем, виде они получаются: так Из кинематических уравнений:
Получается система интегралов движения. Очевидно, что независимых уравнений (интегралов) из шести остаётся пять. 3. Пример:
Преобразуем к виду
Такое выделение резко упрощает решение задач. Интегралов движения много, но только некоторые полезны (связанные со свойствами пространства и времени, обладающие свойством аддитивности: импульс, энергия, момент импульса). Понятие связи. 1. Разнообразных материальных связей (взаимодействий) м/у телами очень много. Одни действия на тело м. описать силами, другие – трудно, а в теории - невозможно Связи – объективные условия (действия), ограничивающие движение тела (на языке моделей МТ). 2. Классификация связей. а) Удерживающая б) Неудерживающая в) Стационарная связь г) Нестационарная д) Неголономная связь е) Голономная связь
Наложение связи уменьшает число степеней свободы материальной точки на единицу, так как само уравнение связи устанавливает некую взаимосвязь (x,y,z), оставляет независимыми только две координаты. Если на материальную точку накладывается две связи заданные в виде уравнений поверхностей
Различают идеальные и неидеальные связи по принципу – работа идеальных связей равна нулю. Связь накладывает ограничения и на скорость материальной точки.
эта формула показывает, что Заданные силы и силы реакции. 1. По своей природе связь – всегда материальное действие, т.е. в принципе, в простых случаях связь м. заменить действием и его описать силой. Эта процедура называется принципом освобождения от связей. Если принцип применим, то уравнение движения несвободной МТ имеет вид:
3. Для шероховатой неподвижной поверхности (часто так) 4. Свойства силы а) б) в) при отсутствии ДУ движения (не свободной материальной точки). 1. Их получают из основного уравнения:
2. В декартовой системе отсчёта:
При естественном способе задания задается система отсчета «естественный трехгранник»:
Основное уравнение относительного движения материальной точки в НИСО. Принцип относительности. 1. В кинематике материальной точки нет принципиального различия между инерциальными и неинерциальными системами отсчёта. Различие систем отсчёта выражается лишь в формальной сложности уравнений, что не принципиально. 1. В динамике различия между системами отсчёта может быть принципиальным, в частности не во всех системах отсчёта выполняется великий закон 3. Оказывается, существуют такие системы отсчёта, в которых Такие системы отсчёта называют инерциальными, они друг относительно друга двигаются прямолинейно и равномерно. Для них
Классический принцип относительности выражается в инвариантности законов Ньютона, относительно преобразований Галилея. Силы инерции. 1. В случае НИСО, появляются ускорения, к-е нельзя объяснить действием матер. тел – это св-во системы. Ускорения, обусловленные самой системой отсчета сводятся к апер и акар. Вот и получаем
2. Выражениям скобкам может быть приписан смысл силы, их стали называть силами инерции.
Для общего случая при наличии связи имеем уравнение
3. Для случая покоя материальной точки в такой системе отсчёта получаем
Основное уравнение МТ в НИСО
Получаем уравнение: 2. Если связей нет, то r=0 и уравнение будет:
2. Если система отсчёта равномерно вращается (наша Земля), а МТ без связи, но движется, то:
Угловое ускорение: Принцип эквивалентности. 1. Принцип эквивалентности яв-ся обобщением опыта изучения и описания движений тел в разных СО. Он утверждает, что mr =kmr Локальное гравитационное поле равнозначно существованию НИСО, специально выбранных. Если локально-гравитационное поле эквивалентно поступательно и ускоренно движущейся СО, то тогда Ур-е движения МТ с одной стороны – в ИСО в гравитационном поле, с другой стороны – в НИСО без гравитационного поля должны иметь одинаковый вид. а) В ИСО при наличии поля имеем:
б) В НИСО поля нет (СО движется прямолинейно, равноускоренно, то МТ в СО покоится, но на нее действуют силы)
Его легко м. подобрать, чтобы было: Вывод: подбором НИСО м. создать ситуацию (локальную), когда ур-е движения МТ будет равносильно Ур-ю движения МТ в ИСО в гравитационном поле.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.49.73 (0.008 с.) |

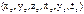 .
.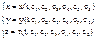 выражаем постоянные
выражаем постоянные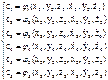
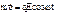
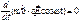
 - первый интеграл движения (сохраняется величина).
- первый интеграл движения (сохраняется величина). ;
;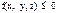 ;
;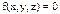 нет t (времени) – стационарная удерживающая связь;
нет t (времени) – стационарная удерживающая связь; ;
; - от скорости зависит;
- от скорости зависит;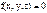 - от скорости зависит;
- от скорости зависит; - неудерживающая, нестационарная, неголономная связь.
- неудерживающая, нестационарная, неголономная связь.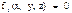 ,
, 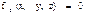 , то материальная точка имеет одну степень свободы, её движение осуществляется по кривой линии.
, то материальная точка имеет одну степень свободы, её движение осуществляется по кривой линии.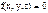

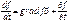
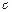 - вектор не может быть любым хотя бы по направлению.
- вектор не может быть любым хотя бы по направлению.
 - заданные силы;
- заданные силы; 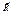 - реакция связей.
- реакция связей.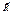 - реакция связей:
- реакция связей: 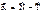 (где
(где 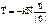 - закон Кулона).
- закон Кулона).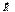 .
.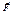 , у них есть свои св-ва.
, у них есть свои св-ва.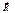 зависят от
зависят от 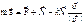 ; в зависимости от системы отсчёта получают разные системы уравнений; они сильно зависят от характера связи.
; в зависимости от системы отсчёта получают разные системы уравнений; они сильно зависят от характера связи. ,
, 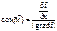
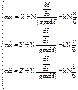
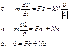 Решается сложно, т.к. не расшифровали Fτ, FN, Fb
Решается сложно, т.к. не расшифровали Fτ, FN, Fb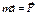 , не инвариантен при переходе из одной системы отсчёта в другую систему отсчёта, в частности мы доказали, что не инвариантно оказывается ускорение в разных системах отсчёта.
, не инвариантен при переходе из одной системы отсчёта в другую систему отсчёта, в частности мы доказали, что не инвариантно оказывается ускорение в разных системах отсчёта.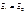 .
.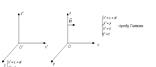 4. Переход из одной ИСО в другую управляется преобразованием Галилея, для простого случая:
4. Переход из одной ИСО в другую управляется преобразованием Галилея, для простого случая: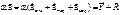 Þ по закону сложения ускорений при сложении движений материальной точки.
Þ по закону сложения ускорений при сложении движений материальной точки.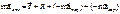
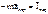 ,
, 
 - Основное уравнение динамики МТ в НИСО
- Основное уравнение динамики МТ в НИСО
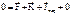

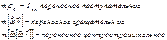
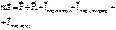
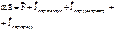
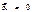
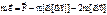 , при отсутствии связей свободное падение.
, при отсутствии связей свободное падение.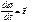
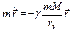 Гравитационная сила
Гравитационная сила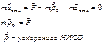
 =
= 



