
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Т. Об изменении импульса МТ.Содержание книги
Поиск на нашем сайте
Дв-е МТ м.б. описано на другом языке, нежели диф. ур-я движения. Это описание эквивалентно прежнему, но оно удобнее и проще. Теорема формируется из основного уравнения динамики.
Дифференциал количества движения или импульса, равен элементарному импульсу силы. В интегральном виде теорема имеет вид: В проекциях имеем:
Выводы: а) Теорема эквивалентна основному уравнению; б) Теорема даёт представление о материальном передатчике силы – передаче импульса от одного тела к другому; в) Теорема может быть использована в релятивистской области, таким образом, её содержание глубже второго закона Ньютона: З-н сохранения импульса. При определ условиях из теоремы получается закон. Это условие таково: Т. Об изменении момента импульса. 1. Определение момента силы. 2.
3. Определение момента импульса.
4.Т. об изменении момента импульса.
Докажем, что
Производная по времени от вектора момента импульса равна по величине и направлена по моменту силы. Теорема легко обобщается на случай разных сил, в т. ч. и сил инерции В проекциях получаем: З -н сохранения момента импульса. 1. Закон сохранения: если
В случае ИСО такое условие вып-ся легко- равенство 0 заданной силы и сил реакции связи. Важным является случай центральных сил- сила сонаправлена радиусу. 2. В НИСО в общ случае ЗСМИ не выполняется (т.к. всегда есть силы инерции). Но в нек-х случ проекция моментов сил на ось=0. отсюда сохранение одной из проекций момента импульса. 3. из 6 независимых интегралов дв-я всего 5 независимы. Док-во:
ЕСЛИ взять скалярное произв-е независимых только пять из шести векторов. Только для свободной материальной точки имеем шесть независимых интегралов движения. Только для свободной МТ два з-на созранения независимы. Работа силы. а) Определение. Для постоянной силы работа определяется Работа физическая величина, единица измерения [Дж], прямого измерения нет, характеризует действие на перемещении. б) Для элементарной работы существует определение:
Оказывается в общем случае правая часть, а значит и элементарная работа не является полным дифференциалом какой-либо функции. в) В интегральном виде для работы получаем
При преобразовании подынтегрального выражения пределы интегрирования может быть и по времени от Потенциальные силы. а) Определение. Потенциальной силой называют силу, которая удовлетворяет условию б) доказательство потенциальности силы может быть разное, в частности опирается на правило
в) Стационарное поле. Сила зависит от времени. СТАЦИОН-Я СИЛА-сила, к-я не зависит от времени.
элементарная работа для такой является дифференциалом функции При интегрировании получаем:
Видно, сто потенциальная энергия в точке зависит от выбора точки отсчёта, от выбора нулевой потенциальной энергии (нормировано), нет однозначности в определении U. Изменяемая лишь разность потенциальных энергий, т.е. работа. г) При определении потенциальности силы удобно использовать
если производная силы опред-ся так, то сила потенциальна. Нестационарная сила- большой класс сил, к-е зависят от времени.
В случае такой силы, у нас работу уже не выражается через разность потенциальной энергии; её расчёт более сложен.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.171 (0.008 с.) |

 ,
, 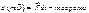 .
. 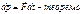 .
.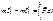
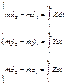
 =0(рез-я сила =0), т.е.
=0(рез-я сила =0), т.е. 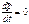 т.е.
т.е. 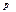 =const. =>
=const. =>  =const.
=const. 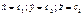 - первые интегралы движения. В общем случае (для любой СО и силы) имеем
- первые интегралы движения. В общем случае (для любой СО и силы) имеем  . Тогда з-н получается при условии
. Тогда з-н получается при условии 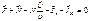 , это условие сложнее, реализуется реже, выполняется т-ко дщля проекции на 1 или 2 оси, т.е.
, это условие сложнее, реализуется реже, выполняется т-ко дщля проекции на 1 или 2 оси, т.е. 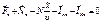 , тогда
, тогда 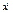 =с1- имеем з-н сохранения.
=с1- имеем з-н сохранения.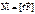 ,
, 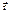 - радиус вектор, а значит, момент силы определяется относительно начала координат. Надо уметь определять проекции
- радиус вектор, а значит, момент силы определяется относительно начала координат. Надо уметь определять проекции 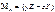 ;
; 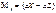
 .
. Определим момент силы относительно оси, как проекции этого вектора на эту ось (
Определим момент силы относительно оси, как проекции этого вектора на эту ось (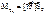 ), т.е. скал-я вел-на, при чем сам
), т.е. скал-я вел-на, при чем сам 
 . Учтём
. Учтём 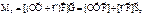
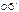 и
и 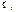 коллинеарные вектора Þ смешанное произведение равно нулю.
коллинеарные вектора Þ смешанное произведение равно нулю. 
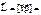 - момент импульса.
- момент импульса. 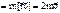 ,Проекции определяются
,Проекции определяются 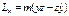 и т.д.
и т.д. - момент импульса. Для определения его ч-з кинематические Ур-я движения выполним проектирование.
- момент импульса. Для определения его ч-з кинематические Ур-я движения выполним проектирование. Проекции определяются
Проекции определяются  и т.д.
и т.д.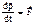 | - умножим слева векторно на r.
| - умножим слева векторно на r. 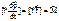
 ,
, 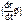 =0. Или получаем:
=0. Или получаем:  , или
, или 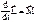
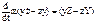 , и т.д.
, и т.д. , то
, то 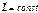 или
или - ещё три интеграла движения.
- ещё три интеграла движения.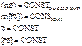
 =
=  т.е.
т.е. , скалярное произведение векторов.
, скалярное произведение векторов. , где
, где  - элементарный вектор перемещения.
- элементарный вектор перемещения.

 до
до  , так задачи решают, рассчитывая работу.
, так задачи решают, рассчитывая работу. (u-СКАЛЯРНАЯ ФУНКЦИЯ.)и которая не зависит от скорости и
(u-СКАЛЯРНАЯ ФУНКЦИЯ.)и которая не зависит от скорости и 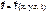
 , если
, если  .
.  , а, значит, проекции ротора на оси равны нулю, т.е.
, а, значит, проекции ротора на оси равны нулю, т.е. 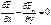 или
или  ;
;  и на другие оси подобные условия.
и на другие оси подобные условия. , тогда для работы имеем
, тогда для работы имеем
 .
. Т.е. работа не зависит от формы траектории, а определяется начальным и конечным положением.
Т.е. работа не зависит от формы траектории, а определяется начальным и конечным положением. , проинтегрируем:
, проинтегрируем:  ,
,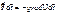


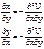
 Квазиупругая сила:
Квазиупругая сила:  .В общем случае имеем три подобных уравнения.
.В общем случае имеем три подобных уравнения.




