
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение адсорбции Гиббса и его естественно-научное и философское значение.Содержание книги
Поиск на нашем сайте
Рассмотрим вывод уравнения Гиббса, предложенный Ребиндером Если деформировать поверхность раздела фаз двухкомпонентной системы, то затраченная работа складывается из работы по созданию новой поверхности и работы по распределению компонентов между поверхностным слоем и объемами фаз:
Поверхность разрыва эквипотенциальна по растворителю (Г1 = 0), зн: Продифференцируем по μ:
Это уравнение характеризует равновесие м-ду объемными фазами и новым слоем при пост темп-ре. В состоянии равновесия между объемными фазами и поверхностным слоем:
Процессы адсорбции в коллоидных системах идут в сторону самопроизвольного увеличения градиента концентрации веществ на межфазной поверхности. Такие Для достаточно разбавленных растворов:
Уравнение Гиббса было проверено экспериментально на веществах, для которых Г › 0 и Г ‹ 0. Вещества, для которых Г › 0, снижают σ вещества, для которых Г ‹ 0, повышают σ, но незначительно – это ПИВ, поверхностно-инактивные вещества; вещества, которые не влияют на σ – поверхностно неактивные вещества (ПНВ). 2. Диффузионно-седиментационное равновесие и его использование для анализа Оседание частиц создает градиент концентрации частиц: их концетрация при приближении ко дну заметно увеличивается. Соответственно, возникает диффузионный поток Iдиф, направленный противоположно потоку седиментации Iсед, т. е. к верху пробирки.
Каков же результат конкуренции этих двух потоков? Возможны три варианта: Œ
Чтобы выполнилось это неравенство, значения Т и
Это условие должно выполнятся, когда Т и Ž
В системе имеет место диффузионно-седиментационное равновесие. Оно может наступить в золях через определенное, иногда очень длительное время. Так как такое равновесие наступает при определенном градиенте концентраций, в системе должно установиться соответствующее распределение частиц дисперсной фазы по высоте. После интегрирования и разделения переменных получим:
где М – молярная масса коллоидной частицы. В этом случае система является седиментационно-устойчивой, но распределение частиц в ней не равномерное, а равновесное. Это распределение наблюдается, когда 10-7 ‹ r ‹ 10-5 м, т. е. седиментационно-диффузионное равновесие устанавливается для микрогетерогенных систем. Историческое значение соответствующего уравнения заключается в том, что с его помощью впервые в истории науки было найдено значение важнейшей константы молекулярно-кинетической теории – число Авогадро. Он может быть получен как кинетич, так и термодинамическим путём.
Закон аналогичен барометрической формуле Лапласа для газов в атмосфере. Перрен в своих классических опытах с суспензией частиц гуммигута с известным радиусом r путем подсчета под микроскопом числа частиц на двух различных уровнях определил по этому уравнению значение NA = 6,7∙1023, весьма близкое к современному. Это соответствие найденного значения NA со значениями, полученными независимыми методами, показывает, что для коллоидных систем справедливы законы молекулярно-кинетической теории. 3. Что такое удельная поверхность адсорбента и как ее можно определить? удельная поверхность адсорбента -усреднённая характеристика размеров внутренних полостей (каналов, пор) адсорбента. Для расчёта удельная поверхность адсорбента используют Теория БЭТ: Согласно этой теории каждый адсорбционный центр sх связывает несколько молекул адсорбента Х, образуя цепочки: Уравнение, описывающее адсорбцию, выглядит следующим образом:
Для нахождения констант этого уравнения на основании экспериментальных данных строят график:
При При теория имеет практическое значение, т. к. можно определить удельную поверхность адсорбента. Величина а∞ зависит от энергетической равноценности поверхности и наличия пор. Для характеристики адсорбента используется понятие «пористость» П:
Какое отношение имеет минерал «драгоценный опал» к коллоидной химии? Для коллоидной химии опал- это дисперсии, обладающие анизотропными областями с хорошо выраженной периодичностью в расположении ориентированных относительно друг друга коллоидных частиц. Опал SiО2•nН2О – типичный твердый минеральный гель.Характерно проявление опалесценции — известный эффект Тиндаля: при прохождении светового пучка сквозь мутную среду со взвешенными частицами, размер которых составляет 0,1—0,2 длины волны падающего света, при взгляде сбоку на темном фоне появляется светлый (голубоватый) конус — так называемый "конус Тиндаля" 5. Изобразите формулы двух мицелл гидрозоля С, полученного из растворов веществ А и В в случае избытка вещества А или В. А - K3(Fe(CN)6), В - AgNO3, С - Ag3(Fe(CN)6) K3(Fe(CN)6)+ 3 AgNO3 = Ag3(Fe(CN)6) ↓ + 3 KNO3 1.Пусть в избытке K3(Fe(CN)6) {m[Ag3(Fe(CN)6)]n*Fe(CN)63-*3(n-x)K+}3x-*3xK+. 2. Пусть в избытке AgNO3 {m[Ag3(Fe(CN)6)]n*Ag+(n-x)* NO3-}x+*xNO3-. 6. Изобразите графически изменение ζ-потенциала для золя MnO2 (стабилизатор Na2S2O3) при добавлении к нему электролитов NaCl, AgNO3, KMnO4, Na2S2O3. Этот золь получают по уравнению: 8KMnO4 +3 Na2S2O3+ Н2О = MnO2↓+ К2SO4+КОН + 3 Na2SO4.

       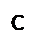
Если вносимые в систему электролиты являются индифферентными – не содержат таких ионов, которые были бы способны к специфической адсорбции на частицах по правилу Панета-Фаянса. Тогда повышение ионной силы оказывает двойное действие: уменьшение толщины диффузного слоя противоионов (d), сдвиг противоионов между плотным и диффузным слоями в сторону плотного слоя (уменьшение х – заряда частиц).
И то, и другое приводит к снижению -потенциала. Если это снижение достаточно сильное, дисперсные частицы начинают коагулировать. Коагуляция – важный процесс, и требует отдельного рассмотрения. Здесь же упомянем очевидное правило Шульце-Гарди: - коагулирующим действием обладают ионы, заряженные противоположно заряду частицы; - сила коагулирующего действия возрастает с увеличением заряда ионов; - при одинаковом заряде ионов коагулирующее действие возрастает с увеличением радиуса иона.
Билет 9. 1. Зависимость поверхностного натяжения от концентрации ПАВ. Уравнение Шишковского, физический смысл его констант и методы их определения.
Математическое описание зависимости σ( С ) дает уравнение Шишковского, полученное экспериментально при исследовании водных растворов жирных кислот: Приравняем выражения для ленгмюровской и гиббсовской адсорбций, что вполне справедливо для разбавленных растворов:
Разделим переменные и проинтегрируем:
Образование и строение двойного электрического слоя на границе раздела фаз. ДЭС – важнейший фактор, обеспечивающий агрегативную устойчивость дисперсных систем. В коллоидных системах он возникает в результате адсорбции ионов на поверхности частиц дисперсной фазы или диссоциации расположенных на поверхности функциональных групп и представляет собой систему пространственно разделенных зарядов противоположного знака на межфазной поверхности. В простейшем варианте его можно рассматривать как своеобразный конденсатор, обкладки которого состоят из противоположных по знаку зарядов, т. е. ДЭС – слой ионов одного знака + слой ионов второго знака (по теории Гельмгольца –Перрена). Различают адсорбцию ионов: избирательную и обменную. Избирательная адсорбция регулируется правилом Фаянса –Панета: На поверхности твердого тела, в том числе частицах дисперсной фазы, преимущественно адсорбируются те ионы, которые а) способны достраивать кристаллическую решетку твердого тела и об-разовывать с ионами, входящими в ее состав, нерастворимые соединения; б) присутствуют в растворе в избытке. Кроме того, могут адсорбироваться и изоморфные (близкие по структуре и размерам) с данной кристаллической Для объяснения строения ДЭС были предложены 3 теории: 1. График зависимости ψ(х) имеет вид:
Недостатки теории: –было установлено, что граница скольжения расположена от поверхности на большем расстоянии, чем молекулярные размеры; –согласно этой теории ζ = φ, но экспериментально установлено, что ζ < φ;
2. Теория Гуи – Чепмена. На твердой поверхности адсорбируются ионы определенного знака и, помимо электростатических сил, на их распределение влияет тепловое движение. Вследствие этого слой противоионов размыт. Распределение в нем зарядов подчиняется закону Больцмана: Достоинства теории: & ζ-потенциал рассматривается как часть φ-потенциала; & позволила понять действие индифферентных электролитов на ζ-потенциал.
–не учитываются размеры ионов, они рассматриваются как точечные заряды; –не объясняется явление перезарядки; –согласно этой теории различные ионы одинакового заряда должны одинаково сжимать ДЭС и снижать ζ-потенциал, но реально этого нет: чем больше радиус иона, тем сильнее он сжимает ДЭС и понижает ζ-потенциал. Работает только для разбавленных растворов. 3. Теория Штерна. Штерн объединил две предыдущие теории. Согласно его теории ионы – не точечные заряды, они имеют размеры и не могут находиться на расстоянии от поверхности меньшем, чем радиус иона. Помимо электростатического взаимодействия с твердой поверхностью существует специфическое адсорбционное. Эти силы действуют на небольших расстояниях, имеют адсорбционную природу и убывают с расстоянием быстрее, чем электростатические. Согласно этой теории существует два слоя противоионов: 1-й – адсорбционный слой (слой Гельмгольца, Штерна). Он удерживается на твердой поверхности электростатическими и адсорбционными силами; противоионы адсорбционного слоя равномерно распределены в слое, поэтому падение потенциала происходит линейно. 2-й – диффузный слой (слой Гуи). Это размытый за счет теплового движения слой оставшихся противоионов, который удерживается только электростатическими силами; его толщина – δ, он образуется теми противоионами, которые находятся на заряженной поверхности на расстоянии, большем, чем диаметр гидратированного противоиона d, но в пределах расстояния δ. Эти противоионы притягиваются к частице только за счет электростатических сил, а следовательно, менее прочно, чем противоионы адсорбционного слоя. При движении частицы двойной электрический слой разрывается. Место разрыва при перемещении твердой и жидкой фаз друг относительно друга называется плоскостью скольжения. На рисунке плоскость скольжения обозначается пунктирной линией. Плоскость скольжения лежит либо на границе между диффузным и адсорбционным слоями, либо в диффузном слое, но вблизи этой границы. Потенциал на плоскости скольжения называется электрокинетическим или ζ-потенциалом. Электрокинетический потенциал является важнейшей характеристикой ДЭС. Согласно этой теории при введении электролитов в систему ионы из диффузионного слоя переходят в адсорбционный слой из-за чего ζ-потенциал уменьшается и может достичь нуля. При разбавлении системы ζ-потенциал увеличивается. На размер ДЭС сильно влияет природа противоионов: • чем больше валентность противоиона, тем меньше ДЭС и меньше ζ-потенциал. Если валентность одинакова, то толщина диффузного слоя и ζ-потенциал определяются специфической адсорбцией – увеличение адсорбции вызывает сжатие слоя; • чем больше радиус иона (чем меньше гидратируемость), тем меньше ДЭС; • чем больше поляризуемость, тем меньше ДЭС.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.4 (0.014 с.) |

 .(Механическая работа и Химическая работа)
.(Механическая работа и Химическая работа) .
. . Запишем левую часть полученного уравнения в виде:
. Запишем левую часть полученного уравнения в виде: 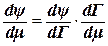 . Величина
. Величина 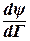 , как производная энергии по количеству вещества, соответствует химическому потенциалу и выражает изменение поверхностной энергии с увеличением адсорбции растворенного вещества.
, как производная энергии по количеству вещества, соответствует химическому потенциалу и выражает изменение поверхностной энергии с увеличением адсорбции растворенного вещества. ;
;  – термодинамическое уравнение адсорбции Гиббса.
– термодинамическое уравнение адсорбции Гиббса.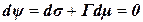 , т.е. можно несколько условно сказать, что минимуму свободной энергии системы на единицу площади поверхности (при заданной величине адсорбции Г) соответствует равновесие между «механическими» и «химическими» силами, т.е. между стремлением системы к уменьшению поверхностной энергии за счет концентрирования в поверхностном слое некоторых веществ и невыгодностью такого концентрирования из-за возрастания их химического потенциала.
, т.е. можно несколько условно сказать, что минимуму свободной энергии системы на единицу площади поверхности (при заданной величине адсорбции Г) соответствует равновесие между «механическими» и «химическими» силами, т.е. между стремлением системы к уменьшению поверхностной энергии за счет концентрирования в поверхностном слое некоторых веществ и невыгодностью такого концентрирования из-за возрастания их химического потенциала. системы в процессе диспергирования способны совершать полезную работу за счет градиента хим. потенциала.
системы в процессе диспергирования способны совершать полезную работу за счет градиента хим. потенциала.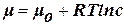 .
.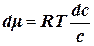 ;
;  – уравнение Гиббса для разбавленных растворов.
– уравнение Гиббса для разбавленных растворов. – это ПАВ, поверхностно-активные вещества;
– это ПАВ, поверхностно-активные вещества; дисперсных систем.
дисперсных систем. , где ν – концентрация частиц ДФ.
, где ν – концентрация частиц ДФ. , где h – высота.
, где h – высота. , т. е.
, т. е. 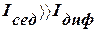 , т. е.
, т. е.
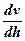 должны быть малы, а (ρ-ρо) и ν – велики. В реальных условиях эти параметры заметно изменить сложно, а радиус частиц в дисперсной системе изменяется в широком интервале: от 10-9 до 10-4 м и именно радиус частиц является определяющим. Установлено, что данное неравенство соблюдается, когда r ≥ 10-5 м. В этих случаях диффузией можно пренебречь, идет быстрая седиментация – система является седиментационно неустойчивой.
должны быть малы, а (ρ-ρо) и ν – велики. В реальных условиях эти параметры заметно изменить сложно, а радиус частиц в дисперсной системе изменяется в широком интервале: от 10-9 до 10-4 м и именно радиус частиц является определяющим. Установлено, что данное неравенство соблюдается, когда r ≥ 10-5 м. В этих случаях диффузией можно пренебречь, идет быстрая седиментация – система является седиментационно неустойчивой.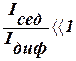 , т. е.
, т. е.  , т. е.
, т. е.
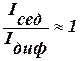 , т. е.
, т. е. 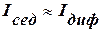 , т. е.
, т. е.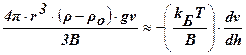
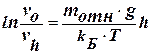 – гипсометрический закон распределения частиц (закон Лапласса-Перрена-Больцмана), характеризующий распределение частиц по высоте в условиях диффузионно-седиментационного равновесия и позволяющий определить молекулярные массы частиц:
– гипсометрический закон распределения частиц (закон Лапласса-Перрена-Больцмана), характеризующий распределение частиц по высоте в условиях диффузионно-седиментационного равновесия и позволяющий определить молекулярные массы частиц: ,
,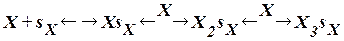 .
.
 , где
, где 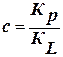 ; Кр – константа адсорбции; КL – константа конденсации.
; Кр – константа адсорбции; КL – константа конденсации. . Это уравнение работает только в интервале
. Это уравнение работает только в интервале 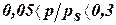 , в котором предполагается отсутствие взаимодействия между цепочками адсорбированных молекул.
, в котором предполагается отсутствие взаимодействия между цепочками адсорбированных молекул. – большая степень заполнения, возникают боковые взаимодействия между молекулами.
– большая степень заполнения, возникают боковые взаимодействия между молекулами. – малая степень заполнения, на величину адсорбции сильно влияют энергетические неоднородности поверхности.
– малая степень заполнения, на величину адсорбции сильно влияют энергетические неоднородности поверхности. , где sо – площадь, занимаемая молекулой адсорбата.
, где sо – площадь, занимаемая молекулой адсорбата.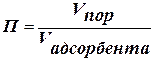 .
.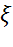
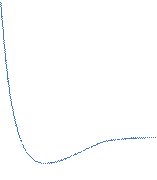
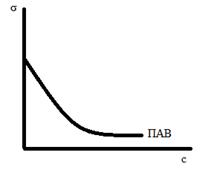 Поверхностно-активные вещества – вещества, которые при адсорбции на границе раздела понижают ее поверхностное натяжение. Такие вещества имеют тенденцию переходить из объема раствора на его поверхность, т. е. происходит их концентрирование на межфазной поверхности. Зависимость поверхностного натяжения раствора от концентрации растворенного вещества при постоянной температуре называется изотермой поверхностного натяжения. ПАВ обладают следующими свойствами: их поверхностное натяжение меньше поверхн. натяжения растворителя; они характеризуются малой растворимостью. При увеличении концентрации ПАВ в растворе его поверхностное натяжение уменьшается по экспоненциальному закону и выходит на плато (прямую) при некоторой концентрации, отвечающей полному заполнению поверхностного слоя молекулами ПАВ. На рисунке изотерма поверхностного натяжения.
Поверхностно-активные вещества – вещества, которые при адсорбции на границе раздела понижают ее поверхностное натяжение. Такие вещества имеют тенденцию переходить из объема раствора на его поверхность, т. е. происходит их концентрирование на межфазной поверхности. Зависимость поверхностного натяжения раствора от концентрации растворенного вещества при постоянной температуре называется изотермой поверхностного натяжения. ПАВ обладают следующими свойствами: их поверхностное натяжение меньше поверхн. натяжения растворителя; они характеризуются малой растворимостью. При увеличении концентрации ПАВ в растворе его поверхностное натяжение уменьшается по экспоненциальному закону и выходит на плато (прямую) при некоторой концентрации, отвечающей полному заполнению поверхностного слоя молекулами ПАВ. На рисунке изотерма поверхностного натяжения.

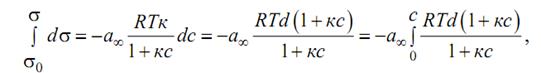
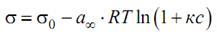 – это уравнение является теоретическим аналогом эмпирического уравнения Шишковского, которое было им получено при исследовании зависимости поверхностного натяжения водных растворов одноосновных карбоновых кислот от их концентрации:
– это уравнение является теоретическим аналогом эмпирического уравнения Шишковского, которое было им получено при исследовании зависимости поверхностного натяжения водных растворов одноосновных карбоновых кислот от их концентрации:
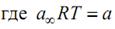 константа, одинаковая для всех членов одного гомологического ряда и мало изменяющаяся для различных рядов с неразветвленными цепями, в – константа адсорбционного равновесия, индивидуальная для каждого ПАВ. Согласно уравнению Шишковского, с ростом с ПАВ σ убывает по логарифмическому закону. При умеренных концентрациях это справедливо. Но для больших концентраций получаем неверный результат: при с→∞ σ стремится к отрицательным значениям, чего, конечно, не может быть. В этом – недостаток данного уравнения. Однако если перейти к поверхностной активности, указанный недостаток становится не столь заметным.С помощью уравнений Гиббса и Ленгмюра можно прояснить физический смысл констант a и b. Константа a связана с величиной максимальной адсорбции a = RT Гmax и не зависит от длины углеводородного радикала молекулы ПАВ только при условии вертикальной ориентации дифильных молекул и их плотной упаковки. Константа b из уравнения Шишковского совпадает с величиной поверхностной активности из уравнения Ленгмюра.
константа, одинаковая для всех членов одного гомологического ряда и мало изменяющаяся для различных рядов с неразветвленными цепями, в – константа адсорбционного равновесия, индивидуальная для каждого ПАВ. Согласно уравнению Шишковского, с ростом с ПАВ σ убывает по логарифмическому закону. При умеренных концентрациях это справедливо. Но для больших концентраций получаем неверный результат: при с→∞ σ стремится к отрицательным значениям, чего, конечно, не может быть. В этом – недостаток данного уравнения. Однако если перейти к поверхностной активности, указанный недостаток становится не столь заметным.С помощью уравнений Гиббса и Ленгмюра можно прояснить физический смысл констант a и b. Константа a связана с величиной максимальной адсорбции a = RT Гmax и не зависит от длины углеводородного радикала молекулы ПАВ только при условии вертикальной ориентации дифильных молекул и их плотной упаковки. Константа b из уравнения Шишковского совпадает с величиной поверхностной активности из уравнения Ленгмюра. структурой ионы. Способность к адсорбции зависит от заряда и размера иона: чем больше размер иона, тем меньше плотность заряда и меньше размеры гидратной оболочки, следовательно, тем легче адсорбируется ион. ДЭС образуется не только на поверхности частиц золей, но и эмульсий.
структурой ионы. Способность к адсорбции зависит от заряда и размера иона: чем больше размер иона, тем меньше плотность заряда и меньше размеры гидратной оболочки, следовательно, тем легче адсорбируется ион. ДЭС образуется не только на поверхности частиц золей, но и эмульсий. Теория Гельмгольца – Перрена. Они представляли ДЭС в виде плоского конденсатора, обкладки которого состоят из слоев противоположных зарядов и расположены на расстоянии порядка молекулярного диаметра. Падение потенциала между слоями ДЭС происходит линейно в зависимости от расстояния от поверхности раздела фаз.
Теория Гельмгольца – Перрена. Они представляли ДЭС в виде плоского конденсатора, обкладки которого состоят из слоев противоположных зарядов и расположены на расстоянии порядка молекулярного диаметра. Падение потенциала между слоями ДЭС происходит линейно в зависимости от расстояния от поверхности раздела фаз.
 –так как по этой теории ζ = φ, то они одинаково зависят от присутствия индифферентных электролитов. Однако было показано, что φ-потенциал не зависит от присутствия индифферентных электролитов, а ζ-потенциал зависит достаточно сильно.
–так как по этой теории ζ = φ, то они одинаково зависят от присутствия индифферентных электролитов. Однако было показано, что φ-потенциал не зависит от присутствия индифферентных электролитов, а ζ-потенциал зависит достаточно сильно. где Wi – работа против сил электростатического притяжения к поверхности. Т. е. имеем облако зарядов с экспоненциально убывающей плотностью. Из графика видно, что чем больше концентрация зарядов, тем круче кривая.
где Wi – работа против сил электростатического притяжения к поверхности. Т. е. имеем облако зарядов с экспоненциально убывающей плотностью. Из графика видно, что чем больше концентрация зарядов, тем круче кривая.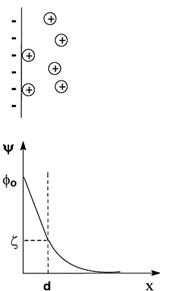 Недостатки теории:
Недостатки теории:


