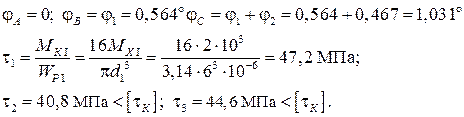Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетно - графических работСодержание книги Поиск на нашем сайте ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНО - ГРАФИЧЕСКИХ РАБОТ При изучении курса «Сопротивление материалов» студенты выполняют расчетно-графические работы, состоящие из контрольных задач по основным разделам изучаемого курса. Количество расчетно-графических работ и задач в них определяется учебными планами по соответствующим специальностям. Контрольные задачи имеют индивидуальный характер: расчетные схемы и числовые данные для каждой задачи выбираются по шифру, состоящему из шести цифр. В зависимости от задания используются все шесть цифр шифра или только несколько цифр шифра. Шифр определяется по первым буквам фамилии, имени, отчества студента в зависимости от кодов этих букв, приведенных в таблице.
Задания выполняются на листах бумаги формата А4 (210x297), а чертежи к ним (с обязательным соблюдением масштаба) на миллиметровой бумаге того же формата. Обложка работы оформляется по образцу, приведенному в приложении 4. Перед выполнением каждого задания выписываются условия с исходными данными и составляется в масштабе чертеж, на котором указываются численные значения заданных величин. Все этапы решения нумеруются в соответствие с пунктами, указанными в условии, и снабжаются кратким пояснением. При расчете вначале выписываются используемые формулы с применением общепринятых буквенных обозначений, затем подставляются исходные данные вместо буквенных обозначений в той же последовательности и после этого производятся требуемые математические вычисления. Все численные расчеты требуется проводить в системе СИ. Окончательные результаты с обязательным указанием размерности в Международной системе СИ выделяются (подчеркиваются или берутся в рамки). После выполнения расчетно-графические работы предъявляются преподавателю для защиты не позднее срока, предусмотренного учебным планом. Примечание: Студент должен выбрать тип задачи и размеры в соответствии со своим шифром. Для этого следует написать шифр, а под ним буквы алфавита в определенном порядке. Например:
В таблице буквы стоят в конце колонок с соответствующими данными к задаче. Цифры, стоящие выше букв, показывают, из какой строки следует выбрать нужный параметр. Методические указания предназначены в помощь студентам машиностроительных специальностей при их самостоятельной работе над типовыми расчетами. В данной работе изложены методические указания по выполнению расчетно-графических работ для студентов по разделам: сдвиг, напряженное и деформированное состояние в точке, кручение стержня с круглым поперечным сечением (определение внутренних усилий, расчеты на прочность и жесткость: определение напряжений, деформаций, перемещений,). геометрические характеристики плоских сечений. Приводятся примеры решения типовых задач, а также задания для выполнения контрольных и расчетно-графических работ.
СДВИГ НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ
Для исследования напряженного состояния в точке деформируемого тела в ее окрестности выделяют элементарный объем в виде прямоугольного параллелепипеда (рис. 2). В общем случае деформирования напряженное состояние в точке характеризуется девятью величинами: тремя нормальными напряжениями σ x, σ y и σ z и шестью касательными напряжениями – τ xy, τ xz, τ yz, τ zx, τ yx, τ zy. Вследствие закона парности касательных напряжений (τ yz = τ zy, τ zx = = τ xz, τ xy = τ yx) число независимых компонентов уменьшается до шести.
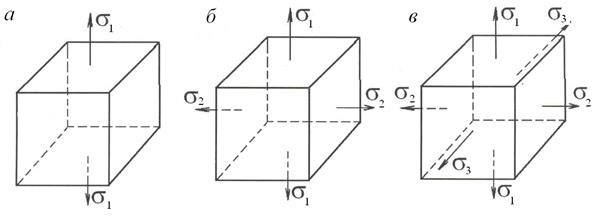
Рис. 2. Объемное напряженное состояние Исследование напряженного состояния включает определение напряжений по произвольной площадке, проходящей через данную точку, а также положение главных площадок и значений главных нормальных напряжений. Среди бесконечно большого числа площадок, проходящих через данную точку тела, всегда найдутся по крайней мере три взаимно перпендикулярные площадки, на которых касательные напряжения отсутствуют. Такие площадки носят название главных площадок, а нормальные напряжения на них – главных нормальных напряжений. Напряженное состояние в любой точке можно свести к растяжению или сжатию по одному, двум или трем взаимно перпендикулярным направлениям. В зависимости от этого различают линейное, плоское и объемное напряженное состояние (рис. 3).
Рис. 3. Виды напряженного состояния: а – линейное; б – плоское; в – объемное
Очень важно уметь определять значения главных нормальных напряжений в случае плоского напряженного состояния, которое наиболее часто встречается в брусе, подвергающемся действию изгибающих, скручивающих и растягивающих нагрузок, а также в тонкостенных оболочках.
Пример 1
Исследовать плоское напряженное состояние стального кубика (рис. 4, а).
Рис. 4. Hормальные и касательные напряжения по граням кубика: а – направления напряжений для исследуемого напряженного состояния; б – положительные направления напряжений Абсолютные величины напряжений (см. рис. 4, а): σ x = 100 МПа; σ y = 70 МПа; τ xy = τ yx = 50 МПа; Е = 2 ·105 МПа; μ = 0,25. Прежде всего установим знаки нормальных и касательных напряжений, показанных на рис. 4, а. Положительные направления нормальных напряжений σ x, σ y и касательных напряжений τ xy = τ yx показаны на рис. 4, б. Нормальные растягивающие напряжения принято брать со знаком плюс, а сжимающие – со знаком минус. Следовательно, σ x = –100 МПа и σ y = 70 МПа, τ xy = –50 МПа. Определение главных напряжений. Наибольшее σ1:
наименьшее из главных напряжений σ2 :
Определение направления главных площадок. Угол наклона нормали главной площадки к оси X определяется по формуле
Знак касательных напряжений и угла α можно неустанавливать, если пользоваться следующим правилом для определения ориентации главных площадок. Главные площадки, на которых действует наибольшее из главных напряжений σ1, получаются поворотом на угол α тех из исходных площадок, на которых действует большее (по алгебраической величине) из исходных напряжений σ x, σ y. В нашем примере такими исходными площадками будут площадки, где действует нормальное напряжение σ y, так как σ y > σ x. Направление поворота указывает стрелка касательного напряжения на исходной площадке (рис. 5). Вторая пара главных площадок перпендикулярна найденным. Определение максимальных касательных напряжений:
Эти напряжения действуют на площадках, наклоненных под углом 45° к главным, и направлены в сторону σ1 (см. рис. 5).
Рис. 5. Расположение главных площадок
Определение относительных деформаций ε x, ε y, ε z:
Обратите внимание на то, что при σ z = 0 ε z ≠ 0, т.е. при отсутствии напряжения по оси Z деформация в этом направлении имеет место.
Определение относительного изменения объема θ:
Определение удельной потенциальной энергии деформаций. Потен- циальная энергия изменения объема U об:
U об
Потенциальная энергия изменения формы U ф: U ф
Полная энергия U: U = U об + U ф = 46·10–3 = 46·10–3 МПа (Н/мм2).
Вопросы для самоконтроля 1. Что такое напряженное состояние в точке? 2. Дайте понятие главных напряжений и трех основных видов напряженного состояния. 3. Чему равны касательные напряжения в главных площадках? 4. Как устанавливаются величины главных напряжений и положение главных площадок для плоского напряженного состояния? 5. Как расположены площадки с напряжениями τmax и как они выражаются через главные напряжения? 6. Как связаны относительные линейные и объемная деформации в точке? 7. Напишите выражения удельной потенциальной энергии деформации в общем случае напряженного состояния в точке. 8. Что называется коэффициентом поперечной линейной деформации? 9. Как определяется линейная деформация при трехосной нагрузке? 10. Как формулируется закон парности касательных напряжений?
КРУЧЕНИЕ
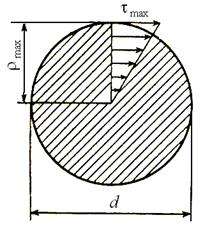
При кручении в поперечном сечении стержня возникает крутящий момент М К. Нагрузкой при кручении являются скручивающие моменты mi, действующие относительно продольной оси стержня. Крутящий момент определяется методом сечений и равен алгебраической сумме внешних (скручивающих) моментов, действующих на рассматриваемую часть стержня: М К = ∑ mi. Момент считается положительным, если он направлен против хода часовой стрелки (при взгляде со стороны сечения). При кручении в поперечном сечении стержня возникают касательные напряжения τ. Касательные напряжения τ распределяются по площади круглого поперечного сечения стержня неравномерно, нарастая от оси вала к поверхности по линейному закону, наибольшие напряжения возникают по контуру сечения. Закон распределения напряжений τ вдоль произвольного радиуса в сечении изображен на рис. 13. Во всех точках окружности радиуса ρ напряжение τ = const и направлено по касательной к этой окружности. Напряжения τ в сечении сводятся к крутящему моменту М К(рис.7): М К = Формула для определения τ имеет вид
где Ip – полярный момент инерции сечения, м4; для сплошного круглого сечения М К – крутящий момент, Н·м.
Рис. 7. Распределение касательных напряжений в сечении при кручении Условие прочности имеет следующий вид:
где [τк] – допускаемое напряжение на кручение, Па. Для сплошного круглого сечения (рис. 14)
Рис.8. К определению полярного момента сопротивления Wp длясплошного круглого сечения Для полого толстостенного цилиндра (рис. 9)
Рис. 9. К определению полярного момента сопротивления Wp дляполого толстостенного цилиндра Деформация при кручении характеризуется углом закручивания на единицу длины стержня θ:
Величина θ называется относительным углом закручивания и имеет размерность рад/м или град/м. Условие жесткости имеет вид
где G – модуль упругости материала при сдвиге, Па. Зависимость между модулями упругости Е и G имеет вид
где μ – коэффициент Пуассона; [θ] – допускаемый относительный угол закручивания на единицу длины стержня (рад/м). Диаметр стержня, работающего на кручение, определяется из двух условий: прочности и жесткости. Во внимание берется наибольший диаметр. Окончательное значение его принимается согласно стандарту.
Пример 2
Определить диаметры поперечных сечений участков стержня (вала) (рис. 16, а), если [τK] = 100 МПа, G = 80 ГПа, [θ] = 1,5о/м. Построить эпюру углов поворота сечений φ. [θ] = 1,5о/м =
Рис.10. Построение эпюр крутящих моментов М к углов поворота сечений φ: а – расчетная схема; б – эпюра крутящих моментов М к; в – эпюра углов поворота сечений φ
Должно выполняться условие равновесия ∑ mx = 0: ∑ mx = m 1 – m 2 – m 3 + m 4 = 2 – 1 – 4 + 3 = 0. Для определения крутящих моментов М к на участках стержня будем рассматривать левую часть его. Участок I: М KI = m 1 = 2 кН·м. Участок II: М KII = m 1 – m 2 = 2 – 1 = 1 кН·м. Значение М КIII определите самостоятельно (М КIII = – 3 кН·м). По вычисленным значениям М к строится эпюра (см. рис. 16, б). Преобразуем условия прочности и жесткости к виду, удобному для определения диаметра стержня. Условие прочности:
Условие жесткости:
откуда
Вычисляем диаметр вала из условий прочности и жесткости. На первом участке: – диаметр вала из условия прочности
– диаметр вала из условия жесткости
Принимаем d 1 = 6 см. На втором участке: – диаметр вала из условия прочности
– диаметр вала из условия жесткости
Принимаем d 2 = 5 см. Диаметр поперечного сечения на участке III рассчитайте самостоятельно (d 3 = 5,35 см, d’ 3 = 6,18 см, принимаем d 3 = 7 см). Если стержень имеет постоянное сечение, то диаметр его определяется исходя из максимального значения М к. Определим деформации участков стержня:
Значения φ на других участках следующие:
Углы поворота характерных сечений (границ участков) равны:
Значение φ D определите самостоятельно (φ D = – 0,429о). Эпюра углов поворота сечений показана на рис. 16, в. Вычислим максимальные напряжения на участках стержня:
Вычисленные значения диаметров участков стержня обеспечивают его прочность и жесткость.
Задача 2 Вопросы для самоконтроля
1. При какой нагрузке на брус получается деформация, называемая кручением? 2. Какая зависимость существует между модулями упругости G и Е? 3. Что называется крутящим моментом? 4. Как распределяются касательные напряжения по площади круглого сечения при кручении? 5. Как выражаются касательные напряжения при кручении через величину крутящего момента? 6. Как определяются относительный и абсолютный углы закручивания вала? 7. Какая существует дифференциально-интегральная зависимость между τ, М к, φ, θ? 8. В чем состоит расчет на прочность и жесткость валов? 9. Что такое момент сопротивления сечения при кручении? В чем состоит условие прочности? 10. Как найти диаметр сечения вала, удовлетворяющего условиям прочности и жесткости? 11. Как формулируется закон Гука при сдвиге?
Вопросы для самоконтроля
1. По каким формулам определяются координаты центра тяжести сечения? 2. Для каких сечений при определении центра тяжести достаточно найти только одну координату? 3. Что называется осевым, центробежным и полярным моментами инерции сечения? 4. Какова размерность моментов инерции? 5. Чему равен осевой момент инерции прямоугольника относительно центральной оси параллельной основанию? 6. Относительно, каких центральных осей осевые моменты инерции имеют наибольшее и наименьшее значения? 7. Запишите зависимость для осевого момента инерции при параллельном переносе осей. 8. Как определяется положение главных осей?
Литература Основная 1. Межецкий Г. Д. Сопротивление материалов: учебник / Г. Д. Межецкий, Г. Г., Загребин, Н. Н. Решетник; под общ. ред.. Г. Д. Межецкого, Г. Г. Загребина. - 3-е изд., перераб. и доп. - М.: Издательско-торговая корпорация «Дашков и К», 2011. – 432 с. 2. Кривошапко С.Н. Сопротивление материалов: учебник для вузов [Гриф Минобразования РФ] / С. Н. Кривошапко. - Москва: Юрайт, 2012. - 413 с.
Дополнительная 3. Александров А. В. Сопротивление материалов: учебник для вузов/ 4. Наседкина З.А. Сопротивление материалов [Текст]: учеб. пособие/ 5. Смирнов А. Ф. Сопротивление материалов: учебник / А. Ф. Смирнов, А. В. Александров, И.И. Монахов и др.; под общей ред. А. Ф. Смирнова. 6. Сборник задач по курсу «Сопротивление материалов» / Сост. 7. Задания и методические указания для выполнения контрольных расчетно-графических работ по дисциплине «Сопротивление материалов» (ГОС – 2000) / Сост. З.А. Наседкина, А.В. Песков. - Екатеринбург, ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2010. 32 с. 8. Методические указания к выполнению самостоятельной работы по дисциплине «Сопротивление материалов»/ Сост. З.А. Наседкина, А.В. Песков - ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, 2014. 45 с.
ПРИЛОЖЕНИЕ 1
Сортамент прокатной стали ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНО - ГРАФИЧЕСКИХ РАБОТ При изучении курса «Сопротивление материалов» студенты выполняют расчетно-графические работы, состоящие из контрольных задач по основным разделам изучаемого курса. Количество расчетно-графических работ и задач в них определяется учебными планами по соответствующим специальностям. Контрольные задачи имеют индивидуальный характер: расчетные схемы и числовые данные для каждой задачи выбираются по шифру, состоящему из шести цифр. В зависимости от задания используются все шесть цифр шифра или только несколько цифр шифра. Шифр определяется по первым буквам фамилии, имени, отчества студента в зависимости от кодов этих букв, приведенных в таблице.
Задания выполняются на листах бумаги формата А4 (210x297), а чертежи к ним (с обязательным соблюдением масштаба) на миллиметровой бумаге того же формата. Обложка работы оформляется по образцу, приведенному в приложении 4. Перед выполнением каждого задания выписываются условия с исходными данными и составляется в масштабе чертеж, на котором указываются численные значения заданных величин. Все этапы решения нумеруются в соответствие с пунктами, указанными в условии, и снабжаются кратким пояснением. При расчете вначале выписываются используемые формулы с применением общепринятых буквенных обозначений, затем подставляются исходные данные вместо буквенных обозначений в той же последовательности и после этого производятся требуемые математические вычисления. Все численные расчеты требуется проводить в системе СИ. Окончательные результаты с обязательным указанием размерности в Международной системе СИ выделяются (подчеркиваются или берутся в рамки). После выполнения расчетно-графические работы предъявляются преподавателю для защиты не позднее срока, предусмотренного учебным планом. Примечание: Студент должен выбрать тип задачи и размеры в соответствии со своим шифром. Для этого следует написать шифр, а под ним буквы алфавита в определенном порядке. Например:
В таблице буквы стоят в конце колонок с соответствующими данными к задаче. Цифры, стоящие выше букв, показывают, из какой строки следует выбрать нужный параметр. Методические указания предназначены в помощь студентам машиностроительных специальностей при их самостоятельной работе над типовыми расчетами. В данной работе изложены методические указания по выполнению расчетно-графических работ для студентов по разделам: сдвиг, напряженное и деформированное состояние в точке, кручение стержня с круглым поперечным сечением (определение внутренних усилий, расчеты на прочность и жесткость: определение напряжений, деформаций, перемещений,). геометрические характеристики плоских сечений. Приводятся примеры решения типовых задач, а также задания для выполнения контрольных и расчетно-графических работ.
СДВИГ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 Например, студент Иванов Николай Петрович. В соответствие с кодами букв (И - 31, Н – 71, П - 59), взятыми из таблицы, составляется индивидуальный шифр - 317159.
Например, студент Иванов Николай Петрович. В соответствие с кодами букв (И - 31, Н – 71, П - 59), взятыми из таблицы, составляется индивидуальный шифр - 317159.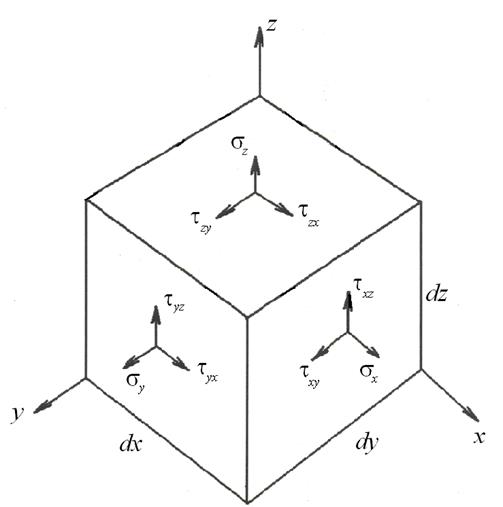

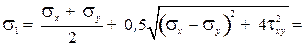
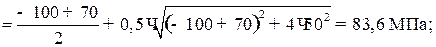

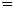

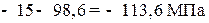 .
.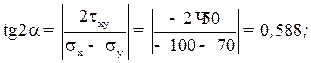
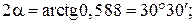
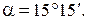
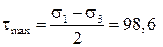 МПа.
МПа.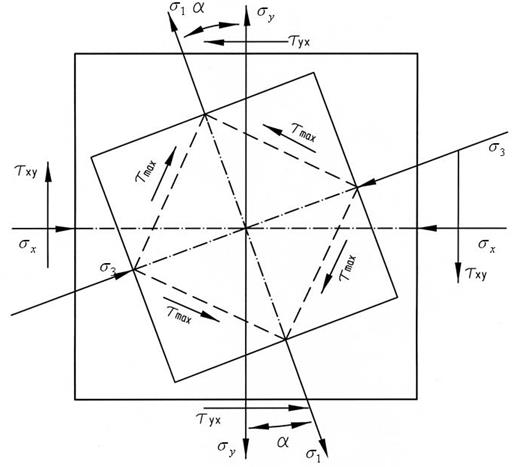
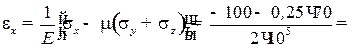



 .
. МПа.
МПа.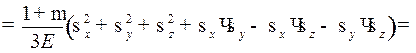
 МПа (Н/мм2).
МПа (Н/мм2). .
.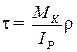 ,
,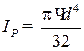 (прил. 4);
(прил. 4);
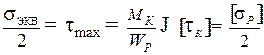 ,
,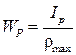 – геометрическая характеристика прочности при кручении, называемая полярным моментом сопротивления, м3;
– геометрическая характеристика прочности при кручении, называемая полярным моментом сопротивления, м3;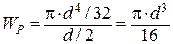 .
.
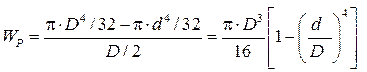 .
.
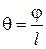 .
.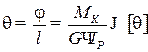 ,
, ,
,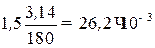 рад/м.
рад/м.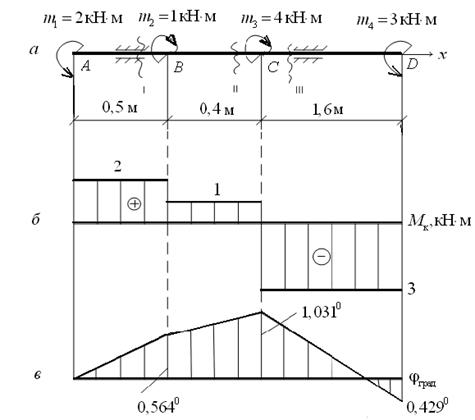
 ,
,  .
.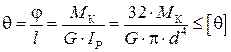 ,
, .
.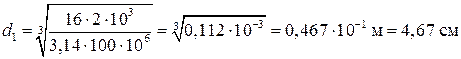 ;
;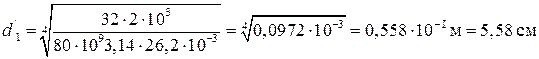 .
. ;
;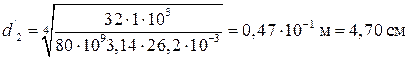 .
. .
.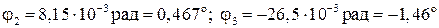 .
.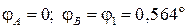 ;
;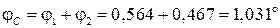 .
.