Напряженное и деформированное

СОСТОЯНИЕ В ТОЧКЕ

 

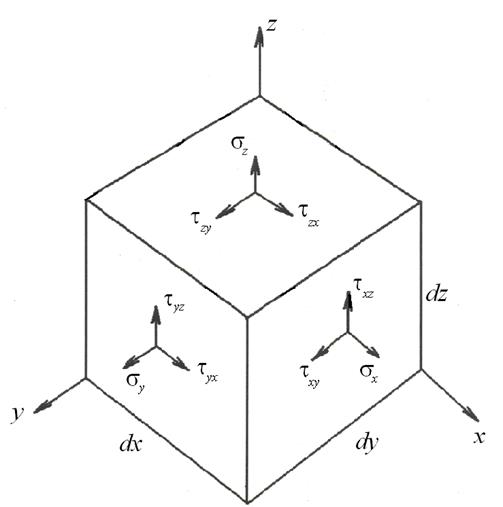
Для исследования напряженного состояния в точке деформируемого тела в ее окрестности выделяют элементарный объем в виде прямо­угольного параллелепипеда (рис. 2).

В общем случае деформирования напряженное состояние в точке характеризуется девятью величинами: тремя нормальными напряжениями σ _x, σ _y и σ _z и шестью касательными напряжениями – τ _xy, τ _xz, τ _yz, τ _zx, τ _yx, τ _zy.

Вследствие закона парности касатель­ных напряжений (τ _yz = τ _zy, τ _zx = = τ _xz, τ _xy = τ _yx) число независимых компонентов уменьшается до шести.

 

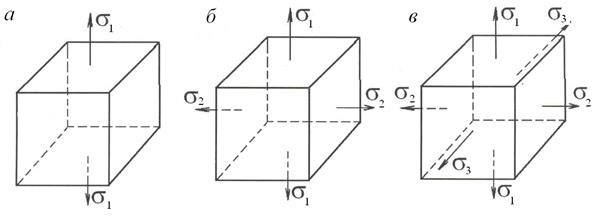
Рис. 2. Объемное напряженное состояние

Исследование напряженного состояния включает определение напряжений по произвольной площадке, проходящей через данную точку, а также положение главных площадок и значений главных нормальных напряжений. Среди бесконечно большого числа площадок, проходящих через данную точку тела, всегда найдутся по крайней мере три взаимно перпендикулярные площадки, на которых касательные напряжения отсутствуют. Такие площадки носят название главных площадок, а нормальные напряжения на них – главных норма­льных напряжений. Напряженное состояние в любой точке можно свести к растяжению или сжатию по одному, двум или трем взаимно перпендикулярным направлениям. В зависимости от этого различают линейное, пло­ское и объемное напряженное состояние (рис. 3).

 

 

Рис. 3. Виды напряженного состояния:

а – линейное; б – плоское; в – объемное

 

Очень важно уметь определять значения главных нормальных напряжений в случае плоского напряженного состояния, которое наиболее часто встречается в брусе, подвергающемся действию изгибающих, скручивающих и растягивающих нагрузок, а также в тонкостенных оболочках.

 

Пример 1

 

Исследовать плоское напряженное состояние стального кубика

(рис. 4, а).

Рис. 4. Hормальные и касательные напряжения по граням кубика:

а – направления напряжений для исследуемого напряженного состояния;

б – положительные направления напряжений

Абсолютные величины напряжений (см. рис. 4, а):

σ _x = 100 МПа; σ _y = 70 МПа; τ _xy = τ _yx = 50 МПа; Е = 2 ·10⁵ МПа; μ = 0,25.

Прежде всего установим знаки нормальных и касательных напряжений, показанных на рис. 4, а. Положительные направления

нормальных напряжений σ _x, σ _y и касательных напряжений τ _xy = τ _yx показаны на рис. 4, б. Нормальные растягивающие напряжения принято брать со знаком плюс, а сжимающие – со знаком минус. Следовательно, σ _x = –100 МПа и σ _y = 70 МПа, τ _xy = –50 МПа.

Определение главных напряжений. Наибольшее σ₁:

наименьшее из главных напряжений σ₂ :

 

.

Определение направления главных площадок. Угол наклона нормали главной площадки к оси X определяется по формуле

 

Знак касательных напряжений и угла α можно неустанавливать, если пользоваться следующим правилом для определения ориентации главных площадок.

Главные площадки, на которых действует наибольшее из главных напряжений σ_1, получаются поворотом на угол α тех из исходных площадок, на которых действует большее (по алгебраической величине) из исходных напряжений σ _x, σ _y. В нашем примере такими исходными площадками будут площадки, где действует нормальное напряжение σ _y, так как σ _y > σ _x.

Направление поворота указывает стрелка касательного напряжения на исходной площадке (рис. 5). Вторая пара главных площадок перпендикулярна найденным.

Определение максимальных касательных напряжений:

 

МПа.

 

Эти напряжения действуют на площадках, наклоненных под углом 45° к главным, и направлены в сторону σ₁ (см. рис. 5).

 

 

 

Рис. 5. Расположение главных площадок

 

Определение относительных деформаций ε _x, ε _y, ε _z:

 

Обратите внимание на то, что при σ _z = 0 ε _z ≠ 0, т.е. при от­сутствии напряжения по оси Z деформация в этом направлении имеет место.

 

Определение относительного изменения объема θ:

.

Определение удельной потенциальной энергии деформаций. Потен- циальная энергия изменения объема U _об:

 

U _об МПа.

 

Потенциальная энергия изменения формы U _ф:

U _ф

МПа (Н/мм²).

Полная энергия U:

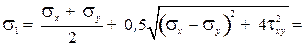
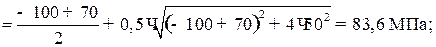
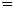
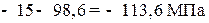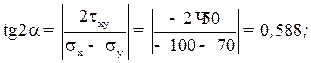
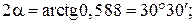
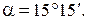
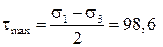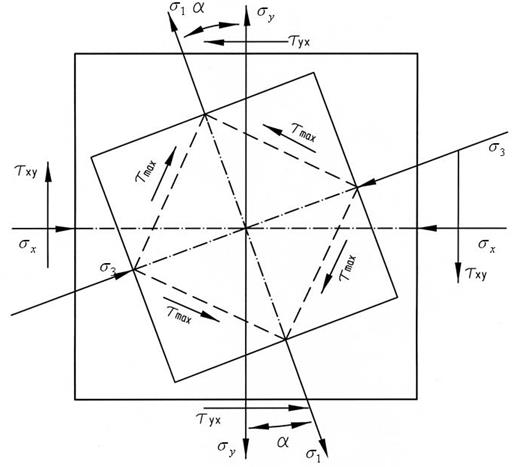
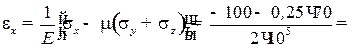
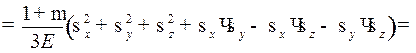
U = U _об + U _ф = 46·10^–3 = 46·10^–3 МПа (Н/мм²).