
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деформации и напряжения при сдвигеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Пусть на короткий и толстый брус KСDВ длиной ∆ s,заделанный одним концом, действует поперечная сила F, приложенная в крайнем сечении этого бруса (рис. 1).
Рис. 1. Деформации и напряжения при сдвиге
Вследствие малой длины бруса пренебрегаем незначительным искривлением его граней KС и BD, тогда деформация бруса под действием силы F выразится в смещении (сдвиге) грани CD относительно грани KВ. Величина перемещения СС 1(или DD 1 ) называется абсолютным или полным сдвигом. Из треугольника KСС 1видно, что при изменении длины бруса ∆ s будет изменяться и величина полного сдвига СС 1. Для получения деформации сдвига, не зависящей от длины ∆ s, введем понятие об относительном сдвиге по аналогии с понятием относительной продольной деформации ε. Относительным сдвигом будем называть величину сдвига, приходящуюся на единицу длины бруса, или частное от деления полного сдвига СС 1на длину бруса ∆s:
Здесь tgγ приравнен углу γ ввиду его малости. Сопоставляя деформацию сдвига с деформацией растяжения (сжатия), отметим, что первая из них характеризуется относительным сдвигом γ, а вторая — относительной продольной деформацией ε, К этим двум основным видам деформаций может быть приведена любая сложная деформация тела. Проводя мысленно сечение 1—1 (рис. 1) и рассматривая правую отсеченную часть бруса, замечаем, что уравновесить внешнюю силу F могут только внутренние силы, расположенные в плоскости сечения. Это значит, что при сдвиге во всех сечениях типа 1—1 возникают только касательные напряжения τ. Распределение этих напряжений по высоте сечения не будет равномерным, но для решения многих практических задач на сдвиг можно допустить, что касательные напряжения распределяются равномерно по всей площади сечения А (рис. 1). При этом допущении равнодействующая всех внутренних касательных сил будет τ∙ А. Приравнивая нулю сумму проекций всех сил, действующих на правую отсеченную часть бруса, получим τ∙ А − F = 0 или τ = Несмотря на внешнее сходство этой формулы с известной форму лой σ = необходимо помнить, что равномерный характер распределения нормальных напряжений а по всему сечению является достаточно точным и подтверждается опытом, а равномерность распределения касательных напряжений τ является условным, упрощающим расчеты допущением. В теории изгиба будет показано, что касательные напряжения τ распределяются по высоте сечения далеко неравномерно, и формула (23) дает только среднее значение этих напряжений. Любое сложное напряженное состояние тела всегда можно привести к двум основным видам напряжений: нормальному σ и касательному τ. Первому из них соответствует линейная относительная деформация ε, а второму — угловая γ. Опыты подтверждают, что закон Гука справедлив и при сдвиге, если сдвигающая поперечная сила F не превосходит определенного предела. По аналогии с формулой для нормальных напряжений σ при растяжении и сжатии σ = Е ∙ε напишем закон Гука при сдвиге τ = G ∙ γ(4) Читается он так: касательные напряжения прямо пропорциональны относительному сдвигу. Здесь G — коэффициент пропорциональности, называемый модулем упругости при сдвиге или модулем поперечной упругости. Этот модуль, так же как и модуль продольной упругости Е, характеризует физические свойства материала. Определяется он опытным путем и является мерой сопротивляемости материала при сдвиге: чем больше величина G, тем меньше деформация сдвига γ. В сопротивлении материалов, как правило, рассматриваются твердые однородные изотропные тела, т. е. такие, у которых упругие свойства во всех точках и по всем направлениям одинаковы. Упругие свойства однородных и изотропных тел вполне определяются тремя известными характеристиками: 1) коэффициентом Пуассона μ, выражающим зависимость между 2) модулем продольной упругости Е, характеризующим степень 3) модулем поперечной упругости G, характеризующим степень Между указанными тремя упругими характеристиками μ, E и G существует зависимость, которую приводим без доказательства
Эта формула дает возможность определить любую из трех физических характеристик, если две другие известны. Зависимость (5) подтверждается зкспериментально. Принимая коэффициент Пуассона μ = 0,25, получаем
Например, для стали Е = 2∙105 МПа, коэффициент Пуассона μ = 0,25 и по формуле (6) найдем, что модуль поперечной упругости G для стали равен: G = 0,4∙2∙105 = 8∙104 МПа. При других значениях μ будет другая зависимость между G и Е. Из формулы (5) также следует, что при любом значении μ (от 0 до 0,5) модуль поперечной упругости G будет меньше модуля продольной упругости Е. При численно равных значениях σ и τ деформация сдвига γ будет всегда больше продольной деформации ε во столько раз, во сколько раз Е больше G. Это видно из сравнения формул σ = Е ∙ε и τ = G ∙ γ; приравнивая правые части этих выражений, получаем Е ∙ε = G ∙ γ, откуда
Решение практических задач па сдвиг (срез, скалывание) обычно связано с необходимостью проверки на смятие. Смятием будем называть местное сжатие двух соприкасающихся тел (деталей конструкции). Явление сдвига в дереве называют скалыванием. Формулы для расчета на сдвиг и смятие аналогичны формулам для расчета на растяжение и сжатие: τ = σсм =
Здесь [τ] — допускаемое напряжение на сдвиг; [σсм] — допускаемое напряжение на смятие. Значения допускаемых напряжений [τ] и [σсм] приводятся в нормах проектирования конструкций.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |


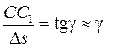
 (1)
(1) . (2)
. (2) . (5)
. (5) . (6)
. (6) . (7)
. (7)


