
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение совместности деформаций.Содержание книги
Поиск на нашем сайте
3) предел пропорциональности.
28. Точкой на диаграмме растяжения малоуглеродистой стали отмечен …
Предел текучести.
29. На диаграмме растяжения малоуглеродистой стали отмечен точкой...
2) предел прочности.
30. На диаграмме растяжения малоуглеродистой стали цифрой 2 отмечен …
3) предел упругости.
31. На диаграмме растяжения малоуглеродистой стали участок 0-1 называется …
3) участком упругой деформации.
32. На диаграмме растяжения малоуглеродистой стали участок 1–1′ называется …
Площадкой общей текучести.
33. На диаграмме растяжения малоуглеродистой стали участок 1–1′ называется …
1) участком упрочнения.
3) участком местной текучести.
35. Предел пропорциональности обозначается – … 3) sрr.
36. Предел упругости обозначается – … 2) sе.
37. Предел текучести обозначается –… 1) sy
38. Предел прочности обозначается –… 3) su.
39. Коэффициент Пуассона может принимать значения не больше величины … 2) 0,5
Растяжения малоуглеродистой стали.
41. На диаграмме растяжения малоуглеродистой стали по оси ε отмечена деформация 0–1 – …
3) пластическая.
42. На диаграмме растяжения малоуглеродистой стали по оси ε отмечена деформация 1–1′ – …
2) упругая.
43. На рисунке штриховой линией изображена...
44. На рисунке изображена диаграмма …
1) сжатия малоуглеродистой стали.
45. На рисунке изображена диаграмма …
Растяжение бронзы.
46. На диаграмме отмечен …
Условный предел текучести для цветных металлов.
47. Цифрой 2 обозначена диаграмма …
1) сжатие чугуна.
48. Цифрой 1 обозначена диаграмма …
2) растяжения чугуна.
49. На диаграмме сжатия чугуна su – это …
1) предел прочности при сжатии.
50. На диаграмме растяжения чугуна su – это …
2) предел прочности при растяжении.
51. На диаграмме сжатия малоуглеродистой стали обозначен …
1) предел пропорциональности. .
2) предел текучести.
53. На рисунке приведены диаграммы …
Геометрические характеристики плоских сечений
1. Геометрическая характеристика, определяемая интегралом Статическим моментом сечения относительно оси Х.
2. Геометрическая характеристика, определяемая интегралом Осевым моментом инерции сечения относительно оси У. 3. Геометрическая характеристика, определяемая интегралом Центробежным моментом инерции сечения.
4. Геометрическая характеристика, определяемая интегралом
Полярным моментом инерции сечения. 5. Осевой момент инерции прямоугольного сечения, если размер h перпендикулярен оси X, определяется по формуле … 2) 6. Осевой момент инерции круглого сечения определяется по формуле … 1)
7. Полярный момент инерции круглого сечения определяется по формуле … 3)
8. Полярный момент инерции кольцевого сечения определяется по формуле … 1)
9. Осевой момент инерции кольцевого сечения определяется по формуле … 1)
10. Геометрическая характеристика Wx – это … Момент сопротивления сечения при изгибе.
11. Геометрическая характеристика Wр – это …
Полярный момент сопротивления при кручении. 12. Полярный момент сопротивления круглого сечения при кручении определяется по формуле … 2) 13. Момент сопротивления круглого сечения при изгибе определяется по формуле … 3)
14. Момент сопротивления прямоугольного сечения при изгибе, если размер h перпендикулярен оси Х, определяется по формуле … 1) 15. Момент сопротивления кольцевого сечения при изгибе определяют по формуле … 1)
16. Полярный момент сопротивления кольцевого сечения при кручении определяют по формуле …
2)
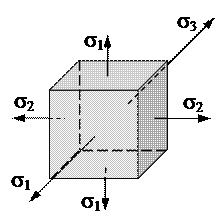
Основы напряженного состояния
1. Верно утверждение: …
1) s1=250 МПа; s2=120 МПа; s3=100 МПа.
Плоское
3. На рисунке представлено … напряженное состояние.
Линейное
4. На рисунке представлено … напряженное состояние.
Плоское
Объёмное
6. Максимальные и минимальные напряжения на главных площадках при плоском напряженном состоянии определяют по формуле … 1)
7. Площадка сдвига наклонена к главной площадке под углом …
2) a1 = 450
8. Экстремальные значения касательных напряжений на площадках сдвига определяют по формуле …
3)
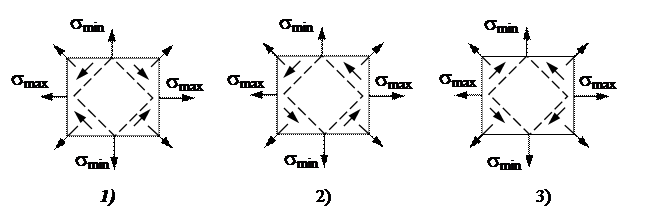
9. Направления напряжений на главных площадках при плоском напряженном состоянии указаны верно на рисунке ….
10. Величина относительного изменения объема вычисляется по формуле … 2)
11. Коэффициент Пуассона может принимать значения не больше величины … 3) 0,5.
12. Между тремя упругими постоянными Е, 1)
13. Коэффициент Пуассона для сталей имеет значения … . 3) ν = 0,25…0,3.
14. Коэффициент Пуассона может принимать не меньше значения величины … 1) 0 15. Положение главных площадок при плоском напряженном состоянии определяется по формуле … 2) 16. Интервал изменения значений коэффициента Пуассона: … 1)0£n£0,5
1. При чистом сдвиге в поперечном сечении возникают только … 1) нормальные напряжения. 2) касательные напряжения. 3) главные напряжения.
2. При сдвиге в поперечных сечениях бруса возникает … 1) изгибающий момент. 2) продольная сила. 3) поперечная сила.
3. Закон Гука при сдвиге записывается в виде … 1)
4. Произведение G·A называется … 1) жесткостью при сдвиге. 2) прочностью при сдвиге. 3) упругостью при сдвиге.
5. Модуль упругости материала G характеризует … 1) прочность при сдвиге. 2) жесткость при сдвиге. 3) упругость при сдвиге.
6. Условие прочности при срезе записывается в виде … 1) 2) 3)
7. Кручением называют такой вид нагружения вала, при котором … 1) в поперечных сечениях возникает крутящий момент Т и изгибающий момент М. 2) в поперечных сечениях возникает крутящий момент Т и нормальная сила N. 3) в поперечных сечениях возникает крутящий момент Т.
8. Для крутящих моментов принято правило знаков, представленное на рисунке ….
1) 2) 3)
9. В поперечном сечении круглого бруса при кручении возникают … напряжения. 1) касательные и нормальные 2) нормальные 3) касательные
10. Верна эпюра касательных напряжений
11. Касательные напряжения 1)
1) в середине вала. 2) на поверхности вала. 3) по всему сечению вала.
13. Максимальные касательные напряжения при кручении определяются по формуле … 1)
14. Геометрическая характеристика Wр называется …
1) моментом сопротивления при изгибе. 2) моментом инерции при кручении. 3) полярным моментом сопротивления при кручении.
15. Условие прочности при кручении записывается в виде … 1) 2) 3)
16. Полярный момент сопротивления при кручении для круглого вала определяется по формуле … 1)
17. Полярный момент сопротивления при кручении для кольцевого вала определяется по формуле … 1)
18. Допускаемое касательное напряжение при кручении определяется по формуле … 1)
19. Диаметр вала при кручении, исходя из расчета на прочность, определяется по формуле … 1)
20. Допускаемый из условия прочности крутящий момент определяется по формуле … 1)
21. Жёсткостью при кручении называется произведение … 1)
22. Угол закручивания вала на длине ℓ определяется по формуле … 1)
23. Относительный угол закручивания вала при кручении определяется по формуле … 1)
24. Условие жесткости при кручении записывается в виде … 1)
25. Допускаемый относительный угол закручивания для валов, работающих в обычных условиях, равен … 1)
26. Диаметр вала, исходя из расчёта на жесткость при кручении, определяется по формуле … 1) 27. Потенциальная энергия упругих деформаций при кручении вала определяется по формуле … 1)
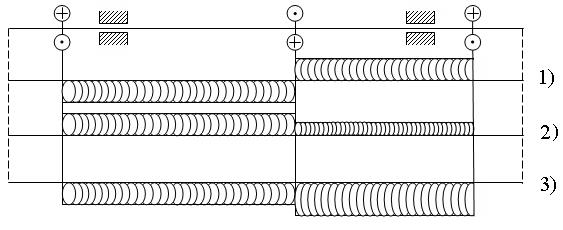
28. Верна эпюра крутящих моментов Т, представленная на рисунке ….
29. Стержень, работающий на кручение называется …
1) балкой. 2) брусом. 3) валом.
30. Модуль упругости второго рода для сталей принимает значения …
1) G=2,1 ×105 МПа. 2) G=8 ×104 МПа. 3) G=1 ×104 МПа.
31. Модуль упругости второго рода G измеряется в …
1) м. 2) Н. 3) Па.
Изгиб Оценка прочности
1. Напряжённое состояние в точке К представлено на рисунке ….
4. Напряжённое состояние в точке К представлено на рисунке ….
5. Напряжённое состояние в точке К представлено на рисунке ….
7. Напряжённое состояние в точке К представлено на рисунке ….
8. Напряжённое состояние в точке К представлено на рисунке ….
9. Напряжённое состояние в точке К представлено на рисунке ….
10. Напряжённое состояние в точке К представлено на рисунке ….
11. Напряжённое состояние в точке К представлено на рисунке ….
13. Напряжённое состояние в точке К представлено на рисунке ….
14. Напряжённое состояние в точке К представлено на рисунке ….
16. Напряжённое состояние в точке К представлено на рисунке ….
17. Напряжённое состояние в точке К представлено на рисунке ….
18. Эпюра поперечных сил Q верна на рисунке ….
19. Эпюра поперечных сил Q верна на рисунке ….
20. Эпюра поперечных сил Q верна на рисунке ….
24. Эпюра поперечных сил Q верна на рисунке ….
1) 2) 3) 4)
27. Эпюра поперечных сил Q верна на рисунке ….
28. Эпюра поперечных сил Q верна на рисунке ….
29. Эпюра поперечных сил Q верна на рисунке ….
30. Эпюра поперечных сил Q верна на рисунке ….
33. Эпюра поперечных сил Q верна на рисунке ….
37. Эпюра поперечных сил Q верна на рисунке ….
38. Эпюра поперечных сил Q верна на рисунке ….
1) 2) 3) 4)
39. Эпюра изгибающих моментов М верна на рисунке ….
40. Эпюра изгибающих моментов М верна на рисунке ….
41. Эпюра изгибающих моментов М верна на рисунке ….
42. Эпюра изгибающих моментов М верна на рисунке ….
43. Эпюра изгибающих моментов М верна на рисунке ….
44. Эпюра изгибающих моментов М верна на рисунке ….
45. Эпюра изгибающих моментов М верна на рисунке ….
46. Эпюра изгибающих моментов М верна на рисунке ….
48. Эпюра изгибающих моментов М верна на рисунке ….
49. Эпюра изгибающих моментов М верна на рисунке ….
50. Эпюра изгибающих моментов М верна на рисунке ….
51. Эпюра изгибающих моментов М верна на рисунке ….
53. Эпюра изгибающих моментов М верна на рисунке ….
54. Эпюра изгибающих моментов М верна на рисунке ….
56. Эпюра изгибающих моментов М верна на рисунке ….
57. Эпюра изгибающих моментов М верна на рисунке ….
58. Эпюра изгибающих моментов М верна на рисунке ….
59. Эпюра изгибающих моментов М верна на рисунке ….
60. Эпюра изгибающих моментов М верна на рисунке ….
61. Эпюра изгибающих моментов М верна на рисунке ….
62. Если длина балки ℓ и интенсивность распределённой нагрузки q удвоятся каждая, то напряжение σmax увеличится в …
1) 2 раза. 2) 8 раз. 3) 16 раз. 4) 32 раза.
Расчётные формулы.
63. Если размеры поперечного сечения при изгибе прямоугольной балки удвоить, то напряжение σmax уменьшится в …
1) 2 раза. 2) 16 раз. 3) 8 раз. 4) 0,5 раза.
Расчётные формулы.
64. Если М и диаметр круглой балки уменьшить вдвое, то напряжение σmax при изгибе увеличится в …
1) 2 раза. 2) 4 раза. 3) 8 раз. 4) 0,5 раза.
Расчётные формулы.
65. Если стороны b и h прямоугольного сечения удвоить каждую, то напряжение smax уменьшится в …
1) 8 раз. 2) 4 раза. 3) 3 раза. 4) 1 раз.
Расчётные формулы.
66. Если в сечении действует изгибающий момент М, то правильная эпюра s от z представлена на рисунке ….
67. Если сторона квадратной балки b уменьшится вдвое, то напряжение smax при изгибе увеличится в …
1) 2 раза. 2) 4 раза. 3) 8 раз. 4) 16 раз.
Расчётные формулы.
69. Если диаметр круглой балки уменьшится вдвое, то напряжение smax при изгибе увеличится в …
1) 2 раза. 2) 4 раза. 3) 8 раз. 4) 16 раз.
Расчётные формулы.
70. Эпюра касательных напряжений t при поперечном изгибе балки верна на рисунке ….
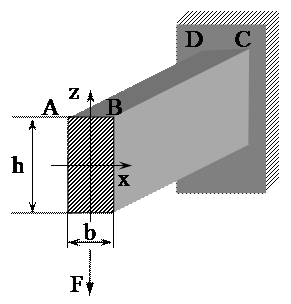
71. Если высоту сечения балки h увеличить вдвое, то величина нормального напряжения на поверхности ABCD прямоугольной балки …
1) уменьшится в 2 раза. 2) увеличится в 4 раза. 3) уменьшится в 4 раза. 4) останется без изменения.
Расчётные формулы.
72. Нормальное напряжение σmax определяется по формуле …
1)
73. Если сторона квадратной балки h уменьшится вдвое, то напряжение smax при изгибе увеличится в …
1) 2 раза. 2) 4 раза. 3) 8 раз. 4) 16 раз.
Расчётные формулы.
74. Эпюра касательных напряжений t от поперечной силы Q верна на рисунке ….
1) s. 2) t. 3) s и t.
76. Эпюра нормальных напряжений σ от изгибающего момента М верна на рисунке ….
77. Наибольшее касательное напряжение – в точке …
1) 1. 2) 2. 3) 3. 4) 4.
78. Наибольшее нормальное напряжение σmax определяется по формуле …
1) 3)
Расчётные формулы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.80.252 (0.014 с.) |

 27. На диаграмме растяжения малоуглеродистой стали точкой А отмечен …
27. На диаграмме растяжения малоуглеродистой стали точкой А отмечен …

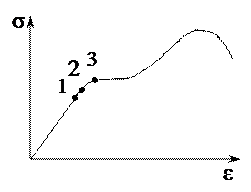
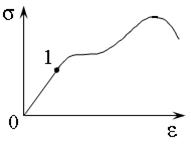


 34. На диаграмме растяжения малоуглеродистой стали участок 1–1′ называется …
34. На диаграмме растяжения малоуглеродистой стали участок 1–1′ называется … 40. На рисунке приведена диаграмма …
40. На рисунке приведена диаграмма …




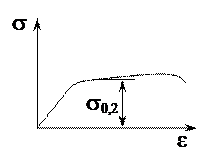





 52. На диаграмме сжатия малоуглеродистой стали обозначен …
52. На диаграмме сжатия малоуглеродистой стали обозначен …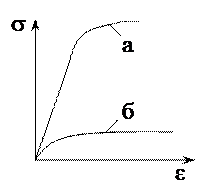
 , называется …
, называется … , называется …
, называется … , называется …
, называется …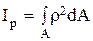 , называется …
, называется …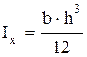 .
.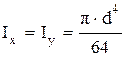 .
. .
. .
. .
. .
.
 .
.
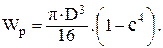

 2. На рисунке представлено … напряженное состояние.
2. На рисунке представлено … напряженное состояние.

 5. На рисунке представлено … напряжённое состояние.
5. На рисунке представлено … напряжённое состояние.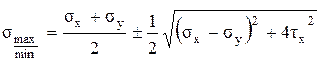 .
.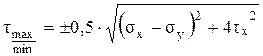 .
.
 .
. , G существует зависимость …
, G существует зависимость …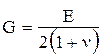 .
.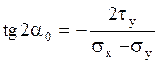 .
.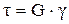 . 2)
. 2) 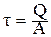 . 3)
. 3) 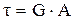 .
. .
.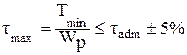 .
. .
.
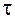 , представленная на рисунке ….
, представленная на рисунке ….
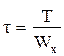 . 2)
. 2)  . 3)
. 3) 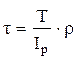 .
.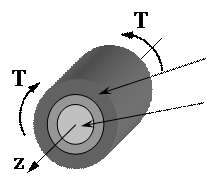 12. Наиболее нагруженные точки при кручении находятся …
12. Наиболее нагруженные точки при кручении находятся …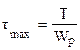 . 2)
. 2) 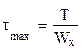 . 3)
. 3) 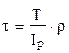 .
.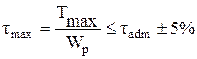 .
. .
. .
.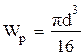 . 2)
. 2) 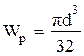 . 3)
. 3) 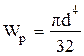 .
.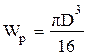 . 2)
. 2) 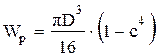 . 3)
. 3) 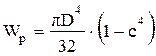 .
.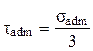 . 2)
. 2) 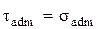 . 3)
. 3) 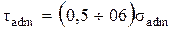 .
. . 2)
. 2) 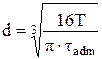 . 3)
. 3) 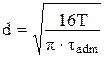 .
.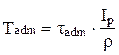 . 2)
. 2) 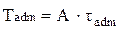 . 3)
. 3) 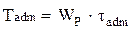 .
. . 2)
. 2) 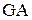 . 3)
. 3)  .
.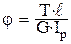 . 2)
. 2) 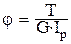 . 3)
. 3)  .
. . 2)
. 2) 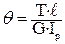 . 3)
. 3)  .
.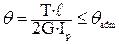 . 2)
. 2) 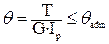 . 3)
. 3) 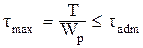 .
.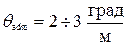 . 2)
. 2) 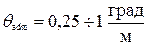 . 3)
. 3)  .
.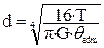 . 2)
. 2) 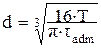 . 3)
. 3) 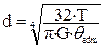 .
. . 2)
. 2) 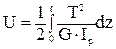 . 3)
. 3) 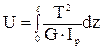 .
.
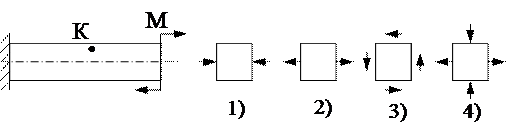
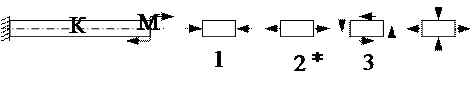
 2. Напряжённое состояние в точке К представлено на рисунке ….
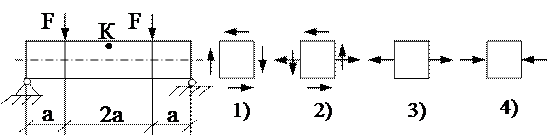
2. Напряжённое состояние в точке К представлено на рисунке ….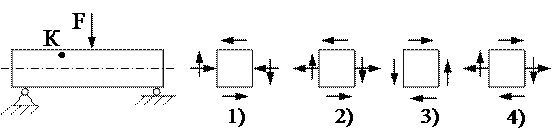 3. Напряжённое состояние в точке К представлено на рисунке ….
3. Напряжённое состояние в точке К представлено на рисунке ….
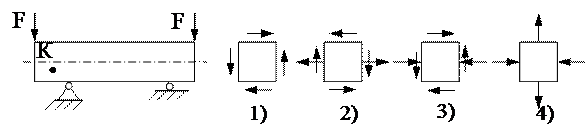 6. Напряжённое состояние в точке К представлено на рисунке ….
6. Напряжённое состояние в точке К представлено на рисунке ….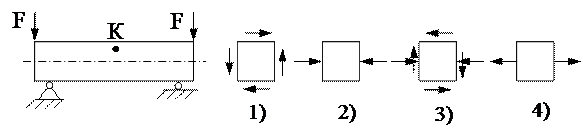
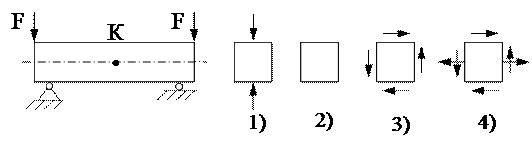
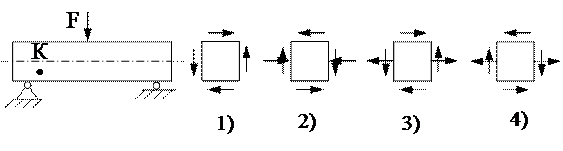
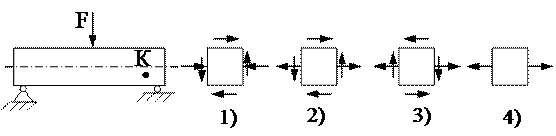
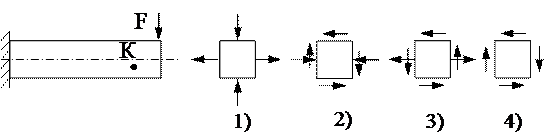
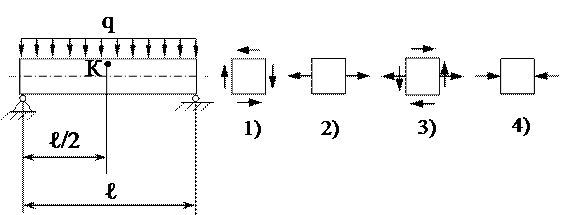 12. Напряжённое состояние в точке К представлено на рисунке ….
12. Напряжённое состояние в точке К представлено на рисунке ….
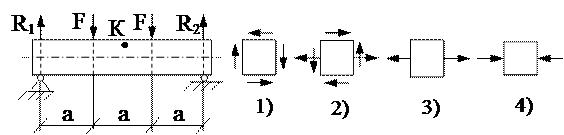
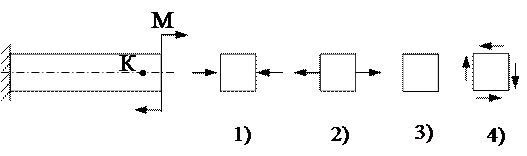 15. Напряжённое состояние в точке К представлено на рисунке ….
15. Напряжённое состояние в точке К представлено на рисунке ….
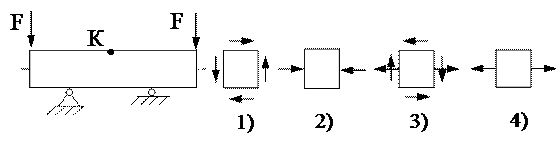

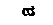


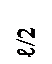
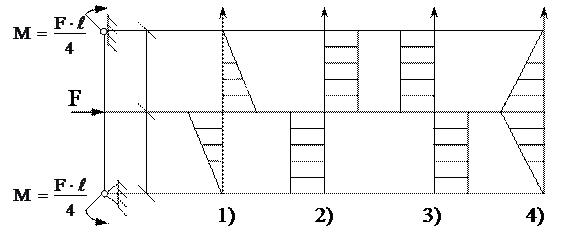

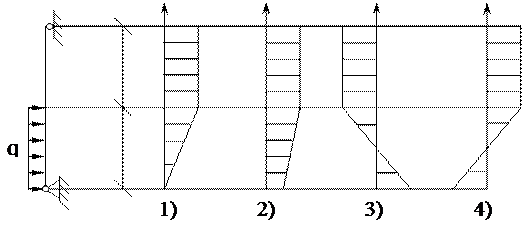

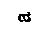
 21. Эпюра поперечных сил Q верна на рисунке ….
21. Эпюра поперечных сил Q верна на рисунке ….
 22. Эпюра поперечных сил Q верна на рисунке ….
22. Эпюра поперечных сил Q верна на рисунке ….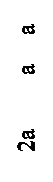
 23. Эпюра поперечных сил Q верна на рисунке ….
23. Эпюра поперечных сил Q верна на рисунке ….
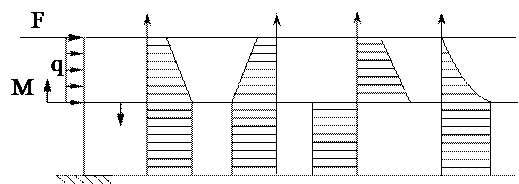 25. Эпюра поперечных сил Q верна на рисунке ….
25. Эпюра поперечных сил Q верна на рисунке ….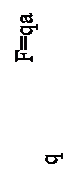
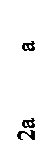
 26. Эпюра поперечных сил Q верна на рисунке ….
26. Эпюра поперечных сил Q верна на рисунке ….


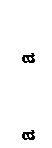


 31. Эпюра поперечных сил Q верна на рисунке ….
31. Эпюра поперечных сил Q верна на рисунке ….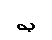
 32. Эпюра поперечных сил Q верна на рисунке … (M1=M2).
32. Эпюра поперечных сил Q верна на рисунке … (M1=M2).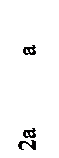


 34. Эпюра поперечных сил Q верна на рисунке ….
34. Эпюра поперечных сил Q верна на рисунке ….
 35. Эпюра поперечных сил Q верна на рисунке ….
35. Эпюра поперечных сил Q верна на рисунке …. 36. Эпюра поперечных сил Q верна на рисунке ….
36. Эпюра поперечных сил Q верна на рисунке ….
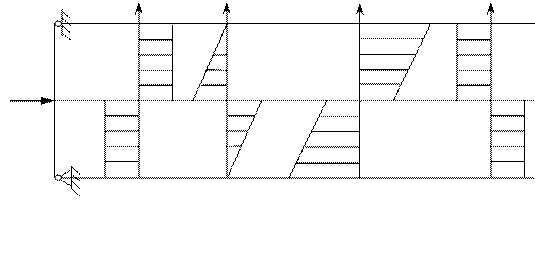


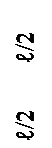

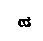
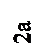

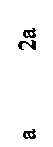


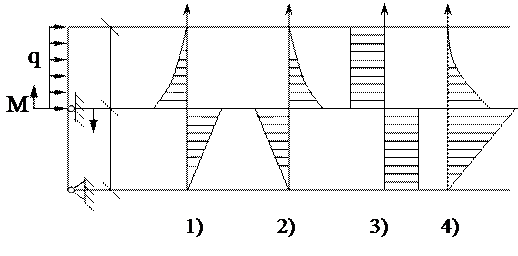


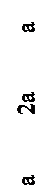


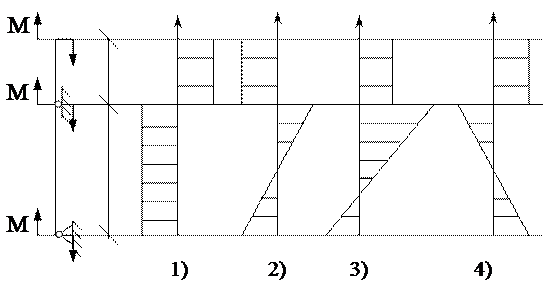 47. Эпюра изгибающих моментов М верна на рисунке ….
47. Эпюра изгибающих моментов М верна на рисунке ….





 52. Эпюра изгибающих моментов М верна на рисунке ….
52. Эпюра изгибающих моментов М верна на рисунке ….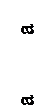



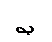
 55. Эпюра изгибающих моментов М верна на рисунке … (M1=M2).
55. Эпюра изгибающих моментов М верна на рисунке … (M1=M2).

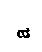







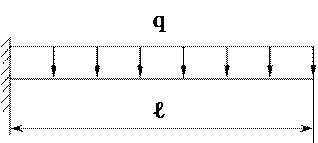
 (если ℓ и q удвоятся, то Мmax увеличится в восемь раз).
(если ℓ и q удвоятся, то Мmax увеличится в восемь раз).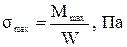 (если Мmax увеличится в восемь раз, то σmax увеличится в восемь раз).
(если Мmax увеличится в восемь раз, то σmax увеличится в восемь раз). (если увеличить в два раза размер b и увеличить в два раза размер h, то момент сопротивления W увеличится в восемь раз).
(если увеличить в два раза размер b и увеличить в два раза размер h, то момент сопротивления W увеличится в восемь раз).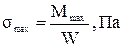 (если момент сопротивления W увеличится в восемь раз, то σmax уменьшится в восемь раз).
(если момент сопротивления W увеличится в восемь раз, то σmax уменьшится в восемь раз).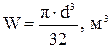 (если диаметр уменьшить в два раза, то момент сопротивления W уменьшится в восемь раз).
(если диаметр уменьшить в два раза, то момент сопротивления W уменьшится в восемь раз).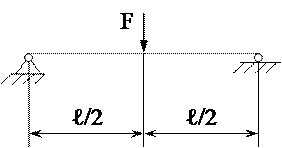
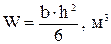 (если увеличить в два раза размер b и увеличить в два раза размер h, то момент сопротивления W увеличится в восемь раз).
(если увеличить в два раза размер b и увеличить в два раза размер h, то момент сопротивления W увеличится в восемь раз).
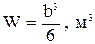 (если уменьшить в два раза размер b, то момент сопротивления W уменьшится в восемь раз).
(если уменьшить в два раза размер b, то момент сопротивления W уменьшится в восемь раз).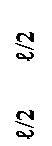
 68. Эпюра нормальных напряжений smax верна на рисунке ….
68. Эпюра нормальных напряжений smax верна на рисунке ….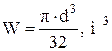 (если диаметр круглой балки уменьшится вдвое, то момент сопротивления сечения уменьшится в восемь раз).
(если диаметр круглой балки уменьшится вдвое, то момент сопротивления сечения уменьшится в восемь раз).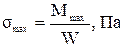 (если момент сопротивления сечения уменьшится в восемь раз, то напряжение smax увеличится в восемь раз).
(если момент сопротивления сечения уменьшится в восемь раз, то напряжение smax увеличится в восемь раз).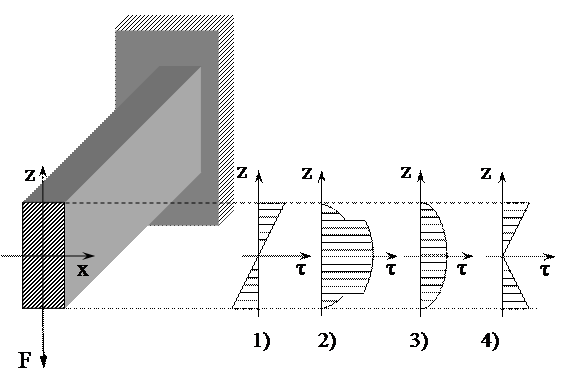
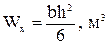 (если высоту сечения балки h увеличить вдвое, то момент сопротивления Wx увеличится в четыре раза).
(если высоту сечения балки h увеличить вдвое, то момент сопротивления Wx увеличится в четыре раза). (если момент сопротивления Wx увеличится в четыре раза, то напряжение σmax уменьшится в четыре раза).
(если момент сопротивления Wx увеличится в четыре раза, то напряжение σmax уменьшится в четыре раза).
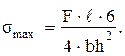 2)
2)  3)
3)  4)
4) 
 (если сторона квадратной балки h уменьшится вдвое, то момент сопротивления W уменьшится в восемь раз).
(если сторона квадратной балки h уменьшится вдвое, то момент сопротивления W уменьшится в восемь раз).
 75. При действии распределенной нагрузки возникают напряжения …
75. При действии распределенной нагрузки возникают напряжения …

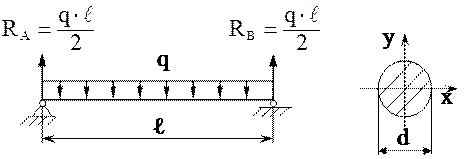
 2)
2) 
 4)
4) 
 (максимальный изгибающий момент посередине балки).
(максимальный изгибающий момент посередине балки). (момент сопротивления изгибу круглого сечения).
(момент сопротивления изгибу круглого сечения). (максимальное напряжени
(максимальное напряжени 


