Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача об оптимальной корзине продуктов (задачи о диете, задачи о составлении смеси).Содержание книги
Поиск на нашем сайте
Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г = 0.5 кг. Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определённым требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
Математическая формулировка задачи. Введём следующие обозначения: Общий вес смеси, еженедельно расходуемый на кормление цыплят: 20 000 х 0.5 = 10 000 кг. Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид: 0.38X1 + 0.001Х2 + 0.002Х3 ≥ 0.008 х 10 000, 0.09Х2 + 0.50Х3 ≥ 0.22 х 10 000, 0.02Х2+ 0.08Х3 ≤ 0.05 х 10 000. Окончательный вид математической формулировки задачи: min f(X) = 0.04 x1 + 0.15Х2 +0,40Х3 при ограничениях Х1+Х2+Х3= 10 000 0.38Х1 + 0.001Х2 + 0.002Х3 ≥ 80 0.09Х2+ 0.50Х3 ≥ 2200 0.02Х2+ 0.08Х3 ≤ 500 Xj > 0, j = 1, 2, 3 Задача о составлении рациона (задача о диете, задача о смесях) Имеется два вида продукции П1 и П2, содержащие питательные вещества S1, S2, S3, S4 (жиры, белки, углеводы, витамины). Содержание числа единиц питательных веществ в единице каждого вида продукции и необходимый минимум питательных веществ приведены в табл. 2. Таблица 2
Стоимость единицы продукции П1 и П2 соответственно равна 3 и 4 д.е. F = 3x1 + 4x2. (5) С учетом необходимого минимума питательных веществ составим систему ограничений. Рацион включает (x1 + 2x2) единиц питательного вещества S1, (3x1 + 2x2) единиц питательного вещества S2, (2x1 + x2) единиц питательного вещества S3 и (2x1 + 2x2) единиц питательного вещества S4. Так как содержание питательных веществ S1, S2, S3, S4 в рационе должно быть не менее 10, 8, 9, 11 единиц, соответственно, то получим систему ограничений неравенств:
Итак, экономико-математическая модель задачи: составить дневной рацион F=c1x1+c2x2+…+cnxn→(min) (7)
Замечание 2. В задаче составления рациона (диеты, кормовой смеси) могут использоваться ограничения не только по необходимому минимуму питательных веществ, но и по минимальному общему весу смеси.
при ограничениях: на общий расход смеси на питательность смеси на не отрицательность переменных xj≥0, j=1,2,…n, где xj – количество j-го сырья в смеси; n – количество видов сырья; m – количество питательных веществ; aij – количество i-го питательного вещества, содержащегося в единице j-го вида сырья; b1 – минимальное количество i-го питательного вещества, содержащегося в единице смеси; cj – стоимость единицы сырья j; q – минимальный общий вид смеси
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.187 (0.007 с.) |

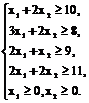
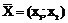 , удовлетворяющий системе ограничений (6), при котором функция (5) принимает минимальное значение.
, удовлетворяющий системе ограничений (6), при котором функция (5) принимает минимальное значение.