Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет временных параметров сетевого графика 2.2.1. Расчет критического путиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Почти в любой сети от исходного события до завершающего ведет несколько путей. Каждому пути соответствует последовательность каких-то работ. Путь в сети от исходного события до завершающего называется полным путем. Обозначается полый путь буквой L. Продолжительностью пути в сетевом графике называется время, необходимое для выполнения всех работ, лежащих на этом пути. Продолжительность полного пути обозначим t (L). Путь, имеющий наибольшую протяженность, называется критическим путем Замечание. В сети может быть несколько критических путей. Работы, лежащие на критическом пути, называются критическими. От их продолжительности зависит общий срок завершения всех работ. Некритические работы допускают некоторое запаздывание в их выполнении, которое не задержит сроков реализации всего проекта. Ранним сроком
Полный срок наступления события - время, при котором планируемый срок окончания проекта не меняется. Обозначается Замечание. Для завершающего события К поздний срок наступления совпадает с ранним, т. е.
При определении поздних сроков наступления события расчет ведут от завершающего события к исходному. Каждую вершину орграфа (событие сетевой модели) разобьем на 3 сектора: в нижнем проставляем номер события; в левом - ранний срок; в правом - поздний срок.
Резервы времени каждого события находятся по формуле:
Замечание. Для событий i, лежащих на критическом пути, ранние и поздние сроки наступления совпадают, т. е. Понятие ранних и поздних сроков наступления событий играют важную роль в процессе выполнения проекта. Если все события i наступают не позднее Если какое-то событие i наступает позднее Метод расчета сетевых графиков выполняется в четыре этапа: 1. Определение ранних сроков наступления событий 2. Нахождение критического пути 3. Определение поздних сроков наступления события 4. Определение резерва времени Замечание. Использование независимого резерва времени на i-й работе, которая его имеет, не влияет на ранние и поздние сроки совершения всех событий и работ сети. Его нельзя передать ни предшествующим, ни последующим работам. Оптимизация СМ выражается в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения. Для этого необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также всех «цепочек» пути. Более точным инструментом решения этой задачи, по сравнению с полным резервом, является коэффициент напряженности. Его можно вычислить по следующим формулам:
где t (
Коэффициент напряженности изменяется от 0 до 1. Чем ближе он к 1, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых На основе этого коэффициента все работы сетевого графика подразделяются на три группы: 1) 2) 0,6 < 3) В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ. Для этого необходимо все работы перевести в первую группу. Пример 1. Ставропольский кондитерский цех решил закупить новое оборудование. Исходные данные по основным операциям проекта представлены в таблице. Необходимо построить сетевую модель проекта, определить временные параметры модели, критический путь и проанализировать, как влияет на ход выполнения проекта задержка определенного типа оборудования на 12 часов.
Решение. Построим сетевую модель по условию задачи.
Работы Найдем ранние сроки наступления событий:
Найдем поздние сроки наступления событий для завершающего события 6
При поиске критических путей на сетевом графике будем использовать следующие условия его критичности: • необходимое условие - нулевые резервы событий, лежащих на критическом пути; • достаточное условие - нулевые полные резервы работ, лежащих на критическом пути. Согласно необходимому условию два полных пути сетевой модели могут быть критическими: L1 =1, 3, 4, 5, 6 и L2 =1, 4, 5, 6. Проверим достаточное условие критичности для работ (1, 3) и (1, 4)
Путь L2, начинающийся с работы (1, 4) не является критическим, так как минимум одна (1, 4) из его работ не является критической. Работа (1, 4) имеет не нулевой полный резерв, а значит, может быть задержана с выполнением, что недопустимо для критических работ. Таким образом, сетевая модель имеет единственный критический путь
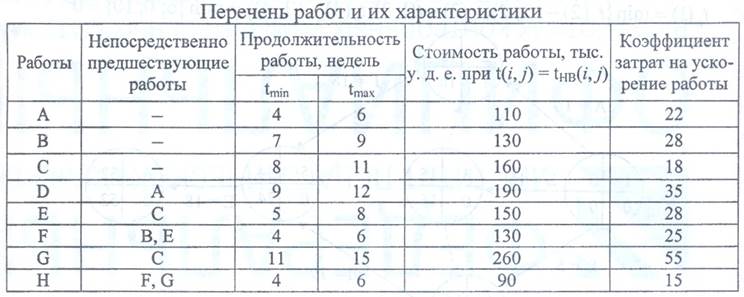
Работа А или (1, 2) не является критической, ее полный резерв равен 1 часу. Это означает, что при задержке работы в пределах 1 часа срок выполнения проекта не будет нарушен. Поэтому, если согласно условию работа А задержится на 12 часов, то весь проект задержится на 11 часов. Пример 2. Компания «АВC» реализует проекты серийного производства различных видов продукции. Каждый проект обеспечивает получение в неделю 100 тыс. у. д. е. дополнительной прибыли. Перечень работ и их характеристики представлены в таблице.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.011 с.) |

 . Протяженность критического пути обозначаем t (
. Протяженность критического пути обозначаем t (  .
. (j) свершения события j называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счет времени ведется от момента наступления начального события. Ранний срок начального события равен 0.
(j) свершения события j называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счет времени ведется от момента наступления начального события. Ранний срок начального события равен 0. 
 (i) - для i -гo события.
(i) - для i -гo события.
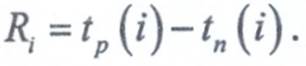
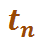 (i), то это значит, что проект осуществится не позднее установленного срока.
(i), то это значит, что проект осуществится не позднее установленного срока. события.
события.
 ) - продолжительность максимального пути, проходящего через работу (i, j);
) - продолжительность максимального пути, проходящего через работу (i, j); - продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.
- продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем. = 1.
= 1. (i,j) > 0,8 - напряженные;
(i,j) > 0,8 - напряженные;
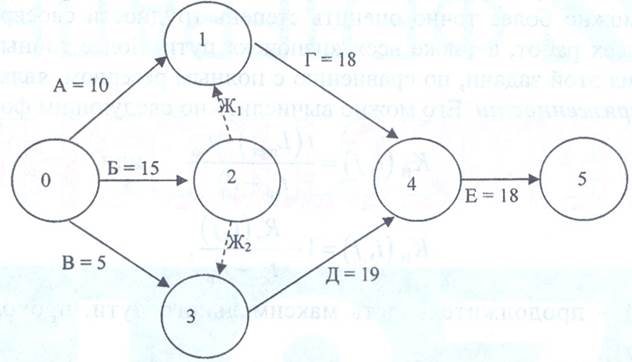
 и
и  введены для устранения параллельности работ Г и Д. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного собьпия и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляет одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.
введены для устранения параллельности работ Г и Д. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного собьпия и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляет одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.
 (3) - t (1, 3);
(3) - t (1, 3);

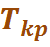 = 52 часа. За выполнением работ этого пути необходим особый контроль, так как любое увеличение их длительности нарушит срок выполнения проекта в целом.
= 52 часа. За выполнением работ этого пути необходим особый контроль, так как любое увеличение их длительности нарушит срок выполнения проекта в целом.