
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа - это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
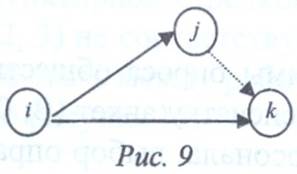
Работа - это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата. Фиктивная работа - это связь между результатами работ (событиями), не требующая затрат времени и ресурсов. Событие - это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ. Путь - это любая непрерывная последовательность (цепь) работ и событий. Критический путь - это путь, не имеющий резервов и включающий самые напряженные работы комплекса. Работы, расположенные на критическом пути, называются критическими. Все остальные работы являются некритическими (ненапряженными) и обладают резервами времени, которые позволяют передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ. При построении сетевых моделей необходимо соблюдать следующие правила: Сеть вычерчивается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером. 2. Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рис. 9).
3. В сети не должно быть тупиков, т. е. промежуточных событий, из которых не выходит ни одна работа (рис. 10).
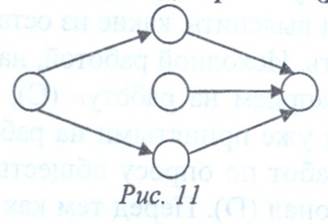
В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рис. 11).
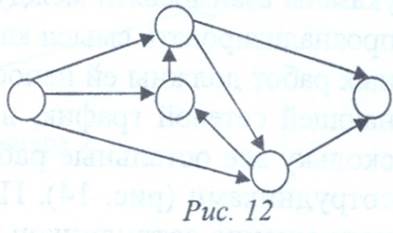
5. В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую цепь (рис. 12).
Если одно событие служит началом для двух или более работ, после завершения которых начинается выполнение следующей работы, то вводится штриховая стрелка (условная зависимость) и дополнительное событие со своим номером. 7. Если какие-то работы могут начинаться до полного завершения предыдущей работы, то ее следует разбить на части и считать каждую из них самостоятельной. Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события, которому дается номер 1. из исходного события 1 вычеркивают все исходящие из него работы, на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2. Затем вычерчивают работы, выходящие из события 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа, ему присваивается номер 3, и так продолжается до завершающего события. Пример нумерации сетевого графика показан на рисунке 13.
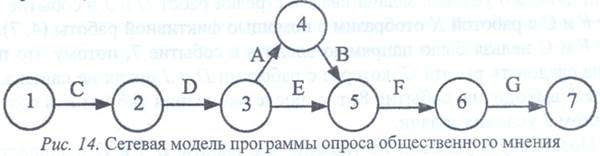
Продолжительность выполнения работ устанавливается на основании действующих нормативов или по экспертным оценкам специалистов. В первом случае временные оценки являются детерминированными (однозначными), во втором - стохастическими (вероятностными). Пример 1. Построить сетевую модель программы опроса общественного мнения, которая включает разработку (А; 1 день) и распечатку анкет (В; 0,5 дня), прием на работу (С; 2 дня) и обучение (D; 2 дня) персонала, выбор опрашиваемых лиц (Е; 2 дня), рассылку им анкет (F; 1 день) и анализ полученных данных (G; 5 дней). Решение. Из условия задачи нам известно содержание работ, но явно не указаны взаимосвязи между работами. Поэтому для их установления необходимо проанализировать смысл каждой конкретной работы и выяснить, какие из остальных работ должны ей непосредственно предшествовать. Исходной работой, начинающей сетевой график, в данном случае является «прием на работу» (С), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис. 14). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (D). Перед тем как разослать анкеты (F), их надо разработать (А), распечатать (В) и выбрать опрашиваемых лиц (Е), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (G), который нельзя выполнить без предварительной рассылки анкет (F). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис. 14).
Пример 2. Построить сетевую модель, включающую работы А, В, С,..., L, которая отображает следующее упорядочение работ: 1) А, В и С - исходные операции проекта; 2) А и В предшествуют D; 3) В предшествует Е, F и Н; 4) F и С предшествует G; 5) Е и Н предшествуют I и J; 6) С, D, F и J предшествуют К; 7) К предшествует L. Решение. В пункте 1 условия явно указано, что А, В и С являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2 условия означает, что стрелки работ А и В должны окончиться в одном событии, из которого выйдет стрелка работы D. Но поскольку стрелки работ А и В также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей. Для ее устранения введем дополнительное событие 2, в которое войдет работа В, после чего соединим события 2 и 3, в которые входят работы А и В, пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами В и D. Дальнейшее построение рассмотрим с помощью рисунка 15.
Согласно пункту 3 условия задачи, из события 2 выходят три стрелки работ Е, F и Н. Согласно пункту 4 условия задачи стрелки работ С и F должны войти в общее событие, из которого выйдет стрелка работы G. Проблема с параллельностью работ Е и Н (пункт 5 условия задачи) решается путем введения дополнительного события 5 и фиктивной работы (5, 6). для отображения в сетевой модели пункта 6 условия задачи введем стрелки работ D и J в событие 7, а связь работ F и С с работой К отобразим с помощью фиктивной работы (4,7). Стрелки работ F и С нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа G, которая с работами D и J никак не связана. Стрелка работы L выходит из события 8, т. е. после окончания работы К в соответствии с пунктом 7 условия задачи. Поскольку в условии не указано, что работы L, I и G предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события. Работы, лежащие на критическом пути, называются критическими. От их продолжительности зависит общий срок завершения всех работ. Некритические работы допускают некоторое запаздывание в их выполнении, которое не задержит сроков реализации всего проекта. Ранним сроком
Полный срок наступления события - время, при котором планируемый срок окончания проекта не меняется. Обозначается Замечание. Использование независимого резерва времени на i-й работе, которая его имеет, не влияет на ранние и поздние сроки совершения всех событий и работ сети. Его нельзя передать ни предшествующим, ни последующим работам. Оптимизация СМ выражается в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения. Для этого необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также всех «цепочек» пути. Более точным инструментом решения этой задачи, по сравнению с полным резервом, является коэффициент напряженности. Его можно вычислить по следующим формулам:
где t (
Коэффициент напряженности изменяется от 0 до 1. Чем ближе он к 1, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых На основе этого коэффициента все работы сетевого графика подразделяются на три группы: 1) 2) 0,6 < 3) Пример 1. Ставропольский кондитерский цех решил закупить новое оборудование. Исходные данные по основным операциям проекта представлены в таблице. Необходимо построить сетевую модель проекта, определить временные параметры модели, критический путь и проанализировать, как влияет на ход выполнения проекта задержка определенного типа оборудования на 12 часов.
Решение. Построим сетевую модель по условию задачи.
Работы Найдем ранние сроки наступления событий:
Найдем поздние сроки наступления событий для завершающего события 6
При поиске критических путей на сетевом графике будем использовать следующие условия его критичности: • необходимое условие - нулевые резервы событий, лежащих на критическом пути; • достаточное условие - нулевые полные резервы работ, лежащих на критическом пути. Согласно необходимому условию два полных пути сетевой модели могут быть критическими: L1 =1, 3, 4, 5, 6 и L2 =1, 4, 5, 6. Проверим достаточное условие критичности для работ (1, 3) и (1, 4)
Путь L2, начинающийся с работы (1, 4) не является критическим, так как минимум одна (1, 4) из его работ не является критической. Работа (1, 4) имеет не нулевой полный резерв, а значит, может быть задержана с выполнением, что недопустимо для критических работ. Таким образом, сетевая модель имеет единственный критический путь
Работа А или (1, 2) не является критической, ее полный резерв равен 1 часу. Это означает, что при задержке работы в пределах 1 часа срок выполнения проекта не будет нарушен. Поэтому, если согласно условию работа А задержится на 12 часов, то весь проект задержится на 11 часов. Пример 2. Компания «АВC» реализует проекты серийного производства различных видов продукции. Каждый проект обеспечивает получение в неделю 100 тыс. у. д. е. дополнительной прибыли. Перечень работ и их характеристики представлены в таблице.
Возможные полные пути I. 1 - 2 - 5. Длина: tНВ А + tHB D = 5,2 + 10,8 = 16. II. 1 - 3 - 6 - 5. Длина: tНВ В + tHB F+ tHB Н = 8,2 + 5,2 +5,2 = 18,6. III. 1 - 4 - 6 - 5. Длина: tНВ С+ tНВ G+ tHB Н = 9,8 + 13,4 + 5,2,= 28,4. IV. 1 - 4 - 3 - 6 - 5. Длина: tHB C+ tHB В+ tHB P+ tHB H= 9,8 + 6,8 + 5,2 + 5,2 = =27. Максимальная длина пути, равная 28,4 недели, соответствует пути III, на котором лежат работы С, G, Н. Следовательно, он является критическим. Пример. Рассмотрим сетевую модель с исходным событием О и завершающим событием 6.
Критические операции изображаются сплошными линиями. Отрезки времени, в пределах которых могут выполняться некритические операции, наносятся пунктирными линиями, показывающими, что календарные сроки этих операций можно выбрать в указанных пределах при условии сохранения отношений следования. На рисунке 18 показан календарный график, соответствующий примеру. Фиктивная операция (3, 4) не требует затрат времени, поэтому показана на графике вертикальным отрезком. Числа, проставленные над некритическими операциями, соответствуют их продолжительностям.
Роль полных и свободных резервов времени при выборе календарных сроков выполнения некритических операций объясняется двумя общими правилами: Правило 1. Если полный резерв равен свободному, то календарные сроки некритической операции можно выбрать в любой точке между ее ранним началом и поздним окончанием (пунктирные отрезки на рисунке 18). Правило 2. Если свободный резерв меньше полного, то срок начала некритической операции можно сдвинуть по отношению к ее раннему сроку начала не более чем на величину свободного резерва, не влияя при этом на выбор календарных сроков непосредственно следующих операций. В рассматриваемом примере правило 2 применимо только к операции (0, 1), а календарные сроки всех остальных операций выбираются по правилу 1. 2.2.3. График привязки (график Ганта) Для небольших проектов удобным дополнением к сетевому графику является линейный график (график Ганта). Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси - отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа (i, j) может выполняться только после того, как будут выполнены все предшествующие ей работы (k, i). При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта ( Из вышеприведенных соображений следует способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево): 1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие имеет номер завершающего события сети); 2) из всех работ сети (k, i), конечное событие которых i совпадает с начальным событием i работы (i, j), найденной в п. 1, выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j); 3) из всех работ сети (l, k), конечное событие которых k совпадает с начальным событием k работы (k, i), найденной в п. 2, выбрать и выписать ту, которая на графике вплотную примыкает к работе (k, i); 4) продолжать п. 3 до тех пор, пока не будет найдена исходная работа сети, т. е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1). Следует заметить, что если в сетевой модели несколько критических путей, то, выполняя вышеописанные действия, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критических путей. Тем не менее, такой способ хорош для учебных целей, поскольку дает понимание значения критических работ в сетевой модели и учит «читать» и понимать график привязки. Пример. По данным о кодах и длительностях работ в днях построить график привязки сетевой модели, определить критические пути и их длительность. Определить свободные и полные резервы каждой работы, отметить на графике привязки свободные резервы работ.
Решение. I. Поиск критических путей. 1) Построим график привязки (рис. 19).
2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис. 19) две работы (6, 7) и (3, 7), которые заканчиваются позже остальных в завершающем событии № 7. Записываем работы, определенные как критические справа налево. 3) Найдем критическую работу из (6, 7). Допишем слева найденную критическую работу (3, 6) к выражению
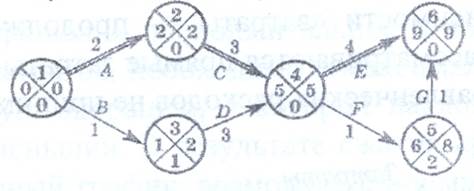
4) Найдем критическую работу из 5) Найдем критическую работу из (2, 3). С этой работы начинается критический путь 6) Аналогичный поиск работ критического пути В другой форме записи Стоимость выполнения каждой работы плюс дополнительные расходы определяют стоимость проекта. С помощью дополнительных ресурсов можно добиться сокращения времени выполнения критических работ. Тогда стоимость этих работ возрастет, но общее время выполнения проекта уменьшится, что может привести к снижению общей стоимости проекта. Предполагается, что работы можно выполнить либо в стандартные, либо в минимальные сроки, но не в промежутке между ними. Пример. Дан сетевой график выполнения некоторых работ в производстве. Необходимо минимизировать общее время выполнения проекта с наименьшими дополнительными затратами.
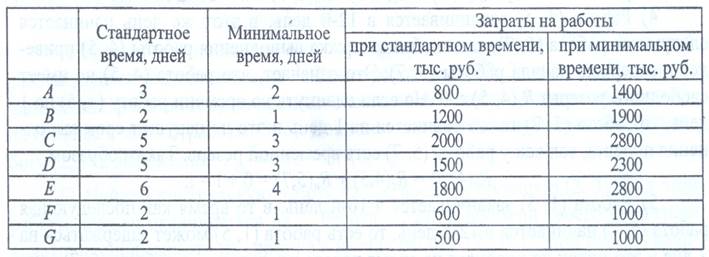
Необходимые исходные данные указаны в таблице.
Решение. Найдем критический путь при условии, что все работы совершаются в минимальное время. Минимальное время, за которое может быть завершен проект - 9 дней. Критический путь А-С-Е. Мы видим, что работы В, D, F, G лежат на критическом пути.
Посмотрим, нельзя ли их выполнить в стандартные сроки без увеличения общего времени выполнения проекта (9 дней). Выполнение этих работ в стандартное время дает следующую экономию: 700 (В), 800 (D), 400 (F), 500 (G). Поэтому порядок рассмотрения будет такой: D, В, G, F. D: мы не можем увеличить продолжительность работы D = (3, 4) с 3 до 5 дней, так как тогда изменится оценка В: увеличение продолжительности работы В = (1,3) с l-го до 2-х дней возможно
Появятся 2 критических пути: A-C-E и B-D-E. Работы А и С мы должны по-прежнему выполнять в минимальное время, иначе изменится критический путь. G: увеличение продолжительности с l-гo дня до 2-х дней возможно.
F: увеличение продолжительности с l-го дня до 2-х дней возможно.
Мы видим, что работы А, С, D, Е выполняются в минимальное время, а работы В, F, G - в стандартное. Общая стоимость проекта составит: 1400(А) + +1200(В) + 2800(С) + 2300(D) + 2800(Е) + 600(F)+ +500(G) = 11600 (тыс. руб.). Использование нелинейной зависимости «затраты - продолжительность» существенно усложняет вычисления. Поэтому иногда нелинейную зависимость можно аппроксимировать кусочно-линейной, когда операция разбивается на части, каждая из которых соответствует одному линейному отрезку. Следует отметить, что наклоны этих отрезков при переходе от точки нормального режима к точке максимально интенсивного режима возрастают. Если это условие не выполняется, то аппроксимация не имеет смысла. Определив зависимость «затраты - продолжительность», для всех операций сети принимают нормальную продолжительность. Далее рассчитывается сумма затрат на все операции сети при этой продолжительности работ. На следующем этапе рассматривается возможность сокращения продолжительности работ. Этого можно достичь за счет уменьшения продолжительности какой-либо критической операции. Только критические операции следует подвергать анализу. Чтобы добиться сокращения продолжительности выполнения работ при минимально возможных затратах, необходимо в максимально допустимой степени сжать ту критическую операцию, у которой наклон кривой «затраты (продолжительность» наименьший. В результате сжатия критической операции получают новый календарный график, возможно, с новым критическим путем. Стоимость работ при новом календарном графике будет выше стоимости предшествующего графика. На следующем этапе этот новый график вновь подвергается сжатию за счет следующей критической операции с минимальным наклоном кривой «затраты - продолжительность» при условии, что продолжительность этой операции не достигла минимального значения. Подобная процедура повторяется, пока все критические операции не будут находиться в режиме максимальной интенсивности. Полученный таким образом оптимальный календарный график соответствует минимуму прямых затрат. Пример. Предприятие решило для улучшения финансового состояния наладить выпуск конкурентоспособной продукции (мороженого). Для переоборудования цеха (участка) под выпуск этой продукции необходимо выполнить: 1) подготовку технического задания на переоборудование участка (30 дней); 2) заказ и поставку нового оборудования (60 дней); 3) заказ и поставку нового электрооборудования (50 дней); 4) демонтаж старого и установку нового оборудования (90 дней); 5) демонтаж старого и установку нового электрооборудования (80 дней); 6) переобучение персонала (30 дней); 7) испытания и сдачу в эксплуатацию оборудования для производства мороженого (20 дней). Ожидается, что производительность после ввода новой линии составит 20 т мороженого в смену. Прибыль от реализации 1 т продукции составит 0,5 тыс. руб. в смену. Деньги на покупку и переоборудование участка в размере 2000 тыс. руб. взяты в банке под 20 % годовых (из расчета 1500 тыс. руб. на закупку оборудования и 500 тыс. руб. на работы по демонтажу старого оборудования и установке нового оборудования). Затраты на проведение работ в нормальном и максимальном режимах указаны в таблице. Улучшить график выполнения работ. С(200, 235), D(300, 1235). Тогда
Решая совместно полученные уравнения, определим время, когда кредит может быть возвращен в банк: Откуда получаем y = 2471, x = 423,6 График выполнения работ может быть сжат за счет достижения на некоторых работах максимально интенсивного режима работы. Вычислим наклоны кривой «затраты - продолжительность» для каждой операции. Наклон определяется как частное от деления прироста стоимости на уменьшение времени выполнения работ. Результаты расчетов приведены в таблице
Учитывая наклоны кривой, производим сжатие операций, имеющих наименьший наклон. Путь (0, 1), (1, 2), (2, 4), (4, 5) может быть сжат до 157 дней, путь (0, 1), (1, 4), (4, 5) - до 72 дней, путь (0, 1), (1, 3), (3,4), (4, 5) - до 157 дней. Дальнейшее сжатие путей (0, 1), (1, 4), (4, 5) и (0, 1), (1, 3), (3, 4), (4, 5) целесообразно, так как стоимостные резервы пути и (0, 1), (1, 2), (2,4), (4, 5) исчерпаны полностью. Этот путь является критическим и дальнейшее уменьшение критического пути не представляется возможным. Таким образом, критический путь сокращен с 200 до 157 дней. Получим сетевой график.
Новый график имеет 2 критических пути: (0, 1), (1, 2), (2, 4), (4, 5) и (0, 1), (1,3), (3, 4), (4, 5). Стоимость сжатия работ составит: (0, 1): 30 тыс. руб. - 20 тыс. руб. = 10 тыс. руб. (1, 2): 60 тыс. руб. - 40 тыс. руб. = 20 тыс. руб. (2, 4): 100 тыс. руб. - 70 тыс. руб. = 30 тыс. руб. (3,4): 70 тыс. руб. - 60 тыс. руб. = 10 тыс. руб. (4,5): 25 тыс. руб. - 20 тыс. руб. = 5 тыс. руб. 10 тыс. руб. + 20 тыс. руб. + 30 тыс. руб. + 10 тыс. руб. + 5 тыс. руб. = 75 тыс. руб. При нормальном режиме работ критический путь составляет 200 дней, стоимость работ - 265 тыс. руб. Критический путь может быть уменьшен до 157 дней, при этом минимальная стоимость работ составит 265 тыс. руб. + 75 тыс. руб. = 340 тыс. руб. График изменения кредита в зависимости от времени остается прежним. Его вид определяет уравнение 10х = 9у -18000. Найдем уравнение прибыли. Через 157 дней после начала работ у предприятия осталось от кредита 2000 -1500 - 265 -75 = 160 тыс. руб. Через 100 дней после начала выпуска продукции предприятие получит прибыль 20 (тыс. руб.) * 0,5 (тыс. руб.) * 100 (дней) = 1000 тыс. руб., и у него будет в наличии 1000 + 160 = 1160 тыс. руб. Таким образом, для нахождения уравнения прибыли предприятия имеем две точки: С'(157, 160) и D'(257, 1160). Согласно уравнению прямой, проходящей через 2 точки, получим
Решая совместно уравнения 10x=9y-1800 и 10x=y+1400, определим время, когда кредит может быть возвращен в банк: 8y-16590=0, y=2426, x=383,6
Работа - это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание), приводящий к достижению намеченного результата.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 984; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.98.39 (0.023 с.) |




 (j) свершения события j называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счет времени ведется от момента наступления начального события. Ранний срок начального события равен 0.
(j) свершения события j называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы. Счет времени ведется от момента наступления начального события. Ранний срок начального события равен 0. 
 (i) - для i -гo события.
(i) - для i -гo события.
 ) - продолжительность максимального пути, проходящего через работу (i, j);
) - продолжительность максимального пути, проходящего через работу (i, j); - продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.
- продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем. = 1.
= 1. (i,j) > 0,8 - напряженные;
(i,j) > 0,8 - напряженные;
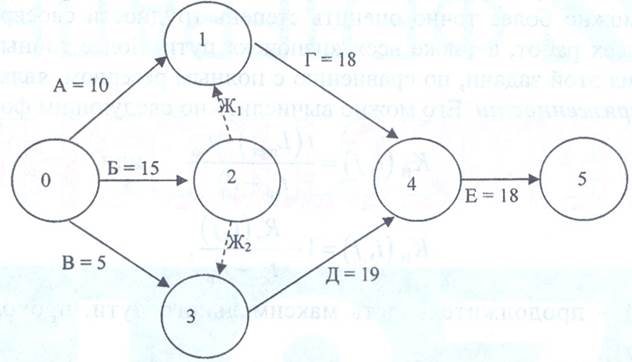
 и
и  введены для устранения параллельности работ Г и Д. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного собьпия и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляет одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.
введены для устранения параллельности работ Г и Д. Расчет критического пути включает два этапа. Первый называется прямым проходом. Вычисления начинают с исходного собьпия и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляет одно число, представляющее ранний срок его наступления. На втором этапе, называемом обратным проходом, вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления.
 (3) - t (1, 3);
(3) - t (1, 3);

 ,=1, 3, 4, 5, 6, длительностью
,=1, 3, 4, 5, 6, длительностью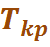 = 52 часа. За выполнением работ этого пути необходим особый контроль, так как любое увеличение их длительности нарушит срок выполнения проекта в целом.
= 52 часа. За выполнением работ этого пути необходим особый контроль, так как любое увеличение их длительности нарушит срок выполнения проекта в целом.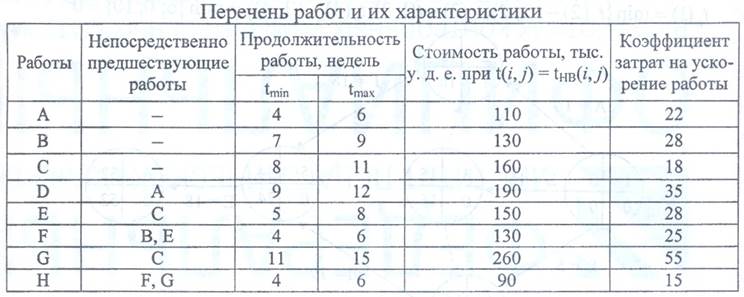
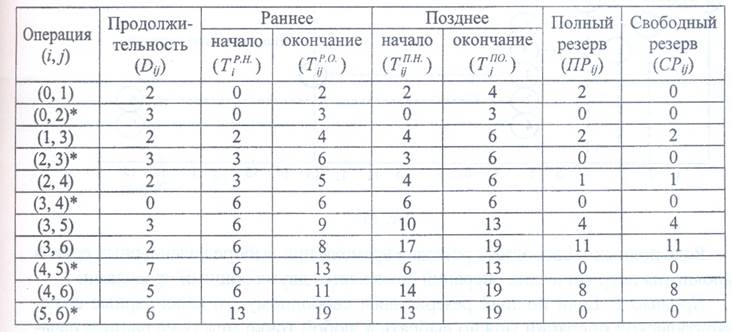

 ). Кроме того, следует учесть, что критический путь является полным, т. е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.
). Кроме того, следует учесть, что критический путь является полным, т. е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.

 (5, 7) =
(5, 7) =  (5, 7).
(5, 7). , предшествующую (6, 7). Код этой работы должен оканчиваться на 6. Таких работ две - (4,6) и (3,6). Но только одна из них - работа (3, 6) - по времени своего окончания вплотную «примыкает» на графике к началу работы
, предшествующую (6, 7). Код этой работы должен оканчиваться на 6. Таких работ две - (4,6) и (3,6). Но только одна из них - работа (3, 6) - по времени своего окончания вплотную «примыкает» на графике к началу работы =... (6, 7)
=... (6, 7)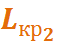 =... (3, 7)
=... (3, 7)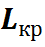 приводит к результату
приводит к результату 
 (4) и изменится критический путь, т. е. общее время выполнения проекта увеличится.
(4) и изменится критический путь, т. е. общее время выполнения проекта увеличится.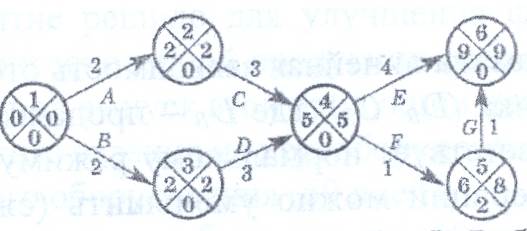




 424 дня.
424 дня.

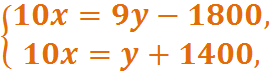
 дня.
дня. 


