Для наглядности выделим на графике привязки критические работы жирной линией.

II. Поиск резервов работ.

Для всех найденных критических работ впишем в таблицу нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца таблицы.

2) Работа (5, 7), согласно графику привязки

(см. рис. 19) заканчивается в 13-й день, а завершающее событие 7 сети, в которое она входит, наступает лишь в 14-й день. То есть, если работа (5, 7) задержится на 1 день, то это не повлияет на срок выполнения проекта ( = 14 дней). Поскольку (5,7) - завершающая работа сети, то ее полный и свободный резервы равны (5, 7) = (5, 7) = 1.

3) Работа (4, 6) заканчивается в 8 -й день, в то время как последующая работа (6, 7) начинается в 10 -й день. То есть работа (4,6) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (6, 7), т. е. (4, 6) = 2.

Полный резерв любой работы складывается из собственного свободного резерва и минимального из полных резервов непосредственно следующих работ.

За работой (4, 6) следует только критическая работа (6, 7) с нулевым полным резервом. Поэтому (4,6) = (4, 6)+ (6, 7) = 2 + 0 = 2.

4) Работа (4, 5) заканчивается в 12 -й день, в этот же день начинается следующая работа (5, 7), т. е. любая задержка выполнения работы (4, 5) приведет к задержке начала работы (5, 7). Это означает, что работа (4, 5) не имеет свободного резерва (4, 5) = 0. Но если сдвинуть во времени работу (4, 5) на 1 день, то работа (5, 7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, так как у работы (5, 7) есть временной резерв. Таким образом,

(4, 5) = (4,5) + (5,7) = 0 + 1 = 1.

5) Работа (1, 5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день, то есть работа (1, 5) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (5, 7), т. е. (l, 5) = 2. Кроме того, поскольку последующая работа (5, 7) имеет резерв в 1 день, то работу (1, 5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис. 19), т. е.

(1, 5) = (1, 5) + (5, 7) = 2 + 1 = 3.

6) Работа (1, 4) заканчивается во 2-й день, и в этот же день начинаются следующие работы (4, 5) и (4, 6), то есть работа (1, 4) не имеет свободного резерва времени, (1, 4) = 0. Поскольку после работы (1, 4) следуют две работы с различными полными резервами, то

(1, 4) = (1, 4) + min[ (4, 5 > (4, 6)] = О + +min[l; 2]=0 + 1 = 1.

7) Работа (1, 3) заканчивается в 3 -й день, а следующие за ней работы (3, 6) и (3, 7) начинаются в 5-й день, т. е. (1, 3) = 2. Поскольку обе последующие рааботы критические, то полный и свободный резерв работы (1, 3) совпадают (l, 3) = (l, 3) + min[ (3, 6); (3,7)] = 2 + min[0; 0] = 2 + 0 = 2.

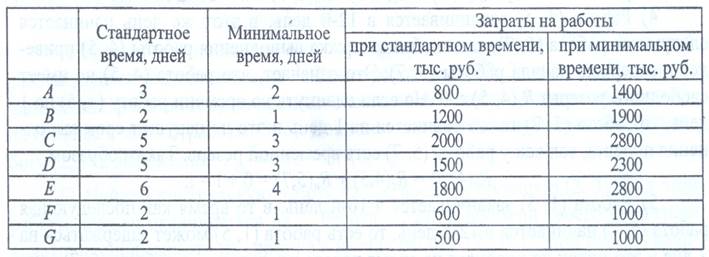
Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками

(см. рис. 19).

Стоимость проекта. Оптимизация сетевой модели 2.3.1. Минимизация общего времени выполнения проекта с наименьшими дополнительными затратами

Стоимость выполнения каждой работы плюс дополнительные расходы определяют стоимость проекта. С помощью дополнительных ресурсов можно добиться сокращения времени выполнения критических работ. Тогда стоимость этих работ возрастет, но общее время выполнения проекта уменьшится, что может привести к снижению общей стоимости проекта. Предполагается, что работы можно выполнить либо в стандартные, либо в минимальные сроки, но не в промежутке между ними.

Пример. Дан сетевой график выполнения некоторых работ в производстве. Необходимо минимизировать общее время выполнения проекта с наименьшими дополнительными затратами.

Необходимые исходные данные указаны в таблице.

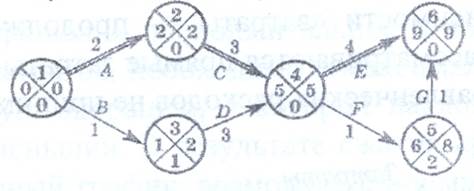
Решение. Найдем критический путь при условии, что все работы совершаются в минимальное время. Минимальное время, за которое может быть завершен проект - 9 дней. Критический путь А-С-Е. Мы видим, что работы В, D, F, G лежат на критическом пути.

Посмотрим, нельзя ли их выполнить в стандартные сроки без увеличения общего времени выполнения проекта (9 дней). Выполнение этих работ в стандартное время дает следующую экономию: 700 (В), 800 (D), 400 (F), 500 (G). Поэтому порядок рассмотрения будет такой: D, В, G, F.

D: мы не можем увеличить продолжительность работы D = (3, 4) с 3 до 5 дней, так как тогда изменится оценка (4) и изменится критический путь, т. е. общее время выполнения проекта увеличится.

В: увеличение продолжительности работы

В = (1,3) с l-го до 2-х дней возможно

Появятся 2 критических пути: A-C-E и B-D-E. Работы А и С мы должны по-прежнему выполнять в минимальное время, иначе изменится критический путь.

G: увеличение продолжительности с l-гo дня до

2-х дней возможно.

F: увеличение продолжительности с l-го дня до

2-х дней возможно.

Мы видим, что работы А, С, D, Е выполняются в минимальное время, а работы В, F, G - в стандартное. Общая стоимость проекта составит: 1400(А) + +1200(В) + 2800(С) + 2300(D) + 2800(Е) + 600(F)+ +500(G) = 11600 (тыс. руб.).