
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изобразить проект с помощью сетевой модели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определить наиболее вероятную продолжительность каждой работы. Найти все полные пути сетевого графика, определить критический путь, ожидаемую продолжительность выполнения проекта и полную стоимость всех работ. Решение. Построим сетевую модель проекта:
Наиболее вероятная продолжительность работ tHB = (2tmin + 3tmax)/5. tНВ А = (2·4 + 3 · 6)/5 = 5,2 tНВ В = (2 · 7 + 3 · 9)/5 = 8,2 tНВ С= (2' 8 + 3 ·11)/5= 9,8 tНВ D= (2· 9 + 3 · 12)/5 = 10,8 tНВ Е = (2 · 5 + 3 · 8)/5 = 6,8 tНВ F= (2·4 + 3 · 6)/5 = 5,2 tНВ G= (2· 11 + 3 · 15)/5 = 13,4 tНВ Н = (2 · 4 + 3 · 6)/5 = 5,2 Возможные полные пути I. 1 - 2 - 5. Длина: tНВ А + tHB D = 5,2 + 10,8 = 16. II. 1 - 3 - 6 - 5. Длина: tНВ В + tHB F+ tHB Н = 8,2 + 5,2 +5,2 = 18,6. III. 1 - 4 - 6 - 5. Длина: tНВ С+ tНВ G+ tHB Н = 9,8 + 13,4 + 5,2,= 28,4. IV. 1 - 4 - 3 - 6 - 5. Длина: tHB C+ tHB В+ tHB P+ tHB H= 9,8 + 6,8 + 5,2 + 5,2 = =27. Максимальная длина пути, равная 28,4 недели, соответствует пути III, на котором лежат работы С, G, Н. Следовательно, он является критическим. Построение календарного графика Пример. Рассмотрим сетевую модель с исходным событием О и завершающим событием 6.
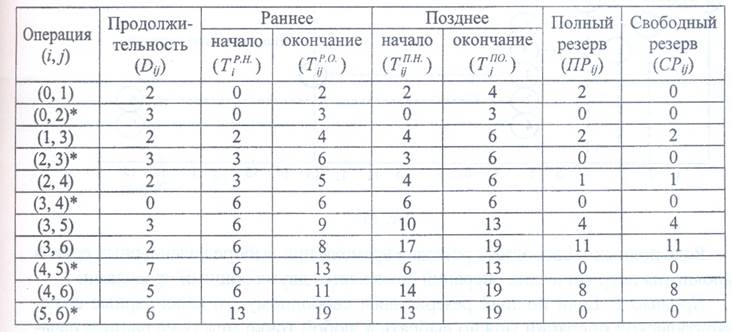
Построить календарный график модели. Решение. Данные, необходимые для построения календарного графика, приведены в таблице. Прежде всего, определяются календарные сроки выполнения критических операций. Далее рассматриваются некритические операции, и указываются их ранние сроки начала (
Критические операции изображаются сплошными линиями. Отрезки времени, в пределах которых могут выполняться некритические операции, наносятся пунктирными линиями, показывающими, что календарные сроки этих операций можно выбрать в указанных пределах при условии сохранения отношений следования. На рисунке 18 показан календарный график, соответствующий примеру. Фиктивная операция (3, 4) не требует затрат времени, поэтому показана на графике вертикальным отрезком. Числа, проставленные над некритическими операциями, соответствуют их продолжительностям.
Роль полных и свободных резервов времени при выборе календарных сроков выполнения некритических операций объясняется двумя общими правилами: Правило 1. Если полный резерв равен свободному, то календарные сроки некритической операции можно выбрать в любой точке между ее ранним началом и поздним окончанием (пунктирные отрезки на рисунке 18). Правило 2. Если свободный резерв меньше полного, то срок начала некритической операции можно сдвинуть по отношению к ее раннему сроку начала не более чем на величину свободного резерва, не влияя при этом на выбор календарных сроков непосредственно следующих операций. В рассматриваемом примере правило 2 применимо только к операции (0, 1), а календарные сроки всех остальных операций выбираются по правилу 1. 2.2.3. График привязки (график Ганта) Для небольших проектов удобным дополнением к сетевому графику является линейный график (график Ганта). Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси - отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа (i, j) может выполняться только после того, как будут выполнены все предшествующие ей работы (k, i). При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта ( Из вышеприведенных соображений следует способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево): 1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие имеет номер завершающего события сети); 2) из всех работ сети (k, i), конечное событие которых i совпадает с начальным событием i работы (i, j), найденной в п. 1, выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j); 3) из всех работ сети (l, k), конечное событие которых k совпадает с начальным событием k работы (k, i), найденной в п. 2, выбрать и выписать ту, которая на графике вплотную примыкает к работе (k, i); 4) продолжать п. 3 до тех пор, пока не будет найдена исходная работа сети, т. е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1). Следует заметить, что если в сетевой модели несколько критических путей, то, выполняя вышеописанные действия, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критических путей. Тем не менее, такой способ хорош для учебных целей, поскольку дает понимание значения критических работ в сетевой модели и учит «читать» и понимать график привязки. Пример. По данным о кодах и длительностях работ в днях построить график привязки сетевой модели, определить критические пути и их длительность. Определить свободные и полные резервы каждой работы, отметить на графике привязки свободные резервы работ.
Решение. I. Поиск критических путей. 1) Построим график привязки (рис. 19).
2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис. 19) две работы (6, 7) и (3, 7), которые заканчиваются позже остальных в завершающем событии № 7. Записываем работы, определенные как критические справа налево. 3) Найдем критическую работу из (6, 7). Допишем слева найденную критическую работу (3, 6) к выражению
4) Найдем критическую работу из 5) Найдем критическую работу из (2, 3). С этой работы начинается критический путь 6) Аналогичный поиск работ критического пути В другой форме записи
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 929; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.201 (0.008 с.) |


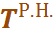 ) и поздние сроки окончания (
) и поздние сроки окончания ( 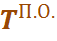 ).
).

 ). Кроме того, следует учесть, что критический путь является полным, т. е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.
). Кроме того, следует учесть, что критический путь является полным, т. е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.

 (5, 7) =
(5, 7) =  (5, 7).
(5, 7). , предшествующую (6, 7). Код этой работы должен оканчиваться на 6. Таких работ две - (4,6) и (3,6). Но только одна из них - работа (3, 6) - по времени своего окончания вплотную «примыкает» на графике к началу работы
, предшествующую (6, 7). Код этой работы должен оканчиваться на 6. Таких работ две - (4,6) и (3,6). Но только одна из них - работа (3, 6) - по времени своего окончания вплотную «примыкает» на графике к началу работы =... (6, 7)
=... (6, 7)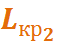 =... (3, 7)
=... (3, 7) приводит к результату
приводит к результату 


