
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие стратегии, оптимальной во множестве смешанных стратегий. Основная теорема матричных игр дж. Фон нейманаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение V=
Полным решением игры в смешанных стратегиях называется совокупность Основная теорема матричных игр фон Неймана. Любая матричная игра имеет решение в смешанных стратегиях, то есть существует цена игры в смешанных стратегиях
Критерий оптимальности смешанной стратегии игрока А в терминах, задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества смешанных стратегий игрока В Теорема (Критерий оптимальных стратегий.) Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, SB– множества смешанных стратегий игрока В. Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы выполнялось нер-во Н(Р0,Q) т.е. выбор игроком А оптимальной стратегии Р0 гарантирует ему выигрыш Н(Р0,Q), не меньший цены игры V, при любой стратегии Q игрока В. Док-во: Необходимость. Пусть Р0- опт стратегия игрока А. тогда по т. Фон Неймана показатель эфф-ти α(Р) стратегии Р0 равен цене игры V: Рассматривая Из равенств (2)-(3)получаем (1) Достаточность. Пусть для некоторой стр-гии Р0 игрока А выполнется нер-во (1) Для док-ва оптимальности стратегии Р0 достаточно показать справедливость равенства: Т.к. нер-во(1) выполняется для любой стратегии Q Но цена игры V равна нижней цене игры Совокуп (5) и (6) эквивалентна рав-ву (4). Достаточность доказана. Теорема доказана.
Критерий оптимальности смешанной стратегии игрока В в терминах задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества смешанных стратегий игрока А Теорема (Критерий оптимальных стратегий.) Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, SA – множества смешанных стратегий игрока А. Для того чтобы стратегияQ0 игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство Н(Р0,Q) т.е. выбор игроком В оптимальной стратегии Q0 гарантирует ему проигрыш Н(Р, Q0), не больший цены игры V, при любой стратегии Р игрока А. Док-во: Необходимость. Пусть Q0- опт стратегия игрока B. тогда по т. Фон Неймана показатель эфф-ти β(Q)стратегии Q0 равен цене игры V: Рассматривая Из равенств (2)-(3)получаем (1) Достаточность. Пусть для некоторой стр-гии Q0 игрока B выполнется нер-во (1) Для док-ва оптимальности стратегии Q0 достаточно показать справедливость равенства: Т.к. нер-во(1) выполняется для любой стр-гии Q Но цена игры V равна верхней цене игры Совокуп (5) и (6) эквивалентна рав-ву (4). Достаточность доказана. Теорема доказана. Критерий оптимальности смешанной стратегии игрока А в терминах, задаваемых цены игры в смешанных стратегиях, выигрыш-функции и множества чистых стратегий игрока В Теорема Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы Н(Р0, Док-во: Достаточно установить эквивалентность нер-в Пусть справедливо нер-во (2). Т.к. это нер-во имеет место для любой стр-гии Q Теперь пусть имеет место быть нер-во (1). Тогда по ф-ле с учетом того, что
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.134.161 (0.007 с.) |

 = v называется ценой игры в смешанных стратегиях, а стратегии
= v называется ценой игры в смешанных стратегиях, а стратегии  и
и  , для которых выполняется равенство
, для которых выполняется равенство  называются оптимальными смешанными стратегиями соответственно игроков А и В. Оптимальные смешанные стратегии
называются оптимальными смешанными стратегиями соответственно игроков А и В. Оптимальные смешанные стратегии 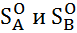 множества оптимальных стратегий игроков А и В. Очевидно, что множество оптимальных стратегий каждого из игроков является подмножеством множества смешанных стратегий:
множества оптимальных стратегий игроков А и В. Очевидно, что множество оптимальных стратегий каждого из игроков является подмножеством множества смешанных стратегий: 
 , то есть цена игры в смешанных стратегиях
, то есть цена игры в смешанных стратегиях  не меньше нижней цены игры в чистых стратегиях α и не больше верхней цены игры в чистых стратегиях β.
не меньше нижней цены игры в чистых стратегиях α и не больше верхней цены игры в чистых стратегиях β. множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий
множеств оптимальных стратегий игроков и цены игры. Любая пара оптимальных стратегий  образуют частное решение в смешанных стратегиях.
образуют частное решение в смешанных стратегиях. v
v  =
= 
 V для любого Q
V для любого Q  SB, (1)
SB, (1) (2)
(2) как пок-ль эф-ти
как пок-ль эф-ти  стратегии Р0 относит множ-ва SB смеш стр-гий игрока В, будем иметь по опр-нию:
стратегии Р0 относит множ-ва SB смеш стр-гий игрока В, будем иметь по опр-нию:  (3)
(3) (4)
(4) (5)
(5) , по опр кот.
, по опр кот.  (6)
(6) V для любого Р
V для любого Р  SA, (1)
SA, (1) (2)
(2) как пок-ль эф-ти
как пок-ль эф-ти  стратегии Q0 относит множ-ва SA смеш стр-гий игрока A, будем иметь по опр-нию:
стратегии Q0 относит множ-ва SA смеш стр-гий игрока A, будем иметь по опр-нию:  (3)
(3) (4)
(4) (5)
(5) , по опр кот.
, по опр кот.  (6)
(6) =
=  – множества чистых стратегий игрока В.
– множества чистых стратегий игрока В. )
)  SB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Вj
SB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Вj  , j=1,…,n, т.е. нер-во (1) имеет место =>
, j=1,…,n, т.е. нер-во (1) имеет место => 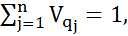 получим
получим Q
Q 


