Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о геометрической интерпретации множества стратегий игрока В, оптимальных во множестве смешанных стратегийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множество Док-во: Для каждой оптимальной стратегии P0=( Множество точек P0=( Так как к тому же множество оптимальных стратегий Это утверждение для множества оптимальных стратегий 35. Критерий в терминах множеств смешанных стратегий игроков А и В того, что число V – цена игры в смешанных стратегиях, а P0, Q0 – стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и В Теорема. Для того, чтобы V было ценой игры, а P0, Q0-оптимальными стратегиями соответственно игроков А и В, другими словами для того, чтобы {P0, Q0, V} было решением игры, необходимо и достаточно выполнение двойного нер-ва
P Доказательство. Необходимость. Пусть V – цена игры и P0, Q0- оптимальные стратегии. Тогда по необходимой части теоремы о критериях оптимальных смешанных стратегий в терминах цены игры, функции выигрышей и множеств смешанных стратегий игроков справедливы нер-ва Н(Р0, Q) Достаточность. Пусть для некоторого числа V и некоторых стратегий P0 игрока А и Q0 игрока В выполняется двойное неравенство (1). Так как это нер-во верно для любых P
Подставим это значение V в (1):
Т.к. неравенство (3) имеет место при любых P Отсюда по определению верхней и нижней цен игры получим: Но по основной теореме матричных игр фон Неймана
Из (2) и (5) следует, что V – цена игры, а также справедливость рав-ва 36. Критерий в терминах множеств чистых стратегий игроков А и В того, что число V – цена игры в смешанных стратегиях, а Р0 и Q0 – стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и В Пусть Для того, чтобы V была ценой игры, Р0 и Q0- оптимальными стратегиями игроков А и В, необходимо и достаточно выполнение двойного нер-ва Док-во: пусть справедливо нер-во
P
37. Критерий в терминах седловых точек выигрыш-функции того, что число V – цена игры в смешанных стратегиях, а Р0 и Q0 – стратегии, оптимальные во множестве смешанных стратегий соответственно игроков А и В
Для того, чтобы V была ценой игры, а 𝑃0, 𝑄0 – оптимальными стратегиями соответственно игроков А и В, необходимо и достаточно, чтобы (𝑃0, 𝑄0) была седловой точкой функции выигрыша 𝐻(𝑃,𝑄) и 𝐻(𝑃0, 𝑄0)=𝑉 Доказательство: 1) Необходимость. Пусть V – цена игры и 𝑃0, 𝑄0 – оптимальные стратегии. Следовательно, по необходимой части критерия цены игры и оптимальных смешанных стратегий игроков в терминах множеств смешанных стратегий выполняется неравенство 𝐻(𝑃, 𝑄0)≤𝑉≤𝐻(𝑃0,𝑄) Но тогда имеет место неравенство 𝐻(𝑃,𝑄0)≤𝐻(𝑃0,𝑄0)≤𝐻(𝑃0,𝑄), 𝑃𝜖𝑆𝐴 и 𝑄𝜖𝑆𝐵, которое означает, что (𝑃0, 𝑄0) – седловая точка функции выигрыша 𝐻(𝑃,𝑄) (по определению седловой точки). Так как V – цена игры и 𝑃0, 𝑄0 – оптимальные стратегии, то равенство 𝐻(𝑃0, 𝑄0)=𝑉 выполняется по определению. 2) Достаточность. Пусть (𝑃0, 𝑄0) – седловая точка функции выигрыша 𝐻(𝑃,𝑄) и имеет место равенство 𝐻(𝑃0, 𝑄0)=𝑉. По определению седловой точки справедливо неравенство 𝐻(𝑃, 𝑄0)≤𝐻(𝑃0, 𝑄0)≤𝐻(𝑃0,𝑄), 𝑃𝜖𝑆𝐴 и 𝑄𝜖𝑆𝐵. То есть 𝐻(𝑃, 𝑄0)≤𝑉≤𝐻(𝑃0,𝑄), 𝑃𝜖𝑆𝐴 и 𝑄𝜖𝑆𝐵. Отсюда по достаточной части критерия цены игры и оптимальных смешанных стратегий игроков в терминах множеств смешанных стратегий вытекает, что V – цена игры и 𝑃0, 𝑄0 – оптимальные стратегии игроков А и В. Определения активных и пассивных чистых стратегий и теорема об активных стратегиях Пусть 𝑃0=(𝑝10,…,𝑝m0) – оптимальная смешанная стратегия игрока А. В общем случае, некоторые из вероятностей 𝑝10,…,𝑝m0 могут быть равными нулю. Если 𝑝i0=0, где i – одно из чисел 1,…,m, то в оптимальной смешанной стратегии 𝑃0=(𝑝10,…,𝑝m0) чистая стратегия 𝐴𝑖 не участвует и потому называется пассивной. Чистые стратегии 𝐴𝑖, входящие в оптимальную стратегию 𝑃0 с положительной вероятностью 𝑝i0>0, называются активными стратегиями игрока А. Аналогично определяются активные стратегии игрока В. Теорема (об активных стратегиях). Пусть V – цена игры и 𝑃0=(𝑝10,…,𝑝m0), 𝑄0=(𝑞10,…,𝑞n0) - оптимальные стратегии соответственно игроков А и В. Тогда справедливы следующие утверждения. 1. Для любой активной стратегии 𝐴k,(𝑘𝜖{1,…,𝑚}) игрока А выполняется равенство 𝐻(𝐴k,𝑄0)=𝑉 2. Для любой активной стратегии 𝐵l (𝑙𝜖{1,…,𝑛}) игрока В выполняется равенство 𝐻(𝑃0,𝐵l)=𝑉
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.006 с.) |

 оптимальных стратегий игрока B является выпуклым многогранником (политопом), содержащимся в симплексе SB всех смешанных стратегий игрока B.
оптимальных стратегий игрока B является выпуклым многогранником (политопом), содержащимся в симплексе SB всех смешанных стратегий игрока B.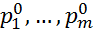 ) игрока A из теоремы об оптимальности смешанных стратегий игрока А справедливо неравенство Н(Р0,
) игрока A из теоремы об оптимальности смешанных стратегий игрока А справедливо неравенство Н(Р0,  )
)  V, j=1,…,n.
V, j=1,…,n.  . Тогда
. Тогда 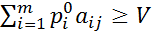 , j=1,…,n.
, j=1,…,n. i=1,…,m, которых удовлетворяют этому неравенству для фиксированного j
i=1,…,m, которых удовлетворяют этому неравенству для фиксированного j  {1,…,n}, является замкнутым полупространством, а множество точек P0=(
{1,…,n}, является замкнутым полупространством, а множество точек P0=( игрока A ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то
игрока A ограничено, поскольку оно является подмножеством симплекса всех его смешанных стратегий SA, то  игрока В доказывается аналогично.
игрока В доказывается аналогично. для любых
для любых SA и Q
SA и Q  SB (1)
SB (1) V для любого Q
V для любого Q  V для любого Р
V для любого Р  SA, их можно записать в виде двойного нер-ва
SA, их можно записать в виде двойного нер-ва  для любых P
для любых P  , т.е.
, т.е.  (2)
(2) , P
, P 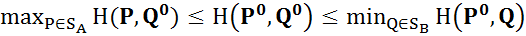 ó
ó 
 (4)
(4) и из (4) получим получим рав-ва:
и из (4) получим получим рав-ва: (5)
(5) , кот. по определению оптимальных стратегий, означает, что
, кот. по определению оптимальных стратегий, означает, что  и
и  –оптимальные стратегии соответственно игроков А и В.
–оптимальные стратегии соответственно игроков А и В. =
=  и
и  =
=  – множества чистых стратегий игроков А и В.
– множества чистых стратегий игроков А и В.
 и равенства
и равенства  получим
получим