Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование дробно-рациональных функцийСодержание книги
Поиск на нашем сайте
146. Задание {{ 205 }} Дробно-рациональные интегралы Отметьте правильный ответ Пусть задана функция
£ £ R £ 147. Задание {{ 206 }} Дробно-рациональные Отметьте правильный ответ Пусть задана функция
£ R £ £ 148. Задание {{ 207 }} Дробно-рациональные Отметьте правильный ответ Пусть задана функция
£ R £ £ 149. Задание {{ 208 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
R £ £ £ 150. Задание {{ 209 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
£ £ R £ 151. Задание {{ 210 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
£ £ R £ 152. Задание {{ 211 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
£ £ £ R 153. Задание {{ 212 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
R £ £ £ 154. Задание {{ 213 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
£ £ R £ 155. Задание {{ 214 }} Дробно-рациональные Отметьте правильный ответ Неопределенный интеграл
R £ £ £ Интегрирование по частям 156. Задание {{ 100 }} Интегрирование по частям опред Отметьте правильный ответ Метод интегрирования, суть которого определяется формулой
£ интегрирования подстановкой
£ непосредственного интегрирования
R интегрирования по частям
£ замены переменной интегрирования
157. Задание {{ 160 }} Интегрирование по частям Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
R
£
£
£
158. Задание {{ 161 }} Интегрирование по частям Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
R
£
£
159. Задание {{ 162 }} Интегрирование по частям пример Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
£
£
R
160. Задание {{ 164 }} Интегрирование по частям Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
£
£
R
161. Задание {{ 165 }} Интегрирование по частям Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
R
£
£
£
162. Задание {{ 166 }} Интегрирование по частям пример Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
R
£
£
163. Задание {{ 167 }} Интегрирование по частям пример Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
£
R
£
164. Задание {{ 168 }} Интегрирование по частям Отметьте правильный ответ Интегрируя по частям можно показать, что интеграл
£
£
£
R
165. Задание {{ 187 }} Интегрирование по частям 1 Отметьте правильный ответ Неопределенный интеграл
£ R £ £ 166. Задание {{ 188 }} Интегрирование по частям1 Отметьте правильный ответ Неопределенный интеграл
£ £ £ R 167. Задание {{ 189 }} Интегрирование по частям 1 Отметьте правильный ответ Неопределенный интеграл
£ £ R £ 168. Задание {{ 190 }} Интегрирование по частям 1 Отметьте правильный ответ Неопределенный интеграл
R £ £ £ 169. Задание {{ 191 }} Интегрирование по частям 1 Отметьте правильный ответ Неопределенный интеграл
R £ £ £ 170. Задание {{ 192 }} Интегрирование по частям 1 Отметьте правильный ответ Неопределенный интеграл
£ R £ £ 171. Задание {{ 193 }} Интегрирование по частям Отметьте правильный ответ Неопределенный интеграл
R £ £ £ 172. Задание {{ 194 }} Интегрирование по частям1 Отметьте правильный ответ Неопределенный интеграл
£ R £ £
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.180.149 (0.007 с.) |

 . Тогда ее первообразная будет иметь вид:
. Тогда ее первообразная будет иметь вид:



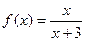 . Тогда ее первообразная будет иметь вид:
. Тогда ее первообразная будет иметь вид:



 . Тогда ее первообразная будет иметь вид:
. Тогда ее первообразная будет иметь вид:



 равен
равен



 равен
равен



 равен
равен

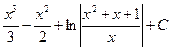

 равен
равен


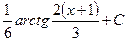
 равен
равен

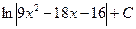
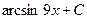
 равен
равен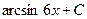



 равен
равен

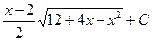

 , называется методом
, называется методом равен
равен

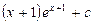

 равен
равен

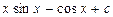

 равен
равен



 равен
равен
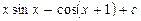
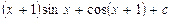

 равен
равен



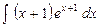 равен
равен
 равен
равен

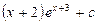
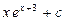
 равен
равен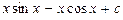



 равен
равен



 равен
равен

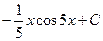

 равен
равен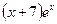



 равен
равен

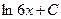

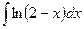 равен
равен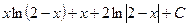


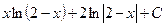
 равен
равен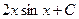



 равен
равен



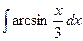 равен
равен