Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл от неотрицательной функции численно равенСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
£ объему тела вращения
R площади криволинейной трапеции
£ длине дуги плоской кривой
£ площади поверхности вращения
287. Задание {{ 260 }} Определение Отметьте правильный ответ Символ
£ неопределенный интеграл
£ ограниченный интеграл;
R определенный интеграл
£ Несобственный интеграл
288. Задание {{ 261 }} Определение Отметьте правильный ответ Числа а и b в выражении
£ параметрами интегрирования
£ символами интегрирования
R пределами интегрирования
289. Задание {{ 262 }} Определение Отметьте правильный ответ Определенный интеграл
£ единице;
R нулю
£ бесконечности.
290. Задание {{ 263 }} Определение Отметьте правильный ответ При перестановке пределов интегрирования определенный интеграл
R меняет знак
£ обращается в нуль
£ стремится к бесконечности
291. Задание {{ 264 }} Определение Отметьте правильный ответ Определённым интегралом от функции
£ число элементарных отрезков неограниченно уменьшается, а длина наибольшего из них стремится к нулю
£ число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к бесконечности
R число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю;
£ число элементарных отрезков неограниченно уменьшается, а длина наибольшего из них стремится к бесконечности
292. Задание {{ 265 }} Определенный теория Отметьте правильный ответ Величина определённого интеграла:
R не зависит от обозначения переменной интегрирования
£ меняет свой знак на противоположный при переобозначении переменной интегрирования
293. Задание {{ 266 }} Определенный интеграл теория Отметьте правильный ответ Определённый интеграл от функции
R отрезкам оси OX;
£ графиком функции
£ отрезком оси OY.
294. Задание {{ 267 }} Определенный интеграл теория Отметьте правильный ответ Определённым интегралом от функции
£ число элементарных отрезков неограниченно уменьшается, а длина наибольшего из них стремится к нулю
£ число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к бесконечности
R число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю;
£ число элементарных отрезков неограниченно уменьшается, а длина наибольшего из них стремится к бесконечно
295. Задание {{ 268 }} Определенный интеграл теория Отметьте правильный ответ Пусть каждая из функций
£
R
£
£
Рейтинговая точка №3 Несобственный интеграл
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 обозначает
обозначает (
( ) равен
) равен на интервале
на интервале  , называется конечный предел ее интегральной суммы, когда
, называется конечный предел ее интегральной суммы, когда на отрезке
на отрезке 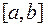 равен площади криволинейной трапеции, ограниченной сверху графиком функции
равен площади криволинейной трапеции, ограниченной сверху графиком функции  , а снизу
, а снизу ;
; и
и  интегрируема на сегменте
интегрируема на сегменте  , удовлетворяющее неравенствам
, удовлетворяющее неравенствам  и такое, что справедлива формула
и такое, что справедлива формула