
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поверхности уровня и линии уровня в скалярном поле. Производная по направлению и градиентСодержание книги
Поиск на нашем сайте Литература. [1], гл. VIII, § 13, 14, 15, упр. 40-43.
Пример. Для функции 1) 2) производную по направлению Решение. Градиент и производная по направлению находятся по формулам:
Координаты единичного вектора Значения частных производных по
В точке А (1;2) частные производные принимают значения
Ответ: Формула Тейлора функции двух переменных. Экстремумы функции нескольких переменных. Литература. [1], гл. VIII, § 16, 17, 19. упр. 47-49. При исследовании функции двух переменных на экстремум обратите внимание на следующее: 1. Точки экстремума всегда лежат внутри области определения, а на границе могут находиться только наибольшие и наименьшие значения (см. функцию одной переменной) 2. Экстремум может достигаться в тех точках области определения, где Пример 1.
График функции z – верхняя половинка конуса. В точке (0;0) производные по x и y не существуют, но
Рис. 4.
Схема исследования на нахождение наибольших и наименьших значений 1. Найти внутренние точки области, где может быть экстремум. 2. Исследовать границы области и найти там точки, где может достигаться наибольшее и наименьшее значения. 3. Вычислить значение функции во всех найденных в п.1 и 2 точках. Среди них выбрать наибольшее и наименьшее. Покажем, как это делается. Пример 2. Найти наибольшее и наименьшее значения функции
Решение. Точки, в которых функция принимает наибольшее и наименьшее значения, могут находиться как внутри области, так и на ее границе. Если функция принимает наибольшее (наименьшее) значение во внутренней точке области, то в этой точке частные производные
найдем две точки О (0; 0) и М (1; 1), в которых обе частные производные равны нулю. Первая из них принадлежит границе области. Следовательно, если функция z принимает наибольшее (наименьшее) значение во внутренней точке области, то это может быть только в точке М(1;1). Перейдем к исследованию функции на границе области. На отрезке ОА имеем
есть возрастающая функция от одной переменной
представляет собой функцию одной переменной Находим производную: На дуге ОВ параболы
Решаем уравнение Следовательно, наибольшее и наименьшее значения функции
Наибольшее и наименьшее из них равны 12 и -1. Они и являются наибольшим и наименьшим значениями данной функции в данной замкнутой области:
Контрольная работа № 3. Задания.
1. Найти неопределенные и определенный интегралы. В двух первых примерах (п. а) и б) проверить результаты дифференцированием.
2. Геометрические приложения определенного интеграла 2.1. Вычислить площадь фигуры, ограниченной параболой 2.2. Вычислить площадь фигуры, ограниченной параболой 2.3. Вычислить площадь фигуры, ограниченной параболой 2.4. Вычислить площадь фигуры, ограниченной параболой 2.5. Вычислить площадь фигуры, ограниченной графиком функции 2.6. Вычислить площадь фигуры, ограниченной графиком функции 2.7. Вычислить площадь фигуры, ограниченной графиком функции 2.8. Вычислить площадь фигуры, ограниченной графиком функции 2.9. Вычислить площадь фигуры, ограниченной графиком функции 2.10. Вычислить площадь фигуры, ограниченной линиями 2.11. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами 2.12. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной полуэллипсом 2.13. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной гиперболой 2.14. Вычислить объем тела, полученного вращением вокруг оси О 2.15. Вычислить объем тела, полученного вращением вокруг оси О 2.16. Вычислить объем тела, полученного вращением вокруг оси О 2.17. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами 2.18. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной полуэллипсом 2.19. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной гиперболой 2.20. Вычислить объем тела, полученного вращением вокруг оси О 3. Дана функция двух переменных 1. Найти область определения функции двух переменных 2. Найти градиент функции в точке А. 3. Проверить, удовлетворяет ли функция двух переменных
4. Найти наименьшее и наибольшее значения функции
Контрольная работа № 4 ЛИТЕРАТУРА
[2]. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Наука, 2006.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 в точке А (1;2) найти
в точке А (1;2) найти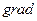
 ;
; .
. ,
, где
где  - единичный вектор направления
- единичный вектор направления 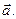
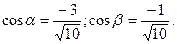
 и по
и по  находим, рассматривая функцию двух аргументов
находим, рассматривая функцию двух аргументов 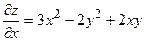 ,
, .
. и, следовательно,
и, следовательно,


 и
и  или равны 0 или не существуют.
или равны 0 или не существуют. ,
,
 ,
,  .
.

 в замкнутой области, ограниченной осью О y, прямой y =2 и параболой
в замкнутой области, ограниченной осью О y, прямой y =2 и параболой 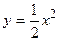 при
при 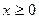 .
. равны нулю. Решив систему уравнений
равны нулю. Решив систему уравнений
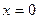 , поэтому на этом отрезке
, поэтому на этом отрезке
 , поэтому на этом отрезке функция
, поэтому на этом отрезке функция
 Решаем уравнение
Решаем уравнение 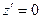 или
или  и находим
и находим 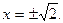 Внутри отрезка
Внутри отрезка 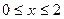 имеется лишь одна критическая точка
имеется лишь одна критическая точка  соответствующей точкой отрезка АВ является точка Q
соответствующей точкой отрезка АВ является точка Q  . Итак, из всех значений функции
. Итак, из всех значений функции 
 .
. или
или  и находим его корни:
и находим его корни: 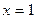 . Таким образом, из всех значений функции
. Таким образом, из всех значений функции  в данной замкнутой области находятся среди ее значений в точках О, А, Q, В, Р, М, т.е. среди значений:
в данной замкнутой области находятся среди ее значений в точках О, А, Q, В, Р, М, т.е. среди значений: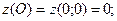

 Q
Q 













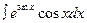

















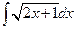

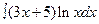

































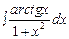










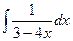


 и прямой
и прямой 
 и прямой
и прямой 
 и прямой
и прямой 
 и прямой
и прямой 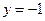 .
. ,
,  и прямой
и прямой  .
. .
. ,
,  и прямой
и прямой  , осью ОХ и прямыми
, осью ОХ и прямыми  .
.

 и
и 
 .
. и прямыми
и прямыми 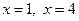 .
. и кубической параболой
и кубической параболой 
 и
и  .
. и
и 
 .
. и прямыми
и прямыми  .
. и кубической параболой
и кубической параболой 
 Изобразить ее на координатной плоскости XOY и заштриховать.
Изобразить ее на координатной плоскости XOY и заштриховать. указанному дифференциальному уравнению первого порядка.
указанному дифференциальному уравнению первого порядка. А(1,2)
А(1,2)


 . А(1,3)
. А(1,3)
 ,
,  , А(0,5;0,5)
, А(0,5;0,5)
 ,
, 
 , А(2,2)
, А(2,2)
 ,
, 
 А(1,1)
А(1,1)
 ,
, 
 А(4,4)
А(4,4)
 ,
, 
 А(1,4)
А(1,4)


 А(1,3)
А(1,3)
 ,
,  А(2,3)
А(2,3)

 А(2,2)
А(2,2)
 ,
, 
 А(2,4)
А(2,4)
 ,
, 
 А(2,2)
А(2,2)
 ,
,  . А(3,2)
. А(3,2)
 ,
, 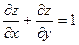
 А(1,3)
А(1,3)
 ,
,  А(2,2)
А(2,2)
 ,
,  А(5,2)
А(5,2)
 ,
, 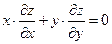
 А(1,4)
А(1,4)
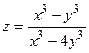 ,
,  А(2,2)
А(2,2)
 ,
,  А(1,1)
А(1,1)
 ,
,  А(2,3)
А(2,3)
 ,
, 
 в замкнутой области D, заданной системой неравенств. Сделать чертеж.
в замкнутой области D, заданной системой неравенств. Сделать чертеж. ;
;




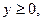













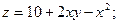











 .
.

 .
.

 .
.

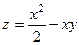
 .
.

 .
.

 .
.

 .
.

 .
.



