
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Номер студенческого билета (или зачетной книжки).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Название дисциплины и номер контрольной работы. Номер варианта.
Номер варианта, который должен выполнять студент, соответствует последней цифре номера студенческого билета (или зачетной книжки). В каждом задании 20 вариантов примеров. Если год Вашего поступления в Университет – чётный, то Вы выбираете пример из первых десяти вариантов, а если – нечётный, то выбираете свой вариант из номеров с одиннадцатого по двадцатый. Например, год поступления 2013, вариант 3, следовательно должны быть выбраны примеры 1.13, 2.13 и т.д. Например, год поступления 2014, вариант 3, следовательно должны быть выбраны примеры 1.03, 2.03 и т.д.
Контрольная работа № 3.
ЛИТЕРАТУРА [1]. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т.1 - М.: Наука, 2002, 2005. Неопределенный интеграл Определение и свойства неопределенного интеграла Литература. [1], гл. Х, §1-3, упр. 2, 5, 7, 9, 11, 14, 16, 17, 25, 41, 46, 49, 58, 60, 66.
Основные методы интегрирования Литература. [1], гл. Х, §4, упр. 27, 28, 33, 37, 47, 51, 65, 72, 83, 89, 91, 94, 100, 101; §6, упр. 127-131, 134, 135, 138, 140, 143, 145.
Пример 1. Решение. Используем теорему: интеграл от разности функций равен разности интегралов.
Пример 2. Вычислить Решение. Сравним наш интеграл стабличным
У нас если В интеграле
. Проверим полученный результат дифференцированием
Интеграл взят правильно.
Пример 3. Решение. Так как
У нас
Пример 4. Решение. Так как
Проверим дифференцированием
Пример 5. Найти Решение. Так как Подставляя в исходный интеграл, имеем Пример 6. Найти Решение. Здесь уместна замена t = cos x, т.к. dt = - sin x dx, и sin3x dx = sin2x sinx dx. Поэтому
Пример 7. Найти Решение. Используем метод интегрирования по частям
Так как производная от х равна 1, то возьмем u = x. Используем формулу, приведя схему записи удобную при использовании метода интегрирования по частям.
Пример 8. Найти Используем метод разложения на простейшие. Знаменатель имеет два различных действительных корня, разложим подинтегральную функцию на простейшие слагаемые
Приравняем числители и учтем, что коэффициенты при одинаковых степенях х, стоящие слева и справа должны совпадать
Следовательно
Определенный интеграл Определение, свойства и вычисление определенного интеграла Литература. [1], гл.XI, § 1-5, 6 (пример можно пропустить), упр. 8, 10, 11, 13, 16-21, 23, 24.
Пример. Вычислить Так как интеграл от суммы функций равен сумме интегралов, то
Геометрические приложения определенного интеграла Литература. [1], гл.XII, §1, упр. 1, 3, 5-11; §2, упр. 13, 14, 17, 18; §3, упр. 38-41, 43, 47; §4, 5, упр. 20-23, 25, 32; §6, упр. 49, 51, 53, 56. Пример 1. Вычислить площадь фигуры, ограниченной линиями Решение. Построим в системе координат
Рис.1. Обозначим эти точки через A и В. Итак, А(1; 5), В(5; 1). Искомая площадь S равна разности площадей фигур, ограниченных линиями S = S1 – S2 Площадь S2 может быть вычислена с применением определенного интеграла
Площадь S1 можно, конечно, вычислить как сумму площадей прямоугольного треугольника и прямоугольника, но удобнее все-таки вычислить S1 как интеграл
Теперь можно вычислить и искомую площадь
S = S1 – S2 = 12 – 5 ln5
Ответ: S =12 – 5 ln5 ед 2. Пример 2. Вычислить объем тела, полученного вращением вокруг оси О Найдем точки пересечения линий. Для этого решим уравнение
Рис. 2.
Объем тела может быть вычислен по формуле
Ответ:
Т е м а 3. Функции нескольких переменных Основные понятия. Литература. [1], гл.VШ, § 1 - 4.
Частные производные. Литература. [1], гл. VIII, § 5, 6, упр. 1-10. Пример. 1. Найти область определения функции. 2. Проверить, что 3. Проверить, что
Решение. 1.Под знаком логарифма может стоять только положительное выражение, следовательно
Сделаем чертеж
Рис. 3.
2. При вычислении частной производной по
3. При вычислении второй производной по
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 765; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.215.54 (0.01 с.) |

 .
.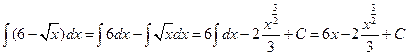
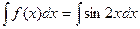 .
.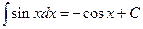
 , формально интеграл не табличный. Используем теорему о линейной замене переменной:
, формально интеграл не табличный. Используем теорему о линейной замене переменной: , то
, то  .
. , т.е. а = 2, следовательно
, т.е. а = 2, следовательно

 , т.е.
, т.е.  .
. , то используем теорему о «замене типа подведение под знак дифференциала»
, то используем теорему о «замене типа подведение под знак дифференциала» , где t = g (x)
, где t = g (x)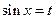 . Тогда
. Тогда 

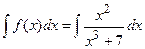 , т.е.
, т.е.  .
. , то то используем теорему о «замене типа подведение под знак дифференциала»,
, то то используем теорему о «замене типа подведение под знак дифференциала»,  . Тогда
. Тогда  . Домножим в числителе на 3, при этом надо и знаменатель умножить на 3.
. Домножим в числителе на 3, при этом надо и знаменатель умножить на 3. .
. .
. .
. , то используем теорему о «замене типа подведение под знак дифференциала» argtgx = t, тогда dt = d(arctg(x)) =
, то используем теорему о «замене типа подведение под знак дифференциала» argtgx = t, тогда dt = d(arctg(x)) =  и earctg x = et
и earctg x = et earctg x + C.
earctg x + C. .
.
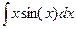 .
.

 = - x cosx +
= - x cosx +  = - x cosx + sinx + C.
= - x cosx + sinx + C. .
.



 .
.
 и
и  .
.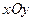 эти линии. Найдем точки пересечения этих линий
эти линии. Найдем точки пересечения этих линий


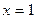 ,
,  ,
,  ,
,  (обозначим эту площадь через S1) и линиями
(обозначим эту площадь через S1) и линиями 
 ед 2.
ед 2. .
. фигуры, ограниченной прямой
фигуры, ограниченной прямой  и параболой
и параболой  .
. . Получим
. Получим  .
.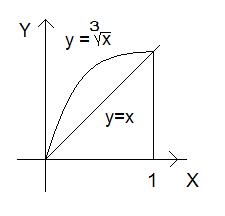
 , где
, где ,
,  .
. .
. .
.



 или
или  .
.
 как функцию только от переменной
как функцию только от переменной  а при дифференцировании по
а при дифференцировании по  - как функцию только от
- как функцию только от  ,
, ,
,
 ,
, ,
,



