
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл второй производнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Физический смысл производной второго порядка проясняется из того, что если первая производная f’(x) задаёт мгновенную скорость изменения значений f(x) в момент времени x в момент времени f’(x), задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений f(x). Следовательно, третья производная - это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения,
14) дифференциал функции Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства:
Линейную функцию
Приближенное значение функции вблизи точки
Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изм 15) признания возрастания и убывания функции Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:
если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X; если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X. Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
решить неравенства к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна. Рассмотрим пример для разъяснения алгоритма. 16) Экстре́мум функции (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум). исследование функции на экстремум При изучении явлений природы и общества мы постоянно имеем дело с изменяемостью различных величин (движение тела, наращивание растительной массы, финансовые потоки и др.), а также с зависимостью одних величин от других. Поэтому одним из основных понятий в математике является понятие о переменной величине, которой является любая величина, принимающая хотя бы два различных значения. Закон, согласно которому одной переменной приведено в соответствие значение другой переменной называется функцией. Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Каждая область знаний: физика, химия, биология, социология, лингвистика и т. д. – имеет свои объекты изучения, устанавливает свойства, и, что особенно важно, взаимосвязи этих объектов. 17)выпуклости графика функции точки перегиба График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый. Доказательство. Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение 18) нахождение наибольшего и наименьшего значения функции с помощью производной Говорят, что функция 19) Первообра́зной [1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием. Так, например, функция Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
Это соотношение называется формулой Ньютона — Лейбница. Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G (x) = F (x) + C для всех x. Число C называют постоянной интегрирования. Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
20) вычисление неопределенным интегралов непосредственно и подстановкой Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием. Примеры.
21) Пусть функция Пусть функция
Пусть интегрируемые на отрезке
Геометрический смысл Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
Рассмотрим график функции y = f (x):
22) вычисление определенного интеграла непосредственно методом подстановки Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница: Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.
Пусть F (x) – первообразная для f (x). Для f (t) первообразной служит та же функция F (t), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
и
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если
то
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции
можно почленно интегрировать, т.е.
23 П ереходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу – как с помощью определенного интеграла вычислить площадь плоской фигуры. Наконец-то ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.
Для успешного освоения материала, необходимо: 1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Неопределенный интеграл. Примеры решений. 2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на странице Определенный интеграл. Примеры решений. Определение вектора
Равенство двух векторов
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.62.14 (0.01 с.) |

 .
. где α – бесконечно малая в окрестности
где α – бесконечно малая в окрестности  функция. Для приближенного вычисления значения функции f в точке x 0 + Δ x эту бесконечно малую функцию можно отбросить:
функция. Для приближенного вычисления значения функции f в точке x 0 + Δ x эту бесконечно малую функцию можно отбросить:
 называют дифференциалом функции f в точке
называют дифференциалом функции f в точке 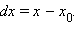 Поэтому пишут:
Поэтому пишут: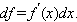

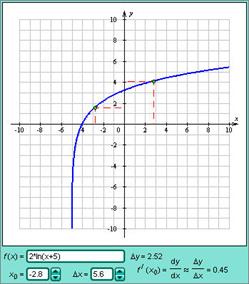
 и
и  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции. выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции. и
и 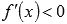 на области определения;
на области определения; . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
. Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство
, определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство  . Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений. Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.
. Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений. Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума. является первообразной
является первообразной  . Так как производная константы равна нулю,
. Так как производная константы равна нулю,  будет иметь бесконечное количество первообразных; таких как
будет иметь бесконечное количество первообразных; таких как  или
или  … и т. д.; таким образом семейство первообразных функции
… и т. д.; таким образом семейство первообразных функции  , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.
, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.


 с
с 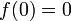 не непрерывна при
не непрерывна при  , но имеет первообразную
, но имеет первообразную  с
с  .
.

 монотонна на отрезке
монотонна на отрезке  , то есть либо не убывает, либо не возрастает на нём. Тогда
, то есть либо не убывает, либо не возрастает на нём. Тогда  . Иными словами, если функция интегрируема, то она ограничена.
. Иными словами, если функция интегрируема, то она ограничена. таковы, что
таковы, что  при всех
при всех  . Тогда
. Тогда



 (40)
(40)


 (41)
(41) (42)
(42)
 (43)
(43) (44)
(44) внутри его, т.е.
внутри его, т.е. (45)
(45)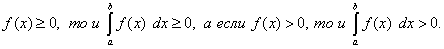
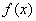 и
и  непрерывны, то неравенство
непрерывны, то неравенство
 (46)
(46) вектор AB, понимая под этим направленный отрезок AB, т. е. отрезок, у которого точка A является началом, а точка B -- концом.
Таким образом, точки A и B, ограничивающие вектор
вектор AB, понимая под этим направленный отрезок AB, т. е. отрезок, у которого точка A является началом, а точка B -- концом.
Таким образом, точки A и B, ограничивающие вектор  одинаковой длины и противоположно направленные.
одинаковой длины и противоположно направленные.
 , расположенные на одной прямой, считаются равными, если равны отрезки AB и CD, т. е. равны длины этих векторов, а лучи AB и CD задают одинаковые направления.
Если же векторы
, расположенные на одной прямой, считаются равными, если равны отрезки AB и CD, т. е. равны длины этих векторов, а лучи AB и CD задают одинаковые направления.
Если же векторы 


