
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объем шара, ограниченного сферойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Площадь сегмента сферы
Сфера в трёхмерном пространстве Уравнение
где Параметрическое уравнение сферы с центром в точке
где 29) Аксиомы стереометрии и их следствия Аксиомы стереометрии и их следствия
30)взаимное расположение двух прямых Взаимное расположение двух прямых на плоскости. Этот вопрос уже обсуждался в предыдущей лекции, когда обауравнения данных прямых записывались в каноническом или параметрическом виде. Пусть сейчас оба уравнения прямых записаны в общем виде. Теорема. Пусть
– общие уравнения двух прямых на координатной плоскости Оху. Тогда 1) если 2) если параллельные; 3) если Доказательство. Условие
Если же
Если же прямые не совпадают и не пересекаются, то остается случай Теорема доказана. Заметим, что если прямые пересекаются, то для нахождения координатих точки пересечения достаточно решить систему двух уравнений сдвумя неизвестными:
Следствие. Пусть
где Если Доказательство. По определению определителя второго порядка
Если Если же следствие доказано. 31)параллельность прямых и плоскостей Определение 2.3. Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая a параллельна плоскости α, то пишут a || α.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости. Доказательство
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a. Доказательство
Прямую b иногда называют следом плоскости β на плоскости α. Признак параллельности прямых и плоскостей Теорема Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Доказательство Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана. 32)параллельное проектирование и его свойства Изображение на плоскости пространственных фигур обычно осуществляется с помощью параллельного проектирования этих фигур на некоторую плоскость. При этом должны выполняться следующие правила изображения, вытекающие из свойств параллельного проектирования: 1. Если прямая не параллельна проектирующей и не совпадает с ней, то проекция этой прямой есть прямая. 2. Проекции параллельных прямых, не параллельных проектирующей, параллельны или совпадают. 3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков. 33) ортогональное проецирование Направление проецирования перпендикулярно (ортогонально) плоскости проекций S Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести:
Рис. 1.10. Пример инвариантного свойства 9
Рис. 1.11. Ортогональная проекция прямого угла а) простоту графических построений для определения ортогональных проекций точек; б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей. Для ортогонального проецирования справедливы все девять инвариантных свойств, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования. 10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11) На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций π1. По инвариантному свойству 9 этот угол проецируется на плоскость π1 без искажения, т. е. Возьмем на проецирующем луче DD1 произвольную точку С, тогда полученный Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций π1, будет прямой угол А1В1D1. 34)перпендикулярность прямых в пространстве Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности. Перпендикулярные прямые Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла. В аналитическом выражении прямые, заданные линейными функциями Для обозначения перпендикулярности имеется общепринятый символ: [править]Построение перпендикуляра
Построение перпендикуляра Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А' и В'. Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A' и В' соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q. Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ. [править]Координаты точки основания перпендикуляра к прямой A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp). xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya. Признак перпендикулярности прямой и плоскости
35)теорема о трёх перпендикулярах
36) признак перпендикулярности плоскостей
37) связь между параллельностью и перпендикулярностью плоскостью Определение 3.3. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости. Доказательство Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Две плоскости, перпендикулярные одной прямой, параллельны между собой.
Докажите эти теоремы самостоятельно, используя такое свойство: если векторы
Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.
38) двугранный угол Двугранный угол
Двугранный угол – это часть пространства, заключенная между двумя полуплоскостями, имеющими одну общую границу.
Полуплоскости α и β, образующие двугранный угол, называются его гранями (чертеж 3.6.1). Общая прямая этих граней называется ребром двугранного угла. Пусть точки A и B взяты на ребре двугранного угла. Двугранный угол обозначается двумя буквами: угол AB. Иногда двугранный угол обозначается четырьмя буквами, из которых две средних обозначают точки ребра, а две крайние – точки, взятые на гранях. Пусть M
При пересечении двух плоскостей образуются четыре двугранных угла. Величина меньшего из этих двугранных углов называется углом между этими плоскостями. Если плоскости параллельны, то угол между ними равен 0° по определению. Если φ – величина угла между двумя плоскостями, то 0° < φ < 90°.
Угол между плоскостям Угол между плоскостями Пусть плоскости Плоскости, пересекаясь, образуют четыре двугранных угла (рис. 11.6): два тупых и два острых или четыре прямых, причем оба тупых угла равны между собой, и оба острых тоже равны между собой. Мы всегда будем искать острый угол. Для определения его величины возьмем точку
Рис.11.6.Угол между плоскостями
40) параллелепипед и его свойства Параллелепи́пед (от греч. παράλλος — параллельный и греч. επιπεδον — плоскость) — призма, основанием которой служитпараллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них параллелограмм. § § Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. § Противолежащие грани параллелепипеда параллельны и равны. § Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений. 41) призма и её свойства |Викисклад=Category:Prisms (geometry) |Викисловарь=призма }} Призма (от др.-греч. πρίσμα (лат. prisma) «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными)многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы § § Боковые грани призмы являются параллелограммами. § Боковые ребра призмы параллельны и равны. § Объём призмы равен произведению её высоты на площадь основания:
§ Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания. § Площадь боковой поверхности произвольной призмы § Площадь боковой поверхности правильной призмы § Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы. § Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах. § Перпендикулярное сечение перпендикулярно ко всем боковым граням. 1. площадь поверхности и объем Формулы объёма — например, объём куба или объём призмы — и формулы площади поверхности. 2. Элементарная логика. Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
42)пирамида § Пирамида — тип многогранников. § Пирамида — вид архитектурного сооружения в форме пирамиды. § Энергетическая пирамида — термин, применяющийся в культуре Нью-эйдж и эзотерике. § Пирамида — официальное название игры в русский бильярд. § Финансовая пирамида — способ получения дохода за счёт постоянного расширяющегося привлечения денежных средств от новых участников. § Пирамида — элемент художественной, силовой и пластической акробатики, групповое расположение акробатов, которые, поддерживая друг друга, образуют сложные фигуры. § Пирамидка — головоломка, прототипом которой был Кубик Рубика. § Tetra Classic — пирамидальная форма упаковки для жидкостей (молочных продуктов, соков). Географические объекты: § Пирамида — остров в составе Алеутских островов. § Пирамида — русский шахтёрский посёлок на Свальбарде (Шпицберген). Постройки: § Египетские пирамиды — архитектурные памятники Древнего Египта. § Пирамида — один из первых павильонов пейзажной части Екатерининского парка в Царском Селе. § Фонтан «Пирамида» — фонтан в Нижнем парке Петергофа. § Пирамиды Голода — пирамиды, построенные из стеклопластика в пропорциях золотого сечения инженером Александром Голодом. Схемы и диаграммы: § Пирамида здорового питания — диаграмма, схематическое представление принципа здорового питания. § Пирамида капиталистической системы — плакат 1911 года. Названия: § Пирамида — команда КВН из Владикавказа. § Пирамида — кинотеатр в Махачкале. Художественные произведения: § Пирамида — роман британского писателя У. Голдинга. § Пирамида — роман русского писателя Л. М. Леонова. § Пирамида (Кадаре) (англ.)русск. — роман албанского писателя И. Кадаре. § Пирамиды — роман Терри Пратчетта. § ПираМММида — фильм. Площадь поверхности и объём бъем наклонной призмы V=Sпсa, где Sпс - площадь перпендикулярного сечения наклонной призмы, a - боковое ребро. Площадь боковой поверхности наклонной призмы Sб=Pпсa, где Pпс - периметр перпендикулярного сечения наклонной призмы, a - боковое ребро. Площадь полной поверхности наклонной призмы Sп=Sб+2Sосн, где Sб, - площадь боковой поверхности наклонной призмы, Sосн - площадь её основания. Прямая призма
V=Sоснa, где Sосн - площадь основания прямой призмы, a - боковое ребро. Площадь боковой поверхности прямой призмы Sб=Pоснa, где Pосн - периметр основания прямой призмы, a - боковое ребро. Площадь полной поверхности прямой призмы Sп=Sб+2Sосн, где Sб, - площадь боковой поверхности прямой призмы, Sосн - площадь основания. Прямоугольный параллелепипед
V=abc, где a,b,c - измерения прямоугольного параллелепипеда. Площадь боковой поверхности параллелепипеда Sб=2c(a+b), где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда. Площадь полной поверхности прямоугольного параллелепипеда Sп=2(ab+bc+ac), где a,b,c - измерения прямоугольного параллелепипеда.
Куб V=a3, Sб=4a2, Sп=6a2, где a - ребро куба. Пирамида Объем пирамиды
где Sосн - площадь основания, H - высота. Sп=Sб+2Sосн, где Sб - площадь боковой поверхности прямой пирамиды, Sосн - площадь основания.
где Pосн - периметр основания правильной пирамиды, l - её апофема. Усеченная пирамида Объем усеченной пирамиды
где S1 , S2 - площади оснований усеченной пирамиды, H - её высота. Sп=Sб+S1+S2, где Sб - площадь боковой поверхности пирамиды, S1 , S2 - площади оснований.
где P1 , P2 - периметры оснований, а l - ее апофема. Цилиндр Объем цилиндра V=p R 2H, где R - радиус основания цилиндра, а H - его высота. Sб=2p R H, где R - радиус основания цилиндра, а H - его высота. Sп=2p R H + 2p R2, где R - радиус основания цилиндра, а H - его высота. Конус Объем конуса
где R - радиус основания конуса, а H - его высота. Sб=2p R L, где R - радиус основания конуса, а L - его образующая. Sп=2p R (R+L), где R - радиус основания конуса, а L - его образующая. Усеченный конус Объем усеченного конуса
где R, r - радиусы оснований усеченного конуса, Н - его высота. Sб=p L (R+r), где R, r - радиусы оснований усеченного конуса, L - его образующая. Sп=p L (R+r)+p R2+p r2, где R, r - радиусы оснований усеченного конуса, L - его образующая. Сфера и шар Объем шара
где R - радиус шара S=4p R2, где R - радиус сферы
где H - высота шарового сегмента, R - радиус шара
43) Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, основание которого —многоугольник, а остальные грани — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса. § около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр; § боковые ребра образуют с плоскостью основания равные углы. § также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
44) Усеченная пирамида или конус -это часть, остающаяся после отсечения вершины плоскостью, параллельной основанию. Объем усеченной пирамиды или конуса равен объему целой пирамиды или конуса минус объем отсеченной вершины. Площадь боковой поверхности усеченной пирамиды или конуса равна площади поверхности целой пирамиды или конуса. минус площадь боковой поверхности отсеченной вершины. Если необходимо найти общую площадь усеченной фигуры, тогда площадь двух параллельных оснований добавляется к площади боковой поверхности. Существует и другой метод определения объема и площади поверхности усеченного конуса:
площадь боковой поверхности конуса S=π l(R+r), общая площадь поверхности Sо=π l(R+r)+πr2+πR2
Пример1. Определение площади необходимого для изготовления материала для абажура. (Расчет площади боковой поверхности конуса).
Абажур имеет форму усеченного конуса. Высота абажура равна 50 см, нижний и верхний диаметры - 40 и 20 см соответственно. Определить с точностью до 3х значащих цифр площадь материала, необходимого для изготовления абажура.
Поскольку верхний и нижний диаметры усеченного конуса равны 40 и 20 см, то из рис. выше находим r=10 см, R=20 см и l=(50 2+102)1/2=50,99 согласно теореме Пифагора, Следовательно, площадь боковой поверхности конуса равна S=π 50,99(20+10)=4803,258 см2, т.е. площадь необходимого для изготовления абажура материала равняется 4800 см2 с точностью до 3х значащих цифр, хотя, конечно, сколько на самом деле уйдет материала зависит от кроя.
Пример 2. Определение объема цилидра, увенчанного усеченным конусом.
Объем цилиндрической части V=π R2h =π(27/2)2*14=8011,71 м3 Объем усеченного конуса V=1/3 π h(R2+Rr+r2), где h=34-14=20 м, R=27/2=13,5 м и r=14/2=7 м. Т.к. R=27/2=13,5 м и r=14/2=7 м. Следовательно, объем усеченного конуса V=1/3 π 20(13,52+13,5*7+72)=6819,03 м3 Общий объем башенного охладителя Vобщ.=6819,03+8011,71=14830,74 м3. Если 40% объема занято, объем воздушного пространства V=0,6*14830,74=8898,44 м3 45) Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны. Теорема 9.4. Правильный многоугольник является вписанным в окружность и описанным около окружности, при этом центры этих окружностей совпадают. Доказательство Следствие 9.2. Центр правильного многоугольника совпад
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.212.225 (0.011 с.) |


 , где H — высота сегмента, а
, где H — высота сегмента, а  — зенитный угол
— зенитный угол
 — координаты центра сферы,
— координаты центра сферы,  — её радиус.
— её радиус.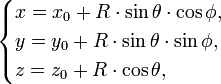
 и
и 




 и
и 
 , то прямые
, то прямые 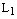 и
и  совпадают;
совпадают; , то прямые
, то прямые  , то прямые пересекаются.
, то прямые пересекаются. равносильно коллинеарности нормальных векторов данных прямых:
равносильно коллинеарности нормальных векторов данных прямых: . Поэтому, если
. Поэтому, если  и прямыепересекаются.
и прямыепересекаются.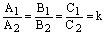 , то
, то  ,
,  ,
, 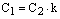 иуравнение прямой
иуравнение прямой 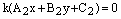 или
или  , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности
, т.е. прямые совпадают. Заметим, что коэффициент пропорциональности 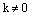 , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.
, иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.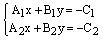 . (4)
. (4)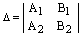 – определитель системы (4). Если
– определитель системы (4). Если 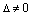 , то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера:
, то прямые пересекаются в одной точке и система (4) имеет единственное решение, которое можно найти по формулам Крамера: , (5)
, (5) ,
,  .
. , то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений.
, то прямые или параллельны и тогда система (4) не имеет решений, или прямые совпадают и тогда система (4) имеет бесконечно много решений. .
. и
и  и
и  , т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много.
, т.е. либо прямые параллельны и тогда система не может иметь ни одного решения, либо прямыесовпадают и тогда система (4) состоит из одного уравнения и решениями такой системы являются координаты любой точки, лежащей на прямой, а их бесконечно много. Теорема 2.4. Признак параллельности прямой и плоскости.
Теорема 2.4. Признак параллельности прямой и плоскости. Определение 2.4.
Определение 2.4.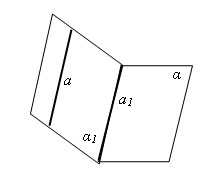
 π1 (рис. 1.11). Ортогональное проецирование является частным случаем параллельного проецирования.
π1 (рис. 1.11). Ортогональное проецирование является частным случаем параллельного проецирования. .
. .
. А1В1D1=90°.
А1В1D1=90°. и
и  будут перпендикулярны, если выполнено условие
будут перпендикулярны, если выполнено условие  . Эти же прямые будут перпендикулярны, если
. Эти же прямые будут перпендикулярны, если  . (Здесь
. (Здесь  — углы наклона прямой к горизонтали)
— углы наклона прямой к горизонтали)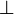 , предложенный в 1634 году французским математиком Пьером Эригоном.
, предложенный в 1634 году французским математиком Пьером Эригоном.


 . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости
. Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости 
 . Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости
. Прямая сперпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости 
 . Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости
. Она перпендикулярна прямой с, так как прямые а и bперпендикулярны, то плоскости 


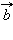 коллинеарные и
коллинеарные и  то
то 
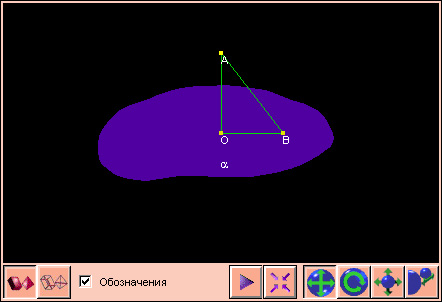

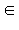 α, N
α, N 
 и
и  заданы соответственно уравнениями
заданы соответственно уравнениями  и
и  . Требуется найти угол
. Требуется найти угол  между этими плоскостями.
между этими плоскостями. на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры
на линии пересечения плоскостей и в этой точке в каждой из плоскостей проведем перпендикуляры  и
и 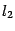 к линии пересечения. Нарисуем также нормальные векторы
к линии пересечения. Нарисуем также нормальные векторы  и
и  плоскостей
плоскостей 
 Параллелепипед симметричен относительно середины его диагонали.
Параллелепипед симметричен относительно середины его диагонали.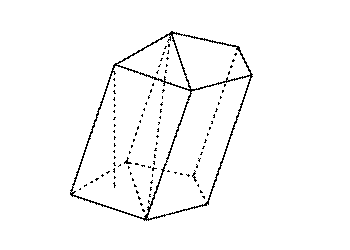 Основания призмы являются равными многоугольниками.
Основания призмы являются равными многоугольниками.
 , где
, где  — периметр перпендикулярного сечения,
— периметр перпендикулярного сечения,  — длина бокового ребра.
— длина бокового ребра. , где
, где  — высота призмы.
— высота призмы.

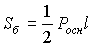

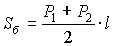







 V=1/3 π h(R2+Rr+r2),
V=1/3 π h(R2+Rr+r2),
 Башенный охладитель имеет форму цилиндра, увенчанного усеченным конусом, как показано на рис. ниже. Определить объем воздушного пространства в башне, если 40 % объема занято трубами и другими структурами.
Башенный охладитель имеет форму цилиндра, увенчанного усеченным конусом, как показано на рис. ниже. Определить объем воздушного пространства в башне, если 40 % объема занято трубами и другими структурами.


