Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действие над векторами и их свойстваСодержание книги
Поиск на нашем сайте
Ключевые слова: вектор, сумма, разность векторов, координаты вектора Вектор - это направленный отрезок. Суммой векторов − Для любых векторов −
Каковы бы ни были три точки A, B и C, имеет место векторное равенство −− Разностью векторов − Произведением вектора − Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними:
25) Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Обычно используется одно из следующих обозначений:
или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):
Обычно предполагается что скалярное произведение положительно определено, то есть
Если этого не предполагать, то произведение называется индефинитным.
26) прямоугольная система координат Прямоугольная система координат - прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению. Связанные термины: Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат (не прямоугольную). [1] Действие над векторами, заданными координатами Теорема 3. Пусть на плоскости выбран векторный базис и складываются или вычитаются их одноименные координаты; и складываются или вычитаются их одноименные координаты; Длина вектора Векторы Обозначения:
Сумма векторов:
Разность векторов: Формула вычитания векторов: Признак коллинеарности векторов: 27)векторы в пространстве и действия над ними Вектором наз. упорядоченная совокупность чисел Х ={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор - направленный отрезок. | AB |=| a | - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну. 1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А || В. б) l>0, то А В, l<0, то А ¯ В. в)l>1, то А <<span style="TEXT-DECORATION: underline">В,)l<1, то АВ. 2. Разделить вектор на число n значит умножить его на число, обратное n: а /n= a *(1/n). 3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а. Скалярное произведение Определение 9.15. Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так:
Скалярным произведением векторов
28) уравнение прямой и плоскости Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи: - C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат - А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох - В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу - В = С = 0, А ¹ 0 – прямая совпадает с осью Оу - А = С = 0, В ¹ 0 – прямая совпадает с осью Ох Уравнение сферы Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учетом непостоянства значения размеров дуг составляет 41252.96 кв. градусов. Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностьюшара. Объёмы цилиндра, вписанной в него сферы, касающейся его основания, и двух конусов, имеющих общую вершину в центре основания и основания, равные основаниям цилиндра, находятся в соотношении 1:2:3[1] Площадь сферы
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.006 с.) |

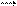 a (a 1; a 2) и −
a (a 1; a 2) и − 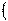 a 1+ b 1; a 2+ b 2
a 1+ b 1; a 2+ b 2  ,
, 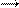 a (a 1; a 2) и −
a (a 1; a 2) и − 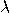 называется вектор −
называется вектор −  −
−  −
−  , если угол между векторами равен
, если угол между векторами равен  ,
, ,
, ,
, .
. для всех
для всех  .
. ,
, 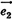 и относительно него векторы
и относительно него векторы 
 заданы своими координатами:
заданы своими координатами:  . Тогда
. Тогда  , т. е. при сложении или вычитании векторов
, т. е. при сложении или вычитании векторов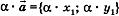 , т. е. при умножении вектора на число его координаты умножаются на это число.
, т. е. при умножении вектора на число его координаты умножаются на это число. Длина вектора, модуль (абсолютная величина):
Длина вектора, модуль (абсолютная величина): 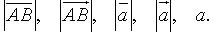

 (правило треугольника) (рис. 1.22);
(правило треугольника) (рис. 1.22); (правило параллелограмма) (рис. 1.23);
(правило параллелограмма) (рис. 1.23); (правило многоугольника);
(правило многоугольника); (правило параллелепипеда,
(правило параллелепипеда, 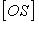 - диагональ).
- диагональ).
 (рис. 1.24).
(рис. 1.24).
 Определение 9.16.
Определение 9.16.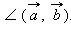
 и
и 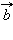 называется произведение их длин на косинус угла между ними:
называется произведение их длин на косинус угла между ними: