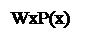Основные операции с объемами понятий

 

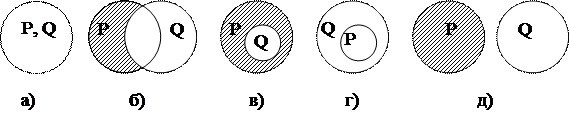
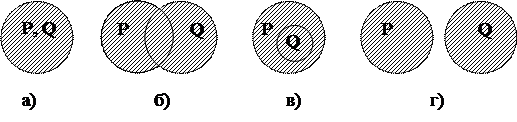
Основные операции с объемами и содержаниями понятий составляют часть так называемой теории множеств. К операциям с объемами понятий относятся пересечение, объединение, дополнение и вычитание.

Пересечение. С использованием языка логики предикатов операция пересечения запишется следующим образом:

WxP(x)ÇWxQ(x),

где W – оператор образования множества из понятия (оператор выделения объема понятия из самого понятия). W указывает на то, что речь идет именно об объемах понятий; Ç - знак пересечения.

Если мы ищем пересечение, то для разных видов совместимых и несовместимых понятий результаты пересечений их объемов получатся такими, как изображено на рисунке 5.

 

 

а) тождественные понятия;

б) перекрещивающиеся понятия;

в) подчиненное и подчиняющее понятия;

г) несовместимые (соподчиненные) понятия.

 

Рисунок 5. Пересечение

 

 

Объединение. Операция объединения запишется так:

WxP(x)ÈWxQ(x),

где È - знак объединения.

Различные варианты объединения объемов понятий изображены на рисунке 6.

Дополнение. Дополнением объема понятия хР(х) до универсума области возможных значений переменной х называется множество тех элементов этого универсума, которые не принадлежат понятию хР(х). Записывается дополнение следующим образом:

WxP(x)

Схема дополнения показана на рисунке 7.

 

 

а) тождественные понятия;

б) перекрещивающиеся понятия;

в) подчиненное и подчиняющее понятия;

г) несовместимые (соподчиненные) понятия.

 

Рисунок 6. Объединение

 

 

 

Рисунок 7. Дополнение

 

 

Вычитание: WxP(x)\WxQ(x),

где \ - знак вычитания объема одного понятия из объема другого.

Возможные варианты вычитания объемов понятий представлены на рисунке 8.

4.7 Основные операции с содержанием понятий

 

К основным операциям с содержаниями понятий относятся отрицание, конъюнкция и дизъюнкция.

Отрицание: WxùP(x) º WxP(x).

Конъюнкция:

а) Wx(P(x)ÙQ(x)) º WxP(x)ÇWxQ(x);

б) Wx(P(x)ÙùQ(x)) º WxP(x)\WxQ(x).

Дизъюнкция: Wx(P(x)ÚQ(x)) º WxP(x)ÈWxQ(x)

 

 

а) тождественные понятия;

б) перекрещивающиеся понятия;

в), г) подчиненное и подчиняющее понятия;

д) несовместимые (соподчиненные) понятия.

 

Рисунок 8. Вычитание

 

 

Диаграммы Венна

 

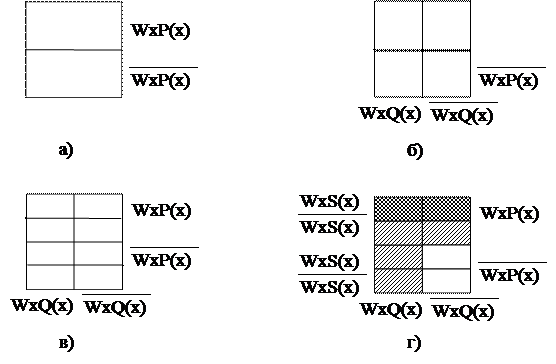
Диаграммы Венна используют для установления отношений между объемами понятий. Рассмотрим построение таких диаграмм на примере.

Допустим, нам нужно найти отношение между объемами понятий «детективный или фантастический роман» и «американский детективный роман». Используя оператор выделения объема (W), запишем их на языке логики предикатов:

1) Wx(P(x)ÚQ(x));

2) Wx(S(x)ÙP(x)),

где х – роман; Р – детективный; Q – фантастический; S – американский.

Полученные выражения преобразуем с помощью операций с содержаниями понятий:

1) Wx(P(x)ÚQ(x)) º WxP(x)ÈWxQ(x);

2) Wx(S(x)ÙP(x)) º WxS(x)ÇWxP(x).

Теперь построим диаграмму. Для этого начертим квадрат, изображающий универсум, т.е. область значений переменной х. Разделим его пополам по горизонтали. Пусть верхняя часть соответствует классу WxP(x), а нижняя – дополнению к нему WxP(x) (рис. 9, а)). Затем разделим квадрат по вертикали на части, соответствующие классам WxQ(x) и WxQ(x) (рис. 9, б)). Области, соответствующие классам WxS(x) и WxS(x) разместим на диаграмме так, как показано на рисунке 9, в). По-разному заштрихуем части диаграммы, соответствующие классам WxP(x)ÈWxQ(x) и WxS(x)ÇWxP(x) (рис. 9, г)).

На диаграммах мы видим, что объем второго понятия составляет часть объема первого, значит, понятия являются совместимыми и находятся в отношении подчинения. Причем первое понятие оказалось подчиняющим, а второе – подчиненным.

Отношение совместимых понятий на диаграммах Венна легко определить (занимаемые ими области располагаются аналогично кругам Эйлера). Что касается несовместимых понятий, для того чтобы установить вид отношения между ними, нужно знать следующие правила:

- объемы противоречивых понятий занимают на диаграмме разные места, исчерпывая всю ее площадь;

- объемы соподчиненных понятий занимают на диаграмме просто разные места, не исчерпывая ее площадь;

- объемы противоположных понятий занимают на диаграмме диагонально расположенные клеточки.

 

 

 

Рисунок 9. Построение диаграммы Венна

 

 

Определение понятий

 

Содержание и объем понятия зачастую скрыты за его словесной оболочкой. Поэтому в практике мышления нередко приходится раскрывать как содержание, так и объем понятий. Это позволяют сделать определение и деление понятий.

Определение – логическая операция, посредством которой раскрывается основное содержание понятия.

Русское слово «определение» (от слова «предел») представляет буквальный перевод с латинского definitio (от слова finis – конец, граница), которое, в свою очередь, есть также буквальный перевод с древнегреческого horismos (от слова horos – предел, граница, веха). Как свидетельствует наука, это слово вошло в широкий обиход в глубокой древности – в эпоху распада общинной собственности и установления частной собственности на землю. Первоначально им обозначалось разграничение земельных участков посредством вех, пограничных столбов. Впоследствии оно было распространено на мыслительную, логическую операцию, которая выделяла предмет мысли, как бы отмежевывала его, отграничивала в мыслях от других предметов.

Определение понятий решает две основные задачи:

1) отличает предметы, входящие в объем данного понятия, от всех остальных предметов;

2) раскрывает сущность соответствующего предмета. А поскольку понятие непременно выражается словом, то определение понятия есть вместе с тем раскрытие смысла слова.

От определений в узком собственном смысле слова следует отличать определения в широком смысле. В последнем случае, определением называется всякая квалификация предмета вообще: «Золото – металл», «Осел – животное» и т.п. Нас, прежде всего, интересуют определения в узком смысле слова.

Определения также нельзя смешивать со сходными операциями, которые часто называют приемами сходными с определением. К ним относят остенсивное определение, описание, характеристику, сравнение, разъяснение через пример.

Остенсивное определение – это демонстрация.

Описание – перечисление всех (существенных и несущественных) непосредственно выявленных свойств предмета. Недостаток описания – субъективный результат (разные люди по разному опишут любой предмет).

Характеристика – это выделение существенных в некотором отношении свойств предмета. Недостаток характеристики – односторонность.

Сравнение – установление сходства или отличия одного предмета от другого.

Разъяснение через пример – приведение примера, иллюстрирующего понятие. Скажем, если вас попросили объяснить, что такое «вежливость», но вы затрудняетесь дать ее определение, можно привести пример: вежливость – это когда здороваются со знакомыми.

В конечном счете, определение отвечает на вопрос: что такое данный предмет? Конечно, если содержание понятия нам известно из опыта («собака», «ложка», «карандаш»), то, как правило, нет необходимости в его определении. Однако в некоторых случаях определения необходимы. Во-первых, они нужны для подытоживания главного в познании сущности предмета. Например, если ученый исследует какое-либо природное явление, итогом может стать определение этого явления. Во-вторых, определения необходимы, когда употребляются такие понятия, содержание которых читателю или слушателю неизвестно. В-третьих, определения необходимы, если вводится в обиход новое слово или известное слово употребляется в новом значении и т.д.

Определения выполняют две важнейшие функции: познавательную и коммуникативную. Познавательная функция определения состоит в том, что в определениях закрепляются наиболее общие результаты познавательной, абстрагирующей деятельности человека. В то же время они служат средством дальнейшего познания, основой для понимания предмета. Коммуникативная функция заключается в том, что благодаря определению знания одних людей в процессе общения передаются другим. С их помощью предотвращается смешение понятий, достигается взаимопонимание, осуществляется духовная связь поколений.

В повседневном общении мы довольно редко прибегаем к определениям. А вот в науке и учебном процессе – это обязательное и частое явление. Хотя, с другой стороны, роль определений нельзя преувеличивать. Определение – основа для понимания предмета, но не все знания о нем.

Любое определение состоит из двух частей:

- дефиниендум (лат. definiendum) – определяемое понятие (dfd);

- дефиниенс (лат. definiens) – определяющее понятие (dfn).

 

Виды определений

 

По той функции, которую определения выполняют в познании, они делятся на номинальные и реальные.

Номинальные определения – это соглашения относительно смысла вновь вводимых языковых выражений, а также соглашения о том, в каком из различных имеющихся смыслов следует употреблять выражение в данном контексте. Результаты таких определений нельзя оценивать как истинные или ложные.

Пример. «Будем называть гомеостазом совокупность внешних условий, обеспечивающих возможность существования данного организма».

Реальные – это определения, в которых придается точный смысл выражениям, значения которых с большей или меньшей степенью определенности уже известны. Посредством реальных определений вводятся понятия о предметах, обозначаемых термином, т.е. решается задача выделения системы признаков, общей и отличительной для этих предметов.

Пример. «Шар – геометрическое тело, получаемое при вращении круга вокруг его диаметра».

По форме определения можно подразделить на явные и неявные.

Явными называются определения, в которых определяемое и определяющее понятия четко разделены, а их объемы равны. Форма явных определений: Wdfd=Wdfn.

Неявные определения такой формы не имеют.

 

Виды явных определений

 

Наиболее распространенная форма явных определений – определение через ближайший род и видовое отличие. Такие определения имеют множество разновидностей.

Генетические определения указывают способ образования, происхождения, конструирования определяемого предмета. Например: «Шар – геометрическое тело, получаемое при вращении круга вокруг его диаметра».

Сущностные определения (или определения качества предмета) широко применяются во всех науках. В таких определениях раскрывается сущность предмета, его природа или качество. Таковы определения сущности жизни, общества, человека, государства, науки, техники и т.д.

Функциональными определениями называются такие, в которых раскрывается назначение предмета, его роль и функции. Например: «Барометр – прибор для измерения атмосферного давления».

Структурные определения (или определения по составу). В них раскрываются элементы системы, виды какого-либо рода или чисти целого. Например: «Политическая система – совокупность государственных и негосударственных, партийных и непартийных организаций и учреждений».

Операционные определения указывают на идентифицирующую операцию, т.е. такую операцию, с помощью которой можно распознать определяемый предмет. Например: «Кислота – это жидкость, в которой лакмусовая бумажка окрашивается в красный цвет».

Заметим, что разные авторы дают различную классификацию видов явных определений. Так, Ю.В. Ивлев среди явных определений выделяет атрибутивно-реляционные, генетические и операционные.

Атрибутивно-реляционными он называет такие определения, которые указывают свойства (атрибут) или отношения (реляцию), т.е. признаки определяемого предмета. Например, «Хорда – это отрезок прямой, соединяющий две какие-нибудь точки окружности»; «Дерево – многолетнее растение, имеющее ствол, крону и корни».

Е.К. Войшвилло и М.Г. Дегтярев как важный вид явных определений выделяют также определения через абстракцию. Этот способ применяется для определения таких абстрактных объектов (предметно-функциональных характеристик предметов), как вес, форма, площадь, длина и т.п. Определение здесь осуществляется посредством особого типа отношений, называемых отношениями равенства (эквивалентности). Примерами таких отношений могут служить равновесомость, подобие (фигур), конгруэнтность отрезков. Например, «Форма геометрической фигуры есть то общее, что имеется у всех подобных фигур».

 

Виды неявных определений

 

К неявным определениям относятся определения через отношение к противоположному (соотносительные), аксиоматические и контекстуальные определения.

В определениях через отношение к противоположному для раскрытия содержания определяемого понятия используется противоположное ему понятие. Например: «Причина – это явление, которое при определенных условиях обязательно вызывает другое явление, называемое следствием». В этом определении понятие «причина» определяется через отношение к противоположному понятию «следствие».

Аксиоматическими называются определения, в которых содержание понятий задается системой аксиом, в которых это понятие встречается. Например, содержание понятий «точка», «прямая», «плоскость» в евклидовой геометрии задается аксиомами этой системы геометрии.

В контекстуальных определениях содержание понятия или смысл термина устанавливается не с помощью другого понятия или термина, а путем соотнесения его со всем контекстом.

Например, возьмем фрагмент из повести В. Курочкина «На войне как на войне»: «Очертили границу канонира, взяли лопаты и стали соскребать снег. Работали молча, остервенело… Саня едва стоял на ногах. – Головой ручаюсь, что это мартышкин труд. Вот увидите – завтра с рассветом отсюда уедем, - сказал наводчик». Даже если не знать, что такое «мартышкин труд», из контекста ясно, что это – бесполезная тяжелая работа.

Иногда говорят, что контекстуальными являются такие определения, в которых некоторый контекст использования определяемого понятия приравнивается к другому контексту, в который определяемое понятие не входит. Например, операция возведения в квадрат в арифметике определяется контекстуально: а² = а _* а.

 

Правила определения

 

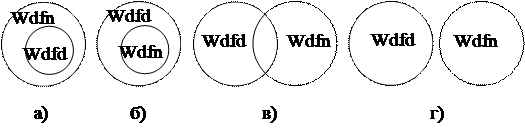
1. Объемы дефиниендума и дефиниенса должны совпадать (правило соразмерности). Другими словами, определяемое и определяющее понятия должны быть тождественными.

Ошибки, возможные при нарушении этого правила:

а) Широкое определение. Данная ошибка заключается в том, что объем определяемого понятия меньше объема определяющего: Wdfd<Wdfn (рис. 10, а)).

Пример. «Автократия – это форма правления, при которой государственная власть сосредоточена в руках одного лица». В этом определении совершена ошибка слишком широкого определения, потому что объем понятия «форма правления, при которой государственная власть сосредоточена в руках одного лица» включает в себя не только автократию, но и конституционную монархию. Разница между ними в том, что при автократии государственная власть сосредоточена в руках одного лица полностью (что и надо было отметить в определении), а при конституционной монархии – частично.

б) Узкое определение. В противоположность первой, ошибка «узкое определение» возникает, когда объем определяемого понятия больше объема определяющего: Wdfd>Wdfn (рис. 10, б)).

Пример. «Знак – материальный предмет, замещающий другой материальный предмет». В этом определении совершена ошибка узкого определения, потому что знаки, как мы уже знаем, могут замещать не только материальные, но и нематериальные объекты.

в) Перекрещивание. Эта ошибка совершается в том случае, если определяемое и определяющее понятия находятся в отношении перекрещивания, т.е. их объемы частично совпадают (рис. 10, в)).

Пример. «Нож – холодное оружие». В этом определении понятия «нож» и «холодное оружие» являются перекрещивающимися.

г) Определение как попало. Данная ошибка означает, что в качестве определяющего использовано понятие несовместимое (соподчиненное) с определяемым (рис. 10, г)).

Пример. Говорят, когда известный естествоиспытатель Кювье однажды зашел в Академию наук в Париже, где работала комиссия по составлению энциклопедического словаря, ему предложили оценить следующее определение: «Рак – небольшая красная рыбка, которая ходит задом наперед». Кювье сказал, что определение превосходно, если не считать того, что рак не рыба, он не красный и он не ходит задом наперед.

2. Определение не должно заключать в себе круга. Совершаемая при нарушении этого правила ошибка называется «круг в определении», и заключается в том, что сначала одно понятие определяется через другое, а затем второе – через первое.

Пример. «Логика – наука о правильном мышлении, а правильное мышление – это логическое мышление».

Обратите внимание, что для ошибки «круг в определении» необходимо, по крайней мере, два определения. Могут быть круги, состоящие из более чем двух определений, но они встречаются реже.

Частный случай этой ошибки – тавтология (непосредственный круг). Она имеет место в тех ситуациях, когда в наличии есть только одно определение, и заключается в попытке определить некоторый термин через самого себя(хотя, возможно, и в сочетаниями с другими терминами).

Пример. «Государство – это организация государственной власти», или «Светлые объекты – это объекты, которые светятся».

 

 

 

 

Рисунок 10. Ошибки, возникающие при нарушении правила соразмерности

 

 

3. Определение должно быть ясным. Суть этого правила в том, что должны быть известны смыслы или значения терминов, входящих в определяющее понятие. В частности, оно не должно содержать выражений, в сою очередь, требующих определения. При нарушении этого правила возникает ошибка неясное определение.

Пример. «Красота есть индивидуально неповторимое выражение родового».

Кроме того, если в качестве определения рассматриваются высказывания, содержащие метафоры, то такие определения также оказываются неясными.

Пример. «Повторенье – мать учения», «Лев – царь зверей».

4. Определение по возможности не должно содержать в определяющем понятии отрицательных признаков. Нарушение этого правила приводит к ошибке «использование отрицательного признака без необходимости».

Пример. Высказывание «Республика – это форма правления, не являющаяся монархией» является совершенно правильным. Но, если его рассматривать в качестве определения, то, как определение, оно не выполняет задачу сообщения существенной информации об определяемом понятии. Причем, определение не выполняет этой задачи, именно потому, что является отрицательным. Определяя республику через отрицательный признак «не быть монархией», мы почти ничего не узнаем о самой республике.

Тем не менее, часто очень трудно или даже невозможно избежать использования отрицательных признаков в определяющей части.

Пример. В определении «Автократия – это монархия, в которой отсутствуют подлинно представительные учреждения» используется отрицательный признак «отсутствие подлинно представительных учреждений», но избежать его использования практически невозможно.

5. Номинальные определения нельзя принимать за реальные. Истолковывая номинальные определения в качестве реальных, к ним добавляют новую, не содержащуюся в них информацию, например, о существовании предметов, обозначаемых определяемым понятием. Результатом такого истолкования могут стать ложные утверждения.

Пример. Из определения «Совершенное существо – то, которое обладает всеми свойствами объективно существующего предмета, а также свойствами всеведения и всемогущества» нельзя делать вывод, что совершенное существо реально существует.

6. Определение должно раскрывать лишь основное содержание определяемого термина.

Пример. В определении «Изомеры – это вещества, имеющие одинаковый состав молекул (одну и ту же молекулярную формулу), но различное химическое строение и обладающие поэтому (по крайней мере, некоторыми) различными химическими свойствами» признак «обладающие (по крайней мере, некоторыми) различными химическими свойствами» является лишним, если раньше в тексте сказано, что вещества, имеющие различное химическое строение, обладают (по крайней мере, некоторыми) различными химическими свойствами.

7. В научных определениях требуется раскрыть существенные стороны предметов. Иногда, ставя вопрос о том, что представляет собой тот или иной предмет, имеют в виду указание какой-либо отличительной совокупности его признаков. Однако под реальным определением имеют в виду ответ на вопрос, что представляют собой предметы по существу, в чем состоит основа их качественной специфики.

Пример. Требованию указать отличительную совокупность признаков человека, очевидно, удовлетворяет определение его как существа, способного плакать (имея в виду эмоциональный плач, а не рефлекторное выделение слез, которое возможно у многих животных). Однако оно не может считаться удовлетворительным как реальное определение.