
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие индекса. Основные элементы индекса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Классификация индексов. Взаимосвязь между индексами.
Вопрос 1. Индекс (index) латинского происхождения и переводится как указатель, показатель. В статистике индексами называют относительные показатели, характеризующие изменение сложных общественных явлений, элементы которых не поддаются непосредственному суммированию. Для характеристики изменений таких сложных явлений применяют индексы различных видов и форм, построенные на основе абстрагирования, выявления и установления причинно-следственных связей и отношений. Для определения индекса надо произвести сопоставление не менее двух величин. При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение, - за базисный (плановый) период. Результат расчета индекса может выражаться в коэффициентах или процентах (например индекс цен равен 1,1 или 110%, означает, что цены возросли на 10%). Основными элементами индекса являются: 1. Собственно индекс: индивидуальный (принято обозначать i) или сложный (I), 2. Соизмерители (в качестве соизмерителей могут выступать признаки, имеющие объемное (количественное) или качественное содержание). 3. Веса (в качестве весов также могут выступать количественные (объемные) и качественные показатели). 4. Индексируемая величина - это значение признака статистической совокупности, изменение которого является объектом изучения. Например, при изучении изменении цен индексируемой величиной является цена единицы товара р, при изучении изменения физического объема товарной массы в качестве индексируемой величины выступают данные о количестве товаров в натуральных измерителях q. Основными элементами индивидуального индекса являются: 1. собственно индекс индивидуальный индекс физического объема продукции индивидуальный индекс цен 2. индексируемая величина (для 1-го индекса будет количество товара в натуральном измерении q, для 2-го индекса - цена единицы товара р). Знак внизу справа означает период: 0 - базисный, 1 - отчетный. При построении сложных индексов, отражающих влияние объемного (количественного) показателя на изменение сложного общественного явления основными элементами индекса являются: 1. Собственно индекс индекс физического объема продукции (в агрегатной форме)
2. Индексируемые величины q1 и q0 3. Соизмерители - в качестве соизмерителей выступают неизменные цены базисного периода р0. При построении сложного индекса, отражающего влияние качественного показателя на изменение сложного общественного явления, основными элементами индекса являются: 1. Собственно индекс индекс цен (в агрегатной форме)
2. Индексируемые величины р1 и р0. 3. Веса - в качестве которых выступают данные об объемах продукции в текущем (отчетном) периоде q1. Вопрос 2. В статистике индексы классифицируются по ряду признаков: 1. по степени охвата явления 2. по базе сравнения 3. по форме построения 4. по составу явления 5. по содержанию индексируемых величин. 1. По степени охвата явления индексы подразделяются на: 1. индивидуальные - они характеризуют изменение отдельных единиц изучаемой совокупности (iq, iр) 2. сводные - это сложные индексы и они могут быть: а) общими - выражают обобщающие результаты совместного изменения всех единиц, образующих совокупность. б) групповыми (субиндексы) - охватывают только часть (группу) единиц в изучаемой совокупности. Примером сложного индекса может служить индекс стоимости продукции, который характеризует изменение стоимости продукции в отчетном периоде по сравнению с базисным за счет изменения q и р: 2. По базе сравнения различают: 1. Динамические индексы - используются для характеристики темпов изменений общественных явлений в динамике. Эти индексы в свою очередь подразделяются а базисные и цепные. Базисными называют индексы, при исчислении которых данные всех периодов сравниваются с одним периодом, взятым за базу, обычно с начальным периодом. Цепными называют индексы, при исчислении которых данные каждого периода сравниваются с данными предшествующего периодов. В цепных индексах база переменная. Базисные и цепные индексы могут быть индивидуальными и общими. Индивидуальные базисные и цепные индексы представляют собой разновидность базисных и цепных относительных величин динамики - и способы их расчета поэтому тождественны. Вычисление общих (базисных и цепных индексов) имеет свои особенности. Различают общие (базисные и цепные) индексы с постоянными и переменными весами. При вычислении индексов с постоянными весами в качестве весов для всего ряда принимаются соизмерители какого-либо одного периода (например, общие базисные индексы физического объема продукции с постоянными весами (в ценах 1991 года – р0):
общие цепные индексы физического объема продукции с постоянными весами (в ценах 1991 года – р0):
При исчислении индексов с переменными весами в качестве весов каждый раз принимаются соизмерители другого периода (например, общие цепные индексы цен с переменными весами:
2. Индексы выполнения плановых заданий. При их построении необходимо учесть плановое задание и фактическое его выполнение. Так для определения уровня выполнения планового задания реализации товаров сопоставляются сумма фактической продажи товарной массы в отчетном периоде Sq1p1 и величина планового задания продажи товаров в тех же ценах отчетного периода Sqплp1:
3. Территориальные индексы. Индексы могут использоваться для различных экономических сравнений не только в динамике, но и в территориальном разрезе за один и тот же период (например, сравнение районов по объему производимой продукции). В таких случаях прибегают к построению так называемых территориальных индексов.
3. По форме построения общие индексы делят на: 1. Агрегатные индексы 2. Средние индексы. Основной формой общих индексов являются агрегатные индексы. Агрегатным он называется потому, что числитель и знаменатель его представляют набор разнородных элементов. Агрегатный индекс рассчитывается как отношение суммы произведений индексируемых величин сравниваемых периодов на веса (величины, с помощью которых суммируются разнородные элементы). К агрегатным индексам относятся индекс физического объема продукции: а) индекс физического объема продукции в сопоставимых (базисных ценах)
При разности числителя и знаменателя индекса получаем абсолютный прирост суммы товарооборота в текущем периоде по сравнению с базисным периодом в сопоставимых (базисных) ценах за счет изменения физического объема реализованной продукции: SDqр(q)= Sq1p0 - Sq0p0. б) индекс физического объема продукции в ценах текущего периода
При разности числителя и знаменателя индекса получаем абсолютный прирост фактического товарооборота в текущем периоде по сравнению с расчетным при продаже количества товаров базисного периода по ценам текущего периода: SDqp(q)= Sq1p1 - Sq0p1. индекс цен:
Показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным периодом определяется как разность между числителем и знаменателем индекса: SDqp(p)= Sp1q1 - Sp0q1, т.е. изменение цен на данный ассортимент товаров в среднем обусловило изменение (увеличение / уменьшение) объема товарооборота в текущем периоде.
индекс стоимости продукции: Абсолютный прирост суммы товарооборота за счет совокупного действия факторов количества (q) и цен (р) определяется по формуле:
Таким образом, для исчисления агрегатного индекса необходимы два рода показателей: индексируемые величины и веса. Но практически эти показатели имеются не всегда. В таких случаях агрегатные индексы преобразуются в средние индексы: средний арифметический или средний гармонический. Преобразуем агрегатный индекс физического объема продукции в среднеарифметический. Как известно, формула индекса физического объема продукции имеет вид:
Для преобразования используем индивидуальный индекс индексируемой величины
Для преобразования агрегатного индекса цен в средний гармонический используем индивидуальный индекс индексируемой величины Заменив в формуле агрегатного индекса цен
4. По составу явления индексы бывают: 1. Постоянного (фиксированного) состава 2. Переменного состава. Часто при помощи индексов изучают динамику средних показателей. Изменение средней величины от того или иного показателя зависит: а) от изменения значения каждой отдельной единицы изучаемого явления, б) от изменения структуры явления. (например, средняя цена продажи товара зависит от уровня цен на товар и его удельного веса в объеме продаж; средний рост урожайности зерновых культур зависит от повышения урожайности каждой отдельной культуры и от увеличения ее удельного веса в общей площади более урожайных культур). Индекс, характеризующий совместное влияние указанных факторов (в котором меняются обе эти величины), называется индексом переменного состава:
где f- вес (доля) изучаемого признака. Например, индекс средних цен:
Индекс, характеризующий влияние только индексируемой величины (в котором меняется только эта величина), называется индексом постоянного состава:
Например, индекс средних цен постоянного состава:
Чтобы изучить влияние изменения структуры на изменение средней величины, исчисляют индекс структурных сдвигов:
где d – доля (удельный вес) продукции в общем объеме. Например, индекс влияния структурных сдвигов в реализованной продукции на изменение средней цены:
Вопрос 3. Взаимосвязь между индексами: 1. Произведение общих цепных индексов дает базисный индекс последнего периода. Пусть мы имеем 3 периода 1991, 1992, 1993.
Эта взаимосвязь имеет место лишь в цепных индексах физического объема (индексах с постоянными весами). В индексах цен, так же и в других индексах с переменными весами, такой взаимосвязи нет. 2. Отношение последующего базисного индекса к предшествующему равно цепному индексу последующего периода:
3. Поскольку величина объема продукции равна произведению количества продукции на цену, то индекс физического объема (Iq), умноженный на индекс цен (Ip) дает индекс стоимости продукции в фактических ценах (Iqp):
4. Индекс изменения средней величины (Iпер) равен произведению индекса в неизменной структуре (Iпост) на индекс, отображающий влияние изменения структуры явления на динамику средней величины (Iстр):
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3034; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |




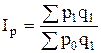
 .
. ;
; 

 ;
; 






 ;
;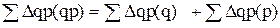 .
.
 , отсюда
, отсюда 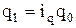 . Заменив в формуле агрегатного индекса физического объема продукции
. Заменив в формуле агрегатного индекса физического объема продукции  на
на 
 .
. , отсюда
, отсюда 
 равной ей величиной
равной ей величиной  , получим формулу среднего гармонического индекса цен:
, получим формулу среднего гармонического индекса цен: .
. ,
, - осредненный признак
- осредненный признак
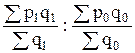 .
.
 .
. ,
, .
. .
. .
. .
. или
или 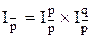 .
.


