
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Экстраполяция по темпу роста.Содержание книги
Поиск на нашем сайте Возможны два варианта экстраполяции по темпу роста.
Вариант А. Прогнозное значение определяется по формуле:
где
Вариант Б. Если имеется динамика за ряд предшествующих периодов, то можно использовать усредненный темп роста:
IV. Аппроксимация динамического ряда аналитическими функциями – расчет параметров (а, b, с) для конкретной функциональной зависимости. Параметры модели тренда должны минимизировать отклонения расчетных значений от соответствующих значений исходного ряда. Выбор модели осуществляется с помощью специально разработанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16-ти функциям: линейной (y = а + b * х), гиперболической различных типов (у = а + b / х), экспоненциальной, степенной, логарифмической и др. Каждая из них может иметь свою, специфическую область применения при прогнозировании экономических явлений.
Так, линейная функция применяется для описания процессов, равномерно развивающихся во времени. Параметр b (коэффициент регрессии) показывает скорость изменения прогнозируемого у при изменении х. Гиперболы хорошо описывают процессы, характеризующиеся насыщением, когда существует фактор, сдерживающий рост прогнозируемого показателя.
Модель выбирается, во-первых, визуально, на основе сопоставления вида кривой, ее специфических свойств и качественной характеристики тенденции экономического явления; во-вторых, исходя из значения критерия. В качестве критерия чаще всего используется сумма квадратов отклонений – из совокупности функций выбирается та, которой соответствует ее минимальное значение.
Для окончательного выбора вида функции нужно исследовать логику протекания процесса в целом, в том числе гипотезы его протекания в перспективе. Игнорирование этого этапа приводит к ошибочным, а иногда к парадоксальным выводам. Вы должны ответить на следующие вопросы: -является ли исследуемый показатель величиной монотонно возрастающей, монотонно убывающей, стабильной или периодической; -ограничен ли сверху или снизу исследуемый показатель каким-либо пределом; -имеет ли функция, определяющая процесс, точку перегиба; -обладает ли функция, описывающая процесс, свойством симметричности; -имеет ли процесс четкое ограничение развития во времени?
Выбор функции, применяемой для описания явления, зависит от типа динамики процесса. Далее будут приведены основные элементарные функции прогнозной экстраполяции. Прогноз предполагает продление тенденции прошлого, выражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда. Программным путем на ЭВМ определяется значение прогнозируемого показателя. Для этого в формулу, описывающую процесс, подставляется величина периода, на который необходимо получить прогноз. В связи с тем, что этот метод исходит из инерционности экономических явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существенных изменений в будущем, его целесообразно использовать при разработке краткосрочных прогнозов обязательно в сочетании с методами экспертных оценок. Причем динамический ряд может строиться на основании данных не по годам, а по месяцам, кварталам. При аппроксимации динамического ряда известными аналитическими функциями предполагается, что для прогнозирования будет использована функция, у которой форма кривой ближе всего подходит к графическому тренду. Самый простой способ выбора функции – визуальный, на основе графического изображения динамического ряда. Чаще всего для аппроксимации используются: -линейная функция -парабола -гипербола -логарифмическая функция -экспоненциальная функция -степенная функция -показательная
Для определения значений эмпирических коэффициентов
где
Так для линейной функции имеем:
Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдем неизвестные эмпирические коэффициенты:
При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра
где
Таблица 2.4 Значения коэффициента доверия по распределению Стьюдента
Для параболы
Скорость старения данных характеризует параметр сглаживания а. Он изменяется в пределах 0 < а < 1. Чем больше а, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убывает. В области экономического прогнозирования наиболее употребимы пределы 0,05 < а < 0,3. Значение а в общем случае должно зависеть от срока прогнозирования: чем меньше срок, тем большим должно быть значение параметра.
Методы моделирования
1. формулировка цели прогнозного исследования; 2. выделение в объекте прогнозирования структурных элементов, оказывающих влияние на характер и динамику его развития; 3. выявление внешних факторов, влияющих на развитие объекта прогнозирования; 4. логическое описание взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами (построение информационной модели); 5. формализация (математическое описание) взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами (показателями); 6. проведение расчетов, корректировка и уточнение модели.
-возможность отражения многосторонних связей между результирующими и влияющими факторами; -возможность использования экономико-математических моделей при управлении экономическими процессами и при поиске наиболее эффективных (оптимальных) управленческих решений.
-экономико-статистические; -структурные; -оптимизационные; -имитационные и др.
По аспектам развития экономики выделяют модели прогнозирования воспроизводства основных фондов, трудовых ресурсов, цен и др.
Экономико-статистические модели представляют собой вид моделей, описывающих с помощью уравнений регрессии зависимости между входными и результирующими факторами. Различают однофакторные и многофакторные модели. Многофакторные модели позволяют изучать влияние на объект прогнозирования нескольких факторов, однофакторные – одного. Начальным этапом построения модели является отбор влияющих факторов. Влияние факторов может описываться уравнениями следующих видов:
-линейные -степенные -логарифмические
- -
Экономико-статистические модели являются одним из основных инструментов управления социально-экономическими процессами и часто используются при поиске наиболее эффективных решений.
Раздел 3. Методология планирования Тема №5: Методы планирования 1.Система методов планирования 2.Прогнозирование и формирование темпов, пропорций и структуры экономики в условиях рынка 3.Прогнозирование уровня жизни населения
1.Система методов планирования
Методы планирования представляют собой совокупность способов и приёмов с помощью которых обеспечивается разработка и обоснование плановых документов. Система методов планирования включает в себя: нормативный, программно-целевой, балансовый и графический методы.
-Нормативный метод планирования
Норма – это научно обоснованная мера затрат ресурса на изготовление единицы продукции в конкретных производственно-технических условиях. Нормативы отражают общественные требования к результатам деятельности и характеризуют необходимый уровень использования ресурса. Комплекс норм и нормативов, используемых для разработки плановых документов, называется нормативной базой. Сам по себе нормативный метод самый лёгкий и простой в применении из всех остальных методов планирования. Так, например, если норма времени на изготовление изделия – 10 часов ( Основная сложность при применении нормативного метода заключается в определении величины нормы. Существуют следующие основные методы разработки норм и нормативов: 1. научного обоснования; 2. аналитически-расчетный; 3. аналитически-исследовательский; 4. опытный; 5. отчетно-статистический.
Пример. Магазин закупает хлеб на хлебозаводе по цене 10 рублей за батон, а продает по 11 руб. Если хлеб не будет реализован в день завоза, то на следующий день его продают по 8 рублей за батон (с одой стороны это связано с ухудшением качества продукции, а с другой стороны, присутствует определённый элемент рекламы). Необходимо определить ежедневную норму завоза хлеба, обеспечивающую максимум прибыли. Данные об объемах реализации хлеба в течение прошлой недели представлены в табл. 3.1.
Таблица 3.1 Объемы реализации хлеба в течение недели
Решение.
Номинальная прибыль от реализации хлеба составляет:
Обозначим вероятность продажи
С другой стороны, ожидаемый убыток связанный с не реализацией (а значит с ухудшением качества)
где Для определения оптимальной нормы завоза необходимо уравновесить ожидаемую прибыль и убыток:
Отсюда, вероятность реализации хлеба:
Значит, ежедневная норма завоза хлеба должна составлять такое количество буханок, вероятность продажи которых равна 0,67 или 67%. Будем считать, что исследуемое нами явление, как и большинство других экономических процессов подчиняется нормальному закону распределения. Тогда с ростом нормы завоза хлеба вероятность реализации всего завоза будет уменьшаться по зависимости изображенной на рис. 3.1.
Таким образом, величину нормы можно определить из выражения:
где
Соответственно, ежедневная норма завоза хлеба:
Существует достаточно большое количество разнообразных примеров применения метода научного обоснования нормы. При этом, с целью определения оптимальной (по определенному критерию) нормы могут использоваться экономико-статистические, оптимизационные и другие модели. - Аналитически-расчётный метод основан на разделении выполняемых работ на составные элементы с последующим их анализом и проектированием рациональных вариантов использования материальных ресурсов, оборудования и рабочей силы. Пример. Из прутка стандартной длины - 3 метра нарезаются заготовки вида А - 80 см и вида Б - 52 см. Применяемость данных заготовок в изделии: А – 2 шт., Б – 2 шт. Масса 1 метра погонного прутка 2,4 кг. Ширина распила – 5мм. Определить норму расхода материала на изделие. Решение. Рассмотрим возможные варианты распила прутка. Первоначально попытаемся нарезать как можно больше заготовок вида А (так как они самые длинные), а из оставшегося материала заготовки меньшей длины – Б. В последующих вариантах будем уменьшать количество нарезаемых заготовок вида А на одну единицу.
Вариант 1. 3 А и 1 Б, Отходы материала:
Вариант 2. 2 А и 2 Б, Отходы материала:
Вариант 3. 1 А и 4 Б, Отходы материала:
Вариант 4. 0 А и 5 Б, Отходы материала:
На первый взгляд самым подходящим является вариант №2. Из одного прутка данным способом можно вырезать 2 заготовки вида А и 2 вида Б, т.е., комплект заготовок на одно изделие. Следовательно, норма затрат материала – 3 метра погонных на изделие, или а) Рассмотрим сочетание 1 и 3-го вариантов. Обозначим
Значит, при сочетании 1 и 3 вариантов из 5 прутков - 3 следует разрезать 1-м способом, а 2 прутка 3-м способом. В этом случае мы получаем:
Норма:
б) Рассмотрим сочетание 1 и 4-го вариантов. Обозначим
Это значит, что из 7 прутков 1-м вариантом разрезаем 5, а 2-м – 2 прутка. Количество заготовок: Норма:
Анализ возможных вариантов распила прутков показывает, что наиболее целесообразным является сочетание 1 и 3 вариантов, так как в этом случае норма расхода материалов будет наименьшей (
-Аналитически-исследовательский метод основан на определении норм путем проведения наблюдений и экспериментов. Данный метод нашел широкое применение на действующих производствах. С помощью наблюдений, как правило, определяются нормы затрат времени на выполнение технологических операций. Часто в ходе наблюдений и экспериментов изучается возможность и оценивается целесообразность внедрения различных вспомогательных приспособлений, снижающих затраты времени на выполнение операций. Таким образом, практическое применение аналитическо-исследовательского метода направлено не только на определение значений нормируемых параметров, но и на совершенствование технологического процесса. -Отчётно-статистический метод заключается в том, что нормы затрат производственных ресурсов устанавливаются на основе отчётных или статистических данных за прошедшие периоды. Пример. Имеются отчетные данные по энергопотреблению цехом, выпускающим продукцию двух наименований (табл. 3.2).
Определить нормы затрат электроэнергии на изготовление продукции вида А и Б, а также, затраты на освещение цеха. Таблица 3.2 Затраты электроэнергии на выпуск продукции
Решение. Обозначим нормы затрат электроэнергии на изготовление продукции вида А, Б и затраты на освещение -
Из второго уравнения вычитаем первое и получаем: Для дальнейшего планирования энергопотребления можно использовать следующее выражение:
После подстановки в данное выражение планируемого выпуска продукции вида А (
-Опытный метод основан на определении норм путем опроса технологов, мастеров цеха или других опытных специалистов. Как видно из приведенных выше примеров, определение норм связано со сравнительно большими временными затратами (либо на проведение математических расчетов, либо на проведение наблюдений и экспериментов). В условиях единичного производства такие затраты зачастую являются нецелесообразными. Поэтому при планировании материальных затрат и затрат на оплату труда используются нормы установленные экспертным путем. Точность данных норм не столь высока, однако удается избежать временных затрат, связанных с определением величин норм с использованием математического аппарата.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

 , (2.26)
, (2.26) - темп роста, который находится из выражения:
- темп роста, который находится из выражения: , (2.27)
, (2.27) , (2.28)
, (2.28) . (2.29)
. (2.29) ;
; ;
; ;
;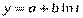 ;
; ;
;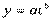 .
. .
. и
и  обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда:
обычно используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений динамического ряда: , (2.30)
, (2.30) и
и 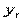 - расчетные и фактические значения;
- расчетные и фактические значения; - число наблюдений.
- число наблюдений. (2.31)
(2.31) или
или  (2.32)
(2.32)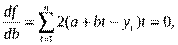
 (2.33)
(2.33) порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:
порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра. Так как прогнозируемые процессы носят вероятностный характер, то помимо точечного прогноза, как правило, определяют границы возможного изменения прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле: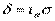 , (2.34)
, (2.34) - коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 2.4);
- коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 2.4);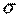 - среднеквадратическое отклонение от тренда,
- среднеквадратическое отклонение от тренда,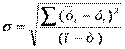 ; (2.35)
; (2.35) - число параметров аналитической зависимости.
- число параметров аналитической зависимости.

 ,
,  и
и  , имеет вид:
, имеет вид: (2.36)
(2.36)
 .
.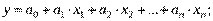
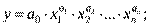
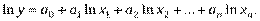
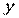 ) как функции цены единицы товара (
) как функции цены единицы товара ( ) и среднедушевого денежного дохода (
) и среднедушевого денежного дохода ( ). Например, для товаров длительного пользования часто используются следующие модели:
). Например, для товаров длительного пользования часто используются следующие модели: ;
; .
. ), а годовой объем производства – 200 шт. (
), а годовой объем производства – 200 шт. (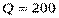 ), то трудоёмкость составит
), то трудоёмкость составит  часов. При использовании для изготовления изделий одних и тех же технологий величина нормы остаётся постоянной.
часов. При использовании для изготовления изделий одних и тех же технологий величина нормы остаётся постоянной. шт.
шт. руб. В том случае, когда хлеб не продается в день его завоза, магазин несёт убыток с каждой буханки:
руб. В том случае, когда хлеб не продается в день его завоза, магазин несёт убыток с каждой буханки:  руб. Если бы номинальная прибыль и потери, связанные с не реализацией хлеба были бы одинаковы, то ежедневная норма завоза хлеба была бы равна среднему объёму продаж за день, т.е. 135 буханок. Однако убыток, связанный с не реализацией превышает прибыль, получаемую в результате продажи буханки хлеба, а значит, норма завоза должна быть меньше 135 буханок.
руб. Если бы номинальная прибыль и потери, связанные с не реализацией хлеба были бы одинаковы, то ежедневная норма завоза хлеба была бы равна среднему объёму продаж за день, т.е. 135 буханок. Однако убыток, связанный с не реализацией превышает прибыль, получаемую в результате продажи буханки хлеба, а значит, норма завоза должна быть меньше 135 буханок. -вой буханки хлеба -
-вой буханки хлеба -  . Тогда ожидаемая прибыль, получаемая от реализации
. Тогда ожидаемая прибыль, получаемая от реализации 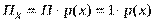 . (3.1)
. (3.1) -вой буханки хлеба:
-вой буханки хлеба: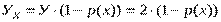 , (3.2)
, (3.2) - вероятность того, что
- вероятность того, что 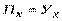 , или
, или  .
.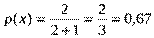 .
.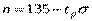 ,
, - коэффициент нормального распределения, зависящий от значения функции Лапласа –
- коэффициент нормального распределения, зависящий от значения функции Лапласа –  , при
, при 
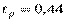 (приложение 1);
(приложение 1); - среднее квадратическое отклонение, для нашего случая:
- среднее квадратическое отклонение, для нашего случая:
 .
.


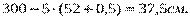
 , в зависимости от того в какой размерности установлена цена на материал. Однако проанализируем возможность комбинации различных вариантов распила прутка.
, в зависимости от того в какой размерности установлена цена на материал. Однако проанализируем возможность комбинации различных вариантов распила прутка. - доля прутков, разрезаемых 3-м способом. Количество заготовок вида А и Б, а также долю
- доля прутков, разрезаемых 3-м способом. Количество заготовок вида А и Б, а также долю  ;
; .
. ,
,  и
и  .
.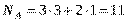 ,
, 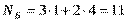 , т.е. из 10 прутков можно вырезать по 22 заготовки каждого вида, а это - 11 изделий.
, т.е. из 10 прутков можно вырезать по 22 заготовки каждого вида, а это - 11 изделий. м.пог/шт, или
м.пог/шт, или  кг/шт.
кг/шт. - доля прутков, разрезаемых 4-м способом, тогда:
- доля прутков, разрезаемых 4-м способом, тогда: ;
;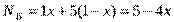 .
. ,
,  и
и  .
. ,
, 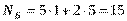 , т.е. из 14 прутков можно вырезать по 30 заготовок каждого вида и, соответственно, получить 15 изделий.
, т.е. из 14 прутков можно вырезать по 30 заготовок каждого вида и, соответственно, получить 15 изделий. м.пог/шт, или
м.пог/шт, или  кг/шт.
кг/шт. м.пог/шт, или 6,55 кг/шт).
м.пог/шт, или 6,55 кг/шт).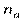 ,
,  и
и  , соответственно. Тогда по имеющимся данным за прошедшие месяцы (январь, февраль, март) можно составить следующую систему уравнений:
, соответственно. Тогда по имеющимся данным за прошедшие месяцы (январь, февраль, март) можно составить следующую систему уравнений: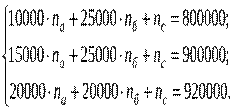
 отсюда норма затрат на изготовление изделия А -
отсюда норма затрат на изготовление изделия А -  кВтч. Вычитая из третьего уравнения второе, имеем:
кВтч. Вычитая из третьего уравнения второе, имеем:  , и
, и  кВтч. Для вычисления постоянных затрат на освещение цеха подставим полученные величины норм
кВтч. Для вычисления постоянных затрат на освещение цеха подставим полученные величины норм 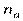 и
и  в первое уравнение:
в первое уравнение: 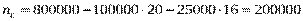 кВтч.
кВтч.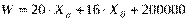 .
. ) и вида Б (
) и вида Б ( ) получим плановые затраты электроэнергии.
) получим плановые затраты электроэнергии.


