
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В.А. Воловоденко, Н.Л. Борщёва, О.В. МарухинаСодержание книги
Поиск на нашем сайте
В.А. Воловоденко, Н.Л. Борщёва, О.В. Марухина
ЭКОНОМЕТРИКА
Рекомендовано в качестве учебного пособия
Издательство Томского политехнического университета
УДК 51(075.8)
В 68
Воловоденко В.А. В 68 Эконометрика: учебное пособие / В.А. Воловоденко,
В пособии рассматриваются вопросы по основным разделам эконометрики: парная и множественная регрессия, системы эконометрических уравнений и временные ряды. Предназначено для студентов направления 521600 «Экономика» и специальностей 060500 «Бухгалтерский учет, анализ и аудит», 060700 «Национальная экономика».
УДК 51(075.8)
Рецензенты Доктор технических наук, профессор ТУСУРа Ю.П. Ехлаков
Кандидат технических наук, доцент кафедры КСУП ТУСУРа Н.Ю. Хабибулина
© Воловоденко В.А., Борщёва Н.Л., Марухина О.В., 2008 © Томский политехнический университет, 2008
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ. 3 ВВЕДЕНИЕ. 5 1. ОСНОВЫ СОВРЕМЕННОЙ ЭКОНОМЕТРИКИ.. 6 1.1. Определение эконометрики. 6 1.2. Структура эконометрики. 10 1.3. Нечисловые экономические величины.. 14 1.4. Эконометрические модели. 17 1.5. Применения эконометрических методов. 20 Контрольные вопросы.. 22 2. ПАРНАЯ РЕГРЕССИЯ.. 23 2.1. Спецификация модели. 23 2.2. Оценка параметров линейной регрессии. 25 2.3. Предпосылки МНК (условия Гаусса-Маркова) 29 2.4. Оценка существенности параметров линейной регрессии и корреляции 30 2.5. Нелинейные модели регрессии и их линеаризация. 35 Контрольные вопросы.. 43 3. ЛИНЕЙНАЯ МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ.. 44 3.1. Метод наименьших квадратов. 44 3.2. Оценка параметров линейного уравнения множественной регрессии 47 3.3. Частные уравнения регрессии. 53 3.4. Показатели качества регрессии. 56 3.5. Спецификация модели. 64 3.6. Линейные регрессионные модели с гетероскедастичными остатками 74 3.7. Линейные регрессионные модели с автокоррелированными остатками 80 3.8. Обобщенный метод наименьших квадратов (ОМНК) 86 3.9. Регрессионные модели с переменной структурой (фиктивные переменные) 91
Контрольные вопросы.. 98 4. СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.. 99 4.1. Структурная и приведенная формы модели. 100 4.2. Проблема идентификации. 101 4.3. Оценивание параметров структурной модели. Косвенный МНК, двухшаговый МНК, трехшаговый МНК.. 105 4.4. Применение систем эконометрических уравнений. 107 Контрольные вопросы.. 111 5. ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ 112 5.1. Характеристика временных рядов. 112 5.2. Динамические эконометрические модели. 128 Контрольные вопросы.. 136 Заключение. 137 Библиографический список.. 138
ВВЕДЕНИЕ Эконометрика исследует конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Как учебная дисциплина эконометрика изучается после прохождения курсов теории вероятностей и математической статистики и общей теории статистики (иногда - экономической статистики). Целью изучения учебной дисциплины «Эконометрика» является овладение современными эконометрическими методами анализа конкретных экономических данных на уровне, достаточном для использования в практической деятельности менеджера и менеджера-экономиста, инженера. Основные задачи курса - изучение современных эконометрических методов и моделей, в том числе методов прикладной статистики. Теоретическую базу эконометрики составляют математические дисциплины - общий курс (математический анализ, линейная алгебра), теория вероятностей и математическая статистика, дискретная математика, исследование операций; а также основы экономической теории и статистика (общая теория статистики, экономическая статистика). Настоящее учебное пособие соответствует Государственным образовательным стандартам по экономическим дисциплинам. Учебное пособие адресовано в первую очередь студентам дневных отделений экономических специальностей. Студенты-экономисты смогут изучить основы эконометрики и познакомиться с основными вопросами ее практического использования. Учебный материал в пособии условно разбит на пять частей. В первой части основное внимание уделено современной структуре эконометрики. Знакомство с ней необходимо для обоснованных суждений о возможностях применения эконометрических методов и моделей в экономических и технико-экономических исследованиях.
Во второй части рассмотрены модели парной регрессии (линейная и нелинейные модели). В третьей части достаточно подробно разбирается модель множественной линейной регрессии, обсуждаются проблемы гомоскедастичности и автокоррелированности остатков. Четвертая часть посвящена системам одновременных эконометрических уравнений. В пятой части рассматриваются модели временных рядов. Определение эконометрики Сначала необходимо выяснить, что обычно понимают под эконометрикой. Затем обсудим современное состояние эконометрики как научно-практической дисциплины. Эконометрика – это наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории, экономической статистики и экономических измерений, математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. Эконометрика как научная дисциплина зародилась и получила развитие на основе слияния экономической теории, математической экономики и экономической и математической статистики. По словам Р. Фриша: «… каждая из трех отправных точек – статистика, экономическая теория и математика - необходимое, но недостаточное условие для понимания количественных соотношений в современной экономической жизни. Это единство всех трех составляющих. Таким образом, эконометрика – это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов. Предметом эконометрики являются экономические явления. Но, в отличие от экономической теории, эконометрика делает упор на количественные, а не на качественные аспекты этих явлений. В эконометрике широко используется аппарат математической статистики, особенно при установлении связей между экономическими показателями. В то же время в экономике невозможно проведение управляемого эксперимента, и эконометристы используют свои собственные приемы анализа, которые в математической статистике не встречаются. Эконометрическое моделирование реальных социально-экономических процессов и систем обычно преследует два типа конечных прикладных целей (или одну из них): 1) прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы; 2) имитацию различных возможных сценариев социально-экономического развития анализируемой системы (многовариантные сценарные расчеты, ситуационное моделирование). При постановке задач эконометрического моделирования следует определить их иерархический уровень и профиль. Анализируемые задачи могут относиться к макро- (страна, межстрановой анализ), мезо- (регионы внутри страны) и микро- (предприятия, фирмы, семьи) уровням и быть направленными на решение вопросов различного профиля инвестиционной, финансовой или социальной политики, ценообразования, распределительных отношений и т. п.
Основные задачи эконометрики: 1. Построение эконометрических моделей, т. е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа (спецификация модели). 2. Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным (параметризация). 3. Проверка качества найденных параметров модели и самой модели в целом (верификация). 4. Использование построенных моделей для объяснения поведения экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики. Этапы эконометрического моделирования: 1. Постановочный этап: определение конечных целей моделирования, набора факторов и показателей. 2. Априорный этап: предмодельный анализ экономической сущности изучаемого явления. 3. Параметризация: собственно моделирование, т. е. выбор общего вида модели, состава и формы входящих в нее связей. 4. Информационный этап: сбор статистической информации. 5. Идентификация модели: статистический анализ модели и оценивание неизвестных параметров модели. 6. Верификация модели: сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.
Эконометрические методы - это прежде всего методы статистического анализа конкретных экономических данных, естественно, с помощью компьютеров. В нашей стране они пока сравнительно мало известны, хотя именно у нас наиболее мощная научная школа в области основы эконометрики – теории вероятностей. В настоящей главе дается общее представление о структуре и возможностях эконометрики, включая ее последние достижения. Эконометрический метод складывался в преодолении следующих трудностей, искажающих результаты применения классических статистических методов (сущность новых терминов будет раскрыта в дальнейшем): · асимметричности связей; · мультиколлинеарности связей; · эффекта гетероскедастичности; · автокорреляции; · ложной корреляции; · наличия лагов. Статистические (эконометрические) методы используются в зарубежных и отечественных экономических и технико-экономических исследованиях, работах по управлению (менеджменту). Применение прикладной статистики и других статистических методов дает заметный экономический эффект. Например, в США - не менее 20 миллиардов долларов ежегодно только в области статистического контроля качества. В 1988 г. затраты на статистический анализ данных в нашей стране оценивались в 2 миллиарда рублей ежегодно[1]. Следовательно, объем отечественного «рынка статистических и эконометрических услуг» был на порядок меньше, чем в США, что совпадает с оценками и по другим показателям, например, по числу специалистов.
Эконометрика (как учебный предмет) призвана вооружить экономиста, менеджера, инженера современным эконометрическим инструментарием, разработанным за последние 50-70 лет. Не владея эконометрикой, отечественный специалист - менеджер и инженер - оказывается неконкурентоспособным по сравнению с зарубежным. Во многих странах мира: Японии и США, Франции и Швейцарии, Перу и Ботсване и др. - статистическим методам обучают в средней школе, ЮНЕСКО постоянно проводят конференции по вопросам такого обучения[2]. Обсудим сложившуюся ситуацию, уделив основное внимание статистическим методам в экономических и технико-экономических исследованиях, т. е. эконометрике.
Эконометрика = экономика + метрика Действительно, термин «эконометрика» состоит из двух частей: «эконо-» - от «экономика» и «-метрика» - от «измерение». Эконометрика (в другом русско- и англоязычном варианте названия этой дисциплины - эконометрия) входит в обширное семейство дисциплин, посвященных измерениям и применению статистических методов в различных областях науки и практики. К этому семейству относятся, в частности, биометрика (или биометрия), технометрика, наукометрия, психометрика, хемометрика (наука об измерениях и применении статистических методов в химии). Особняком стоит социометрия - этот термин закрепился за статистическими методами анализа взаимоотношений в малых группах, т. е. за небольшой частью такой дисциплины, как статистический анализ в социологии. Эконометрика посвящена развитию и применению статистических методов в конкретной области науки и практики - в экономике, прежде всего, в теории и практике менеджмента. В мировой науке эконометрика занимает достойное место. Нобелевские премии по экономике получили эконометрики Ян Тильберген, Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо. В 2000 г. к ним добавились - Джеймс Хекман и Дэниель Мак-Фадден. Выпускается ряд научных журналов, полностью посвященных эконометрике, в том числе: · Journal of Econometrics (Швеция), · Econometric Reviews (США), · Econometrica (США), · Sankhya. Indian Journal of Statistics. Ser.D. Quantitative Economics (Индия), · Publications Econometriques (Франция). Рассмотрим современную структуру эконометрики. Знакомство с ней необходимо для обоснованных суждений о возможностях применения эконометрических методов и моделей в экономических и технико-экономических исследованиях. Структура эконометрики В эконометрике, как дисциплине на стыке экономики, включая менеджмент, и статистического анализа, естественно выделить три вида научной и прикладной деятельности (по степени специфичности методов, сопряженной с погруженностью в конкретные проблемы):
· (а) разработка и исследование эконометрических методов (методов прикладной статистики) с учетом специфики экономических данных; · (б) разработка и исследование эконометрических моделей в соответствии с конкретными потребностями экономической науки и практики; · (в) применение эконометрических методов и моделей для статистического анализа конкретных экономических данных. Кратко рассмотрим три только что выделенных вида научной и прикладной деятельности. По мере движения от первого к последнему виду научной и прикладной деятельности в эконометрике сужается широта области применения конкретного эконометрического метода, но при этом повышается его значение для анализа конкретной экономической ситуации. Если работам вида (а) соответствуют научные результаты, значимость которых оценивается по общеэконометрическим критериям, то для работ вида (в) основное - успешное решение задач конкретной области экономики. Работы вида (б) занимают промежуточное положение, поскольку, с одной стороны, теоретическое изучение эконометрических моделей может быть весьма сложным и математизированным, с дру- Прикладная статистика - другая область знаний, чем математическая статистика. Это четко проявляется и при преподавании. Курс математической статистики состоит в основном из доказательств теорем, как и соответствующие учебные пособия. В курсах прикладной статистики и эконометрики основное - методология анализа данных и алгоритмы расчетов, а теоремы приводятся как обоснования этих алгоритмов, доказательства же, как правило, опускаются (их можно найти в научной литературе). Внутренняя структура статистики как науки была выявлена и обоснована при создании в 1990 г. Всесоюзной статистической ассоциации[3]. Прикладная статистика - методическая дисциплина, являющаяся центром статистики. При применении к конкретным областям знаний и отраслям народного хозяйства получаем научно-практические дисциплины типа «статистика в промышленности», «статистика в медицине» и др. С этой точки зрения эконометрика - это «статистические методы в экономике». Математическая статистика играет роль математического фундамента для прикладной статистики. К настоящему времени, очевидно, четко выраженное размежевание этих двух научных направлений. Математическая статистика исходит из сформулированных в 1930-50 гг. постановок математических задач, происхождение которых связано с анализом статистических данных. В настоящее время исследования по математической статистике посвящены обобщению и дальнейшему математическому изучению этих задач. Термин «прикладная статистика» используется с 1960-х годов. Прикладная статистика нацелена на решение реальных задач. Поэтому в ней возникают новые постановки математических задач анализа статистических данных, развиваются и обосновываются новые методы. Обоснование часто проводится математическими методами, т. е. путем доказательства теорем. Большую роль играет методологическая составляющая - как именно ставить задачи, какие предположения принять с целью дальнейшего математического изучения. Велика роль современных информационных технологий. Статистические данные собираются и анализируются с незапамятных времен, современная математическая статистика как наука была создана, по общему мнению специалистов, сравнительно недавно - в первой половине ХХ в. Именно тогда были разработаны основные идеи и получены результаты, излагаемые ныне в учебных курсах математической статистики. После чего специалисты по математической статистике занялись внутриматематическими проблемами, а для теоретического обслуживания проблем практического анализа статистических данных стала формироваться новая дисциплина - прикладная статистика. В настоящее время статистическая обработка данных проводится, как правило, с помощью соответствующих программных продуктов. Разрыв между математической и прикладной статистикой проявляется, в частности, в том, что большинство методов, включенных в статистические пакеты программ (например, в заслуженные Statgraphics и SPSS или в более новую систему Statistica), даже не упоминается в учебниках по математической статистике. В результате специалист по математической статистике оказывается зачастую беспомощным при обработке реальных данных. Ситуация с внедрением современных статистических (эконометрических) методов на предприятиях и в организациях различных отраслей противоречива. К сожалению, при развале отечественной промышленности в 1990-е годы больше всего пострадали структуры, наиболее нуждающиеся в эконометрических методах - службы качества, надежности, центральные заводские лаборатории и др. Но толчок к развитию получили службы маркетинга и сбыта, сертификации, прогнозирования, инноваций и инвестиций, которым также полезны различные эконометрические методы, в частности, методы экспертных оценок.
Эконометрические модели Статистические и математические модели экономических явлений и процессов определяются спецификой той или иной области экономических исследований. Так, в экономике качества модели, на которых основаны статистические методы сертификации и управления качеством - модели статистического приемочного контроля, статистического контроля (статистического регулирования) технологических процессов (обычно с помощью контрольных карт Шухарта или кумулятивных контрольных карт), планирования экспериментов, оценки и контроля надежности и другие - используют как технические, так и экономические характеристики, а потому относятся к эконометрике, равно как и многие модели теории массового обслуживания (теории очередей). Экономический эффект только от использования статистического контроля в промышленности США оценивается как 0,8 % валового национального продукта (20 миллиардов долларов в год), что существенно больше, чем от любого иного экономико-математического или эконометрического метода. Ввиду важности статистических методов в стандартизации и управления качеством в СССР с начала 70-х годов разрабатывались государственные стандарты по статистическим методам в рассматриваемой области. По мнению ряда специалистов, из-за неграмотности разработчиков государственные стандарты содержали многочисленные ошибки. Для анализа ситуации в 1985 г. была организована рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам. В этот научный коллектив входили 66 научных работников и специалистов из различных отраслей народного хозяйства и вузов, в том числе более 20 докторов наук. Оказалось, что существенная часть стандартов по статистическим методам действительно содержала грубые ошибки. Основная часть ошибочных стандартов была отменена. Затем с целью исправления положения был организован Всесоюзный центр по статистическим методам и информатике (сейчас - Институт высоких статистических технологий и эконометрики МГТУ Наибольшее распространение получила система НАДИС (НАДежность и ИСпытания), созданная под руководством проф. О.И. Тескина (МГТУ им. Н.Э. Баумана). Важный раздел эконометрики - теория и практика экспертных оценок. Экспертные оценки используют для решения ряда экономических задач, например, выбора оптимального направления инвестиций или наилучшего образца определенного вида продукции для организации массового выпуска, или при прогнозировании развития экономической ситуации, или при распределении финансирования. Следовательно, используемые в теории экспертных оценок модели являются эконометрическими. Более известными в теоретических и учебных публикациях являются различные эконометрические модели, предназначенные для прогнозирования макроэкономических показателей. Это обычно модели весьма частного вида, имеющие целью прогнозирование многомерного временного ряда. Они представляют собой систему линейных зависимостей между прошлыми и настоящими значениями переменных. В таких задачах оценивают как структуру модели, т. е. вид зависимости между значениями известных координат вектора в прежние моменты времени и их значениями в прогнозируемый момент (т. е. проводят идентификацию модели), так и коэффициенты, входящие в эту зависимость. Структура такой модели - объект нечисловой природы, что и объясняет сложность соответствующей теории. Каждой области экономических исследований, связанной с анализом эмпирических данных, как правило, соответствуют свои эконометрические модели. Например, для моделирования процессов налогообложения с целью оценки результатов применения управляющих воздействий (например, изменения ставок налогов) на процессы налогообложения должен быть разработан комплекс соответствующих эконометрических моделей. Кроме системы уравнений, описывающей динамику системы налогообложения под влиянием общей экономической ситуации, управляющих воздействий и случайных отклонений, необходим блок экспертных оценок. Полезен блок статистического контроля, включающий как методы выборочного контроля правильности уплаты налогов (налогового аудита), так и блок выявления резких отклонений параметров, описывающих работу налоговых служб. Подходам к проблеме математического моделирования процессов налогообложения посвящены работы эконометристов Н.Ю. Ивановой, А.И. Орлова, их научные труды содержат также информацию о современных статистических (эконометрических) методах и экономико-математических моделях, в том числе имитационных. С помощью эконометрических методов следует оценивать различные величины и зависимости, используемые при построении имитационных моделей процессов налогообложения, в частности, функции распределения предприятий по различным параметрам налоговой базы. При анализе потоков платежей необходимо использовать эконометрические модели инфляционных процессов, поскольку без оценки индекса инфляции невозможно вычислить дисконт-функцию, а потому нельзя установить реальное соотношение авансовых и «итоговых» платежей. Прогнозирование сбора налогов может осуществляться с помощью системы временных рядов - на первом этапе по каждому одномерному параметру отдельно, а затем - с помощью некоторой линейной эконометрической системы уравнений, дающей возможность прогнозировать векторный параметр с учетом связей между координатами и лагов, т. е. влияния значений переменных в определенные прошлые моменты времени. Возможно, более полезными окажутся имитационные модели более общего вида, основанные на интенсивном использовании современной вычислительной техники. ПАРНАЯ РЕГРЕССИЯ Спецификация модели Регрессия представляет собой зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от функциональной зависимости, когда каждому значению независимой переменной х соответствует одно определенное значение величины y, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины y. В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии. Простая регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида:
где y – зависимая переменная (результативный признак); x – независимая, или объясняющая переменная (признак – фактор, или регрессор). Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида:
Любое эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Из всего круга факторов, влияющих на результативный признак, необходимо выделить наибольшие, существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Например, выдвигается гипотеза о том, что величина спроса y на товар находится в обратной зависимости от цены x, т. е. Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как закономерность лишь в среднем по совокупности наблюдений. (Например, если зависимость спроса y от цены x: В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи. В каждом отдельном случае величина y складывается из двух слагаемых:
где Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее порождают 3 источника: спецификация модели, выборочный характер исходных данных и ошибки измерения. Например, зависимость спроса от цены точнее следует записывать так: В данном случае слева записано просто y, что означает фактическое значение, а не Ошибки спецификации. Это, прежде всего, неправильно выбранная форма модели. В частности, зависимость спроса от цены может быть выражена линейно
но возможны и другие соотношения, например:
Ошибки спецификации тем меньше, чем в большей мере теоретические значения признака подходят к фактическим данным y. К ошибкам спецификации относится также недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Например, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения. Ошибки выборки. Исследователь при установлении связи между признаками имеет дело с выборочными данными. При изучении экономических процессов данные в исходной совокупности часто являются неоднородными. В этом случае уравнение регрессии не имеет практического смысла. Поэтому для получения хорошего результата из выборки исключают единицы с аномальными значениями исследуемых признаков. Ошибки измерения. Представляют наибольшую опасность в практическом использовании методов регрессии. Ошибки спецификации можно уменьшить, изменяя форму модели, ошибки выборки – увеличивая объем исходных данных, ошибки измерения сводят на нет все усилия по количественной оценке связи между признаками. Например, статистическое измерение дохода на душу населения может иметь ошибку в результате наличия сокрытых доходов. Другой пример: органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. В эконометрических исследованиях предполагается, что ошибки измерения сведены к минимуму. Поэтому основное внимание уделяется ошибкам спецификации модели. В парной регрессии выбор вида математической функции (1) может быть осуществлен тремя методами: графическим, аналитическим и экпериментальным. Метод наименьших квадратов На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии рассматривается множественная регрессия
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и в ряде других вопросов экономики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основной целью множественной регрессии является построение модели с большим числом факторов, а также определение влияния каждого фактора в отдельности и совокупного их воздействия на моделируемый показатель. Множественный регрессионный анализ является развитием парного регрессионного анализа в случаях, когда зависимая переменная связана более чем с одной независимой переменной. Большая часть анализа является непосредственным расширением парной регрессионной модели, но здесь также появляются и некоторые новые проблемы, из которых следует выделить две. Первая проблема касается исследования влияния конкретной независимой переменной на зависимую переменную, а также разграничения её воздействия и воздействий других независимых переменных. Второй важной проблемой является спецификация модели, которая состоит в том, что необходимо ответить на вопрос, какие факторы следует включить в регрессию (1), а какие – исключить из неё. В дальнейшем изложение общих вопросов множественного регрессионного анализа будем вести, разграничивая эти проблемы. Поэтому вначале будем полагать, что спецификация модели правильна. Самой употребляемой и наиболее простой из моделей множественной регрессии является линейная модель множественной регрессии:
По математическому смыслу коэффициенты
Параметр α´ называется свободным членом и определяет значение y в случае, когда все объясняющие переменные равны нулю. Но, как и в случае парной регрессии, факторы по своему экономическому содержанию часто не могут принимать нулевых значений, и значение свободного члена не имеет экономического смысла. При этом, в отличие от парной регрессии, значение каждого регрессионного коэффициента Отметим, что наиболее просто можно определять оценки параметров Получение оценок параметров Самым распространенным методом решения этой задачи является метод наименьших квадратов (МНК). Его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной y от её значений Поскольку параметры
Здесь
Пусть имеется n наблюдений объясняющих переменных и соответствующих им значений результативного признака:
Для однозначного определения значений параметров уравнения (4) объем выборки n должен быть не мень
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.84 (0.019 с.) |

 ББК 22.1
ББК 22.1 © Оформление. Издательство Томского
© Оформление. Издательство Томского 
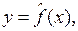
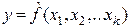 .
.
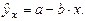
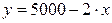 означает, что с ростом цены на 1 ден.ед. спрос в среднем уменьшается на 2 ден. ед.).
означает, что с ростом цены на 1 ден.ед. спрос в среднем уменьшается на 2 ден. ед.).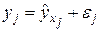 ,
,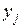 - фактическое значение результативного признака;
- фактическое значение результативного признака; 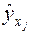 - значение признака, найденное из математической функции связи y и x, т. е. из уравнения регрессии;
- значение признака, найденное из математической функции связи y и x, т. е. из уравнения регрессии; 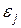 - случайная величина, характеризующая отклонение реального значения признака от найденного по уравнению регрессии.
- случайная величина, характеризующая отклонение реального значения признака от найденного по уравнению регрессии.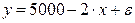 .
.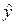 , отвечающее значению, рассчитанному по уравнению регрессии.
, отвечающее значению, рассчитанному по уравнению регрессии. ,
,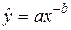 ,
, 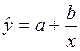 ,
,  .
. . (1)
. (1)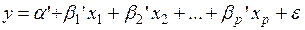 . (2)
. (2)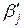 в уравнении (2) равны частным производным результативного признака y по соответствующим факторам:
в уравнении (2) равны частным производным результативного признака y по соответствующим факторам: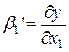 ,
,  ,…,
,…,  .
.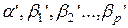 уравнения регрессии (2) – одна из важнейших задач множественного регрессионного анализа.
уравнения регрессии (2) – одна из важнейших задач множественного регрессионного анализа.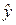 , получаемых по уравнению регрессии.
, получаемых по уравнению регрессии. . (3)
. (3)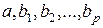 – оценки теоретических значений
– оценки теоретических значений 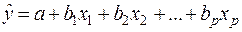 . (4)
. (4) . (5)
. (5)


