
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели качества подбора моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным. Для оценки качества модели регрессии используются специальные показатели. Качество линейной модели парной регрессии характеризуется с помощью следующих показателей: 1) парной линейный коэффициент корреляции, который рассчитывается по формуле:
G(y) – среднеквадратическое отклонение зависимой переменной. Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии 2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации. Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий. Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии: G2(y)=σ2(y)+δ2(y), где G2(y) – это общая дисперсия зависимой переменной; σ2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле: 1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi: 2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции: 3) показатель 4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE): Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной. Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле: 5) показатель средней ошибки аппроксимации рассчитывается по формуле:
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 889; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.242 (0.008 с.) |

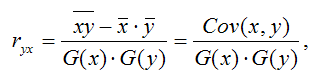 где G(x) – среднеквадратическое отклонение независимой переменной;
где G(x) – среднеквадратическое отклонение независимой переменной; по формуле:
по формуле: 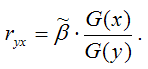 Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу. δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
δ2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле: 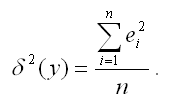 С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии: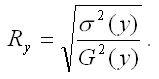 Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.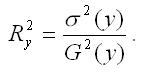 Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;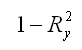 характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;
характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;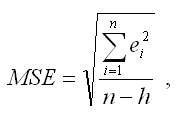 где h– это количество параметров, входящих в модель регрессии.
где h– это количество параметров, входящих в модель регрессии.
 Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.


