
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и метод эконометрики(Э). Этапы эконометрического исследования(ЭИ)Содержание книги
Поиск на нашем сайте Э. как наука расположена на стыке эк-ки, стат-ки. и мат-ки Предмет- колич выражение взаимосвязей эк явлений и процессов. Э. устан-ет и исследует колич закон-сти в эк-ке, используя понятия и методы теории вероятности и мат стат-ки. Закон-сти в эк-ке выражаются в виде связей и зависимостей эк показателей. Если причинно-следственными связями в эк-ке занимается эк. теория, то моделированием этих связей – Э.. Изучение эк. взаимосвязей осложнено тем, что они не являются строгими, функциональными зависимостями. 1. всегда очень трудно выявить все основные факторы, влияющую на данную переменную. 2. многие такие взаимодействия являются случайными, то есть содержат случайную составляющую. 3.экономисты располагают ограниченным набором данных стат наблюдений, к-ые содержат различные ошибки. Мат статистика и ее применение в экономике – Э. - позволяют строить эк модели и оценивать их параметры, что служит основой для эк анализа и прогнозирования, создавая возможность для принятия обоснованных эк решений. Э.: - это наука, связанная с эмпир выводом эк законов, т.е. мы используем данные эмпир наблюдений, чтобы получить колич зависимости эк переменных. Метод –система методов: корреляционный, регрессионный, проверка стат гипотез, дисперсионный, аналит выравнивание рядов динамики т.д. Этапы ЭИ: 1.Постановка проблемы (качеств. анализ связей эк. переменных – выделение зависимых (yi) и независимых переменных (xik)); А)Формулируются предмет и цели иссл-ния. Б)выделяются структурные или функциональные элементы, соответст. данной цели, выявляются наиболее важные качеств хар-ки этих элементов. В)Словесно, качественно описываются взаимосвязи между элементами модели. 2.Получение данных, анализ их качества; 3.Спецификация модели (форма связи между yi и xik);(вводятся символ. обозначения для учитываемых хар-тик эк. объекта и формализуются, насколько возможно, взаимосвязи между ними. Т.е. формулируется мат. модель) 4.Оценка параметров модели (опред-тся значения неизвестных одним из допустимых в каждом конкр случае методов, проверяется кач-во найденных оценок, т.е. вычисляется вер-сть того, насколько верно определены параметры, их значимость, а также соотв-вие модели эмпир. данным и теор. предпосылкам.Анализ осущ-тся по схеме проверки стат. гипотез. Совершенствуется не только форма модели, но и уточняется состав объясняющих ее переменных (н-р, спрос на товар определяется не только его ценой, но и другими факторами, н-р, располагаемым доходом). 5.Интерпретация рез-тов. (проводятся расчеты по мат. модели и анализ полученного решения. Если модель удовлетворяет требованиям кач-ва, то она м. б. исп-на для прогноз-ния, либо для анализа внутр. механизма исследуемых процессов). 41. Ковариация(ковр.), корреляция(коррел.) случайной величины.Св-ва коэффициента коррел. (КК) Взаимосвязь переменных х и у м.б. выражена одним числом. Показателями взаимосвязи переменных являются их ковариация и корреляция. Ковариация определяется по одной из формул: Устойчивой хар-кой взаимосвязи, т.е. не зависящей от масштаба переменных, явл-тся КК. В случае парной линейной зависимости переменных он определяется по формуле: 1. КК может принимать значения в интервале от -1 до +1 и равен +1 или -1 <=> когда все точки диаграммы лежат на прямой линии, т. е. в этом случае имеем функциональную зависимость. 2. Линейные преобразования, сводящиеся к изменению масштаба или начала отсчета случайных величин Х и У, не изменяют значения КК: 3. КК между независимыми случайными величинами Х и Y равен нулю. Обратное утверждение неверно, т. е. из равенства нулю КК не следует независимость случайных величин Х и Y. Если r(X,Y) = 0, то Х и Y называются некоррелированными. Только в одном случае некоррелированность случайных величин влечет их независимость. Это имеет место, если Х и Y распределены по нормальному закону. 42. Классическая парная линейная модель регрессии. Понятие выборочного уравнения регрессии. КК показывает, что две переменные связаны друг с другом, однако он не дает представления о том, каким образом они связаны. Рассмотрим более подробно те случаи, для которых мы предполагаем, что одна переменная зависит от другой.Не следует ожидать получения точного соотношения между какими-либо двумя эк показателями, за исключением тех случаев, когда оно существует по определению. В учебниках по экономической теории эта проблема обычно решается путем приведения соотношения, как если бы оно было точным, и предупреждения читателя о том, что это аппроксимация. В стат анализе факт неточности соотношения признается путем явного включения в него случайного фактора, описываемого случайным остаточным членом. Начнем с рассмотрения простейшей модели: y=a +bx+u (2.1) Величина у, рассматриваемая как зависимая переменная, состоит из двух составляющих: 1) неслучайной составляющейa + bx, где x выступает как объясняющая (или независимая) переменная, а постоянные величины a и b — как параметры уравнения; 2) случайного члена и.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 Cov (x, y) =
Cov (x, y) =  Величина показателя ковариации зависит от масштаба переменных, поэтому не является устойчивой хар-кой взаимосвязи и не подлежит смысловой интерпретации. Знак показателя ковар. указывает на направление связи: положит величина говорит, что связь прямая, а отрицат – об обратной связи.
Величина показателя ковариации зависит от масштаба переменных, поэтому не является устойчивой хар-кой взаимосвязи и не подлежит смысловой интерпретации. Знак показателя ковар. указывает на направление связи: положит величина говорит, что связь прямая, а отрицат – об обратной связи.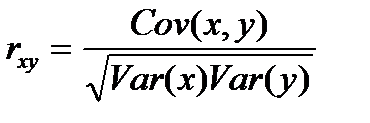 , где Var(х)=
, где Var(х)=  (х -
(х -  и Var(у) аналогично. Коэф-т парной корреляции r имеет мах значение, равное 1, к-рое получается при строгой линейной положит зависимости между выборочными значениями х и у. Аналогично r принимает мин значение -1, когда сущ. Линейная отрицат. Зависимость. Величина r=0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Промежуточные значения КК интерпретируются: 0-0,3 –слабая связь; 0,3-0,5-умеренная, 0,5-0,7 –средняя, 0,7-1 сильная или тесная зависимость. Если на зависимую переменную у параллельно с фактором х оказывает влияние еще фактор z, то коэф-нт парной корреляции между у и х может увеличивать или уменьшать действительную силу связи между ними. В таких случаях частный коэффициент корреляции явл-тся более точной мерой зависимости. Его величина:
и Var(у) аналогично. Коэф-т парной корреляции r имеет мах значение, равное 1, к-рое получается при строгой линейной положит зависимости между выборочными значениями х и у. Аналогично r принимает мин значение -1, когда сущ. Линейная отрицат. Зависимость. Величина r=0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Промежуточные значения КК интерпретируются: 0-0,3 –слабая связь; 0,3-0,5-умеренная, 0,5-0,7 –средняя, 0,7-1 сильная или тесная зависимость. Если на зависимую переменную у параллельно с фактором х оказывает влияние еще фактор z, то коэф-нт парной корреляции между у и х может увеличивать или уменьшать действительную силу связи между ними. В таких случаях частный коэффициент корреляции явл-тся более точной мерой зависимости. Его величина:  где rху.я - коэфф частной коррел между х и у в случае постоянства воздействия величины z, а rху, rxz и ryz - обычные коэфф-ты коррел между х и у, между х и z, между у и z соответственно. Если х,у –независимы, то cov(x,y)=0, r=0. Если х или у =const, то cov(x,y)=0. Если у=а+в, то cov(x,y)= cov(x,а)+ cov(x,в). Если у=k*c, k= const, то cov(x,y)=kcov(x,с). Св-ва КК:
где rху.я - коэфф частной коррел между х и у в случае постоянства воздействия величины z, а rху, rxz и ryz - обычные коэфф-ты коррел между х и у, между х и z, между у и z соответственно. Если х,у –независимы, то cov(x,y)=0, r=0. Если х или у =const, то cov(x,y)=0. Если у=а+в, то cov(x,y)= cov(x,а)+ cov(x,в). Если у=k*c, k= const, то cov(x,y)=kcov(x,с). Св-ва КК:
 На рис. показано, как комбинация этих двух составляющих определяет величину у. Показатели х1, х2, х3, х4 - это четыре гипотетических значения объясняющей переменной. Если бы соотношение между у и х было точным, то соответствующие значения у были бы представлены точками Q1, Q2, Q3, Q4 на прямой. Наличие случайного члена приводит к тому, что в действительности значение у получается другим. Предполагалось, что случайный член возмущения положителен в 1ом и 4ом наблюдениях и отрицателен в двух других. Поэтому если отметить на графике реальные значения у при соответствующих значениях х, то мы получим точки P1, P2, P3, P4. Точки Р — это единственные точки, отражающие реальные значения переменных на рис. Фактические значения a и b и, следовательно, положения точек Q неизвестны, так же как и фактические значения случайного члена. Задача регрессионного анализа состоит в получении оценок a и b и, следовательно, в определении положения прямой по точкам Р. Очевидно, что чем меньше значения и, тем легче эта задача. Действительно, если бы случайный член отсутствовал вовсе, то точки Р совпали бы с точками Q и точно показали бы положение прямой. В этом случае достаточно было бы просто построить эту прямую и определить значения a и b. Почему же существует случайный член?1. Невключение объясняющих переменных. Соотношение между у и х почти наверняка является очень большим упрощением. В действительности существуют другие факторы, влияющие на у, которые не учтены в формуле (2.1). Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой. В результате мы получаем то, что обозначено как и. Если бы мы точно знали, какие переменные присутствуют здесь, и имели возможность точно их измерить, то могли бы включить их в уравнение и исключить соответствующий элемент из случайного члена..2. Агрегирование переменных. Во многих случаях рассматриваемая зависимость — это попытка объединить вместе некоторое число микроэк соотношений. Например, функция суммарного потребления — это попытка общего выражения совокупности решений отдельных индивидов о расходах. Так как отдельные соотношения, вероятно, имеют разные параметры, любая попытка определить соотношение между совокупными расходами и доходом является лишь аппроксимацией. Наблюдаемое расхождение при этом приписывается наличию случайного члена.3. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Здесь можно привести один из многих возможных примеров. Если зависимость относится к данным о временном ряде, то значение у может зависеть не от фактического значения х, а от значения, которое ожидалось в предыдущем периоде. Если ожидаемое и фактическое значения тесно связаны, то будет казаться, что между у и х существует зависимость, но это будет лишь аппроксимация. Расхождение вновь будет связано с наличием случайного члена.4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Безусловно, надо постараться избежать возникновения этой проблемы, используя подходящую мат формулу, но любая самая изощренная формула является лишь приближением, и существующее расхождение вносит вклад в остаточный член.5. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить вклад в остаточный член.Остаточный член является суммарным проявлением всех этих факторов. Очевидно, что если бы нас интересовало только измерение влияния х на у, то было бы значительно удобнее, если бы остаточного члена не было. Если бы он отсутствовал, мы бы знали, что любое изменение у от наблюдения к наблюдению вызвано изменением х, и смогли бы точно вычислить b. Однако в действительности каждое изменение у отчасти вызвано изменением и, и это значительно усложняет жизнь.
На рис. показано, как комбинация этих двух составляющих определяет величину у. Показатели х1, х2, х3, х4 - это четыре гипотетических значения объясняющей переменной. Если бы соотношение между у и х было точным, то соответствующие значения у были бы представлены точками Q1, Q2, Q3, Q4 на прямой. Наличие случайного члена приводит к тому, что в действительности значение у получается другим. Предполагалось, что случайный член возмущения положителен в 1ом и 4ом наблюдениях и отрицателен в двух других. Поэтому если отметить на графике реальные значения у при соответствующих значениях х, то мы получим точки P1, P2, P3, P4. Точки Р — это единственные точки, отражающие реальные значения переменных на рис. Фактические значения a и b и, следовательно, положения точек Q неизвестны, так же как и фактические значения случайного члена. Задача регрессионного анализа состоит в получении оценок a и b и, следовательно, в определении положения прямой по точкам Р. Очевидно, что чем меньше значения и, тем легче эта задача. Действительно, если бы случайный член отсутствовал вовсе, то точки Р совпали бы с точками Q и точно показали бы положение прямой. В этом случае достаточно было бы просто построить эту прямую и определить значения a и b. Почему же существует случайный член?1. Невключение объясняющих переменных. Соотношение между у и х почти наверняка является очень большим упрощением. В действительности существуют другие факторы, влияющие на у, которые не учтены в формуле (2.1). Влияние этих факторов приводит к тому, что наблюдаемые точки лежат вне прямой. В результате мы получаем то, что обозначено как и. Если бы мы точно знали, какие переменные присутствуют здесь, и имели возможность точно их измерить, то могли бы включить их в уравнение и исключить соответствующий элемент из случайного члена..2. Агрегирование переменных. Во многих случаях рассматриваемая зависимость — это попытка объединить вместе некоторое число микроэк соотношений. Например, функция суммарного потребления — это попытка общего выражения совокупности решений отдельных индивидов о расходах. Так как отдельные соотношения, вероятно, имеют разные параметры, любая попытка определить соотношение между совокупными расходами и доходом является лишь аппроксимацией. Наблюдаемое расхождение при этом приписывается наличию случайного члена.3. Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Здесь можно привести один из многих возможных примеров. Если зависимость относится к данным о временном ряде, то значение у может зависеть не от фактического значения х, а от значения, которое ожидалось в предыдущем периоде. Если ожидаемое и фактическое значения тесно связаны, то будет казаться, что между у и х существует зависимость, но это будет лишь аппроксимация. Расхождение вновь будет связано с наличием случайного члена.4. Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Безусловно, надо постараться избежать возникновения этой проблемы, используя подходящую мат формулу, но любая самая изощренная формула является лишь приближением, и существующее расхождение вносит вклад в остаточный член.5. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить вклад в остаточный член.Остаточный член является суммарным проявлением всех этих факторов. Очевидно, что если бы нас интересовало только измерение влияния х на у, то было бы значительно удобнее, если бы остаточного члена не было. Если бы он отсутствовал, мы бы знали, что любое изменение у от наблюдения к наблюдению вызвано изменением х, и смогли бы точно вычислить b. Однако в действительности каждое изменение у отчасти вызвано изменением и, и это значительно усложняет жизнь.


