
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уровень значимости критерия проверки гипотез характеризуетСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найти дисперсию вариантов: 0,00017; 0,00015; 0,00013; 0,00016; 0,00014 2*10-10
Дано: P(A) = 0,8; P(B) = 0,2; P(A\B) = 0,4. Найти вероятность события B, если событие A произошло 0,1
На пяти карточках написаны буквы А, М, У, М, С. Вероятность того, что выбранные в последовательном порядке составят слова "сумма", равна...
Тело движется прямолинейно со скоростью
Вычислить определенный интеграл
Прибор для измерения расстояний имеет среднее квадратическое случайных ошибок =0,1м. найти доверительный интервал для оценки истинного расстояния с надежностью 0,97, если произведено 4 измерения: 9,8м; 10,1м; 10,2м; 10,1м. Табличные значения функции Лапласа: Ф(0,97)=0,334; Ф(2,17)=0,485 (9,94; 10,16)м Верно
Вычислить объем тела, образованного вращением вокруг оси ох криволинейной трапеции, ограниченной гиперболой xy = 4, прямыми x=1 и x=4 12п
Какие из следующих утверждений являются верными? 1. Если события А и В независимы, то 3,4,5,6,7 Дано: P(A) = 0,08; P(B) = 0,12; P(A+B) = 0,1. Найти вероятность совместного появления А и В. 0,1
На контрольных испытаниях 17 осветительных ламп были определены: средняя продолжительность работы лампы В урне 3 белых и 3 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,6 Случайная величина распределена по нормальному закону с параметром 1,96
Если статисческий критерий попал в область принятия решений, то нулевая гипотеза не противоречит опытным данным В урне 2 белых и 4 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,8 В урне 2 белых и 4 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян белый шар. 0,2 Вычислить интеграл: Наблюдаемое значение критерия Пирсона можно найти по формуле х В группе спортсменов 20 лыжников и 10 бегунов. Вероятность выполнить квалификационную норму равна для лыжника 0,9, для бегуна 0,75. Найти вероятность того, что спортсмен, вызванный наудачу, выполнит норму. 0,850 Определите закон распределения, найдите
Найдите с надежностью 2,58
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают Найти неопределенный интеграл:
Интеграл
Точка движется по прямой так, что ее скорость в момент времени t равна
Вероятность того, что спортсмен победит в первом виде многоборья, равна 0,9, а вероятность того, что он победит во втором виде многоборья, равна 0,7. Какова вероятность, что спортсмен победит и в первом и во втором видах многоборья(считать, что победы в равных видах многоборья - независимые события). 0,63
Вычислить неопределенный интеграл
Два стрелка независимо друг от друга стреляют в одну и ту же цель и делают по одному выстрелу. Вероятность попадания в цель первого стрелка 0,6, второго 0,7. Какова вероятность того, что оба стрелка попадут в цель? 0,42
Имеются выборочные данные о дневном сборе урожая:
Вычислить выборочную среднюю. 35,0375
В урне 2 белых и 3 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,75 В урне 2 белых и 3 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян белый шар. 0,25 Вероятность появления события в каждом испытании равна 0,25 вероятность того, что событие появится ровно 70 раз в 243 испытаниях равна... 0,0231
Вычислить площадь фигуры, заключенной между параболами
Бросаются две игральные кости. Вероятность того, что на обеих костях выпадут шестерки, равна...
Дана выборка объема n. Если каждый элемент выборки уменьшить в 4 раза, то выборочное среднее х... Уменьшится в 4 раза
Пусть задана функция
В электрическую цепь последовательно включены 2 элемента, работающих независимо один от другого. Вероятности отказов первого и второго соответственно равны 0,1 и 0,15. Найти вероятность того, что тока в цепи не будет. 0,235
Значение определенного интеграла 8 Вычислить объем тела, образованного вращением фигуры, ограниченной линиями:
При заданном уровне значимости статистического критерия, критическую область выбирают так, чтобы: а)вероятность ошибки 1-го рода была минимальна б)вероятность ошибки 2-го рода была минимальна в)вероятность ошибок 1-го и 2-го рода была минимальна г)надежность критерия была максимальна б
Дано: P(A) = 0,5; P(B) = 0,8; P(A\B) = 0,2. Найти вероятность события B, если событие A произошло. 0,32
Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено ровно 3 изделия.
Выборочная совокупность задана таблицей распределения...
Найти среднее число работающих на предприятии.
Дано: P(A) = 0,3; P(B) = 0,8; P(A\B) = 0,15. Найти вероятность события B, если событие A произошло. 0,4
На скамью случайным образом рассаживаются 5 человек, какова вероятность, что Саша и Маша окажутся рядом? 0,4 Доверительная вероятность это вероятность, с которой доверительный интервал накрывает истинное значение параметра
Дано: P(A) = 0,05; P(B) = 0,1; P(A+B) = 0,12. Найти вероятность совместного появления А и В. 0,03 Дано: P(A) = 0,5; P(B) = 0,3; P(A+B) = 0,68. Найти вероятность совместного появления А и В. 0,12 Нулевой называют проверяемую гипотезу Вероятности появления каждого из двух независимых событий равны – 0,8 и 0,7. Найти вероятность появления только одного из этих событий. 0,38 Вероятность того, что спортсмен займет в соревнованиях первое место, равна 0,3, вероятность занять второе место, равна 0,5, и вероятность занять третье место – 0,1, Вероятность того, что спортсмен займет хотя бы второе место, равна... 0,8
Число бракованных деталей Х в партии деталей является случайной величиной, распределённой по закону Пуассона. По данным таблицы найти методом моментов оценку параметра распределения Пуассона
0,51
В урне 3 белых и 4 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,67
Найти общую среднюю на основе выборки:
3,6 В урне 3 белых и 2 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян белый шар. 0,5 В урне 3 белых и 2 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,5 Вычислите площадь фигуры, ограниченной кривой Из генералной совокупности извлечена выборка объема n=50:
Тогда
Вычислить площадь фигуры, заключенной между линиями: Дифференциал функции
Наблюдаемым значением критерия проверки гипотез называют значение критерия, найденное по выборкам Распределение задано интервальным рядом:...
Найти среднее время на обработку одной детали. Отправляя письмо, Вы забыли последнюю цифру в индексе адреса и написали ее наугад. Какова вероятность того, что Вы написали нужную цифру?
Вычислить неопределенный интеграл
Дано: P(A) = 0,3; P(B) = 0,8; P(A\B) = 0,15. Найти вероятность события B, если событие A произошло. 0,4 Выборочная доля, как оценка генеральной доли, является: а)состоятельной б)несмещённой в)эффективной г)смещённой д)точной а,б,в Выборочная дисперсия, как оценка генеральной дисперсии, является: а)состоятельной б)несмещённой в)асимптотически эффективной г)смещённой д)точной а,в,г В урне 4 белых и 4 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,57
Найдите дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной равномерно в интервале
Дано: P(A) = 0,4; P(B) = 0,1; P(A+B) = 0,48. Найти вероятность совместного появления А и В. 0,02 Тело движется прямолинейно со скоростью 48м
Две лампы соединены параллельно. Вероятность того, что в течение некоторого времени перегорит первая лампа, равна 0,6, а для второй лампы эта вероятность равна 0,4. Какова вероятность того, что за рассматриваемое время произойдет разрыв в цепи? Считать, что выход из строя каждой из ламп - независимые события 0,24 Найдите множество первообразных для функции
Исправленная выборочная дисперсия, как оценка генеральной дисперсии, является: а)состоятельной б)несмещённой в)асимптотически эффективной г)смещённой д)точной а,б,в Для выборки объема В урне 4 белых и 2 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,4 Дано: P(A) = 0,2; P(B) = 0,3; P(A+B) = 0,35. Найти вероятность совместного появления А и В. 0,15
Вычислить площадь фигуры, ограниченной линиями:
Известно, что Х имеет равномерное распределение. По выборке большого объёма найдены 40 и 74,6 Если основная гипотеза имеет вид
Вероятность попадания по движущейся мишени равна 0,7. Какова вероятность того, что из 20 выстрелов 15 окажутся удачными. 0,173
Дано: P(A) = 0,15; P(B) = 0,45; P(A+B) = 0,5. Найти вероятность совместного появления А и В. 0,1 Вычислить неопределенный интеграл
Найдите 0,75 Вычислить площадь фигуры, заключенной между параболой Вычислить площадь фигуры, заключенной между параболой
Известно, что
Вычислить объем тела, образованного вращением фигуры, ограниченной линиями: 16
0,5 Вероятность появления события А в отдельном испытании 0,5467
1 Найти медиану
Точка В симетрична с А(4;-1) относительно биссектрисы первого координатного угла, найти длину АВ
Под каким углом к оси 0Х наклонена касательная к кривой
Найти неопределенный интеграл
Дано: P(A) = 0,25; P(B) = 0,75; P(A\B) = 0,15. Найти вероятность события B, если событие A произошло. 0,45 Вычислить площадь фигуры, ограниченной линиями: Найдите среднее квадратическое отклонение, заданной функцией распределения
Вычислить площадь фигуры, заключенной между параболой
В урне три черных шара и шесть белых. Найдите вероятность того, что из 5 наугад выбранных шаров ровно 3 белых.
Найти доверительный интервал для оценки с надежностью 0,95 параметра (6,08; 13,92)
Найдите площадь фигуры, ограниченной линиями:
Найдите площадь фигуры, ограниченной линиями:
Набирая номер телефона, абонент забыл две последние цифры и помнил лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?
Пусть функция имеет вид
Найти первообразную функции
В группе из 30 учеников на контрольной работе 6 учеников получили " 5 ", 10 учеников " 4 ", 9 учеников " 3 ". Какова вероятность того, что 3 ученика, вызванных к доске, имеют неудовлетворительные оценки по контрольной работе?
Интервальной оценкой параметра числовой интервал, который с заданной вероятностью накрывает
Какова вероятность того, что последняя цифра номера проезжающей машины является нечетной или равна четырем?
Бросаются две игральные кости. Вероятность того, на обеих костях окажется по одинаковому числу очков, равна...
При проверке гипотезы о нормальном законе распределения по критерию Пирсона теоретические частоты находят по формуле n В урне 3 белых и 5 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,71 Вычислить площадь фигуры ограниченную линиями
Найти первообразную функции
В урне 4 белых и 3 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,5 Вычислить неопределенный интеграл Бросаются две игральные кости. Вероятность того, выпадут разные числа очков, равна...
Вероятности попадания в цель при стрельбе из двух орудий равны 0,7 и 0,9. Найдите вероятность хотя бы одного попадания при одном залпе из обоих орудий. 0,97 Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях - четная.
Число семян сорняков в пробе зерна является случайной величиной, распределённой по закону Пуассона. По данным таблицы найти методом моментов оценку параметра распределения Пуассона 0,88 Из генеральной совокупности извлечена выборка объема Вычислить интеграл: п
Вычислите предел функции lim(1+X)^2/x-1 e^2 Найти доверительный интервал для оценки с надежностью 0,95 параметра нормально распределенной величины Х, если по выборке объёма n=49 вычислена выборочная средняя =10..Генеральное среднее квадратическое отклонение =14. Табличные значения функции Лапласа: Ф(0,95)=0,329; Ф(1,96)=0,475 ( 6,08; 13,92) Тело движется прямолинейно со скоростью v(t)=2t^3+1Найти путь, пройденный телом за промежуток времени от t=1 до t=3 42m Найдите с надежностью Y ширину доверительного интервала для генеральной средней, если o=3.n=36.y=0.99 2.58 Найдите алгебраическое дополнение элемента A23[1 2 5] [3 -4 7] [-3 12 -15] -18
Определить расстояние между двумя точками А(3;8) и В(-5;14) 10 В урне 4 белых и 4 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян черный шар. 0,57 Найдите сумму произведений элементов 3-й строки данного определителя на алгебраические дополнения соответствующих элементов 2-й строки 3 17 -5 10 7 2 4 -1 5 0 Вычислите предел функции LIM 3x^3-1/6x^3+X-2 1/2 Вычислить площадь фигуры ограниченную линиями y=e^x y=0 x=0 x=2 е^2-1 Найдите математическое ожидание, заданной функцией распределенияF(x) 0при x<0.x-0.25х^2при xtisti[0.2] 1 при x>2 2/3 Выпишите разложение определителя третьего порядка по элементам третьей строки 1 0 -1 2 1 0 1 2 -1 [0 -1] [ 1 -1 ] [ 1 0] 1[1 0] -2[2 0] -1[2 1] Выборочная совокупность задана таблицей распределения... Xi 5 7 10 15 Ni 2 3 8 7 11.96 Составить каноническое уравнение прямой, проходящей через точку М(2;0;-3) параллельно вектору a(2;-3;5) x-2/2=y/-3=z+3/5 По данному ряду распределения случайной величины X найти P(1<X<3) Xi -2 0 2 4 Pi 0.2 0.4 0.3 0.1 0.3 В урне 3 белых и 2 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян белый шар. 0.5
Новый фильм может демонстрироваться в 12 кинотеатрах. Вероятность того, что его показывают в 8 из них, равна 0.8, а для остальных четырех эта вероятность равна 0.5. Вероятность того, что в кинотеатре, выбранном наугад, можно посмотреть этот фильм, равна... 0.7 Вычислите предел функции lim sin6x/sin2x 3 Вычислить площадь фигуры, заключенной между линиями:y=8+2x-x^2; 2x-y+4=0 10.3/2 Составить уравнение прямой, проходящей через точку М(-1;-2) параллельно прямой 7x+2y-3=0 7x+2y+11=0 Найти дисперсию следующих измерений: 1027,1025,1023,1025,1026, 1024 1.67 Вычислите предел функци lim3x ^2—x/x^2+2x -1/2 Вычислить площадь фигуры, ограниченной линиями: y=cosx,x=-п/2,х =п/2,y=0 2 Из генеральной совокупности извлечена выборка объемом n=50, если X=3.44, то несмещенная оценка дисперсии генеральной совокупности приближенно равна...Xi 1 4 5 7 Mi 20 10 14 6 4.74
Из генералной совокупности извлечена выборка объема n=50 Xi 1 2 3 4: Ni 12 n^2 10 9 19 В урне 2 белых и 2 черных шара. Один шар утерян. Вытянутый после этого шар оказался белый. Найти вероятность того, что утерян белый шар. 0,67 Lim(1+1/x)^5x+1 E^5
Определитель [0 1 0] [2 0 0] [0 0 3a-2]=0 2/3
Бесконечность
Дано: P(A) = 0,4; P(B) = 0,1; P(A+B) = 0,48. Найти вероятность совместного появления А и В. 0.02 Расстояние между точками В(-3;-1) и D(9;4) равно 13
Интервальной оценкой параметра закона распределения генеральной совокупности называется
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 848; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |



 Найти длину пройденного пути, пройденного телом от начала движения до его остановки
Найти длину пройденного пути, пройденного телом от начала движения до его остановки


 2. Если события А и В несовместны,
2. Если события А и В несовместны,  3. Если события А и В образуют полную группу, то
3. Если события А и В образуют полную группу, то  4. Если события А и В зависимы, то
4. Если события А и В зависимы, то  5. Если события А и В совместны, то
5. Если события А и В совместны, то  6. Если события А и В несовместны, то
6. Если события А и В несовместны, то  и среднее квадратическое отклонение
и среднее квадратическое отклонение  Считая, что срок службы каждой лампы является нормально распределенной случайной величиной, определить с надежностью 0,9 ширину доверительного интервала для математического ожидания.
Считая, что срок службы каждой лампы является нормально распределенной случайной величиной, определить с надежностью 0,9 ширину доверительного интервала для математического ожидания. . Сделана случайная выборка с возвратом объема
. Сделана случайная выборка с возвратом объема  . Найти с надежностью
. Найти с надежностью  точность выборочной средней.
точность выборочной средней.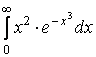

 =
= 
 и
и  , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид: 
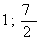
 ширину доверительного интервала для генеральной средней, если
ширину доверительного интервала для генеральной средней, если 


 равен...
равен... Найдите ускорение точки в момент времени
Найдите ускорение точки в момент времени




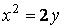 и
и 
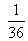
 Неопределенный интеграл от этой функции равен...
Неопределенный интеграл от этой функции равен...
 равно...
равно... и прямой
и прямой 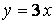 вокруг оси Ох
вокруг оси Ох

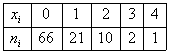
 и осью
и осью 

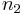
 равен...
равен... и
и 

 равен...
равен...
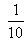




 Найти путь, пройденный телом за первые 3с
Найти путь, пройденный телом за первые 3с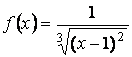

 вычислена выборочная дисперсия
вычислена выборочная дисперсия  . Тогда исправленная дисперсия
. Тогда исправленная дисперсия  для этой выборки равна...
для этой выборки равна... ,
,  ,
,  ,
, 

 . Найти методом моментов параметры а и в равномерного закона.
. Найти методом моментов параметры а и в равномерного закона. , то конкурирующей может быть гипотеза...
, то конкурирующей может быть гипотеза...
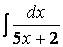

 , заданной функцией распределения
, заданной функцией распределения 
 и прямой
и прямой 

 и прямой
и прямой  , а
, а  . Оценить с доверительной вероятностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности по выборочному среднему с помощью доверительного интервала
. Оценить с доверительной вероятностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности по выборочному среднему с помощью доверительного интервала
 и
и  вокруг оси Оу
вокруг оси Оу
 по данному распределению выборки:
по данному распределению выборки: . Найти вероятность того, что при 150 испытаниях частость появления этого события будет отличаться от его вероятности не более чем на 0,03.
. Найти вероятность того, что при 150 испытаниях частость появления этого события будет отличаться от его вероятности не более чем на 0,03.

 .
.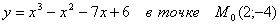




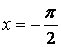

 и прямой
и прямой 

 нормально распределенной величины Х, если по выборке объёма n=49 вычислена выборочная средняя
нормально распределенной величины Х, если по выборке объёма n=49 вычислена выборочная средняя  =10..Генеральное среднее квадратическое отклонение
=10..Генеральное среднее квадратическое отклонение  =14. Табличные значения функции Лапласа: Ф(0,95)=0,329; Ф(1,96)=0,475
=14. Табличные значения функции Лапласа: Ф(0,95)=0,329; Ф(1,96)=0,475 ,
,  ,
, 
 и
и 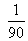
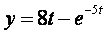 Тогда ее дифференциал равен...
Тогда ее дифференциал равен...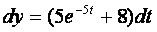



 закона распределения генеральной совокупности называется
закона распределения генеральной совокупности называется

 =np
=np 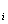 ,где n-объём выборки
,где n-объём выборки 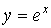 ,
, 

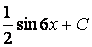

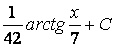



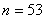 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:  Тогда число вариант
Тогда число вариант  в выборке равно....
в выборке равно....



