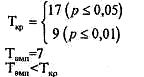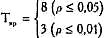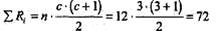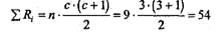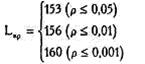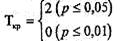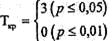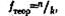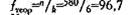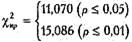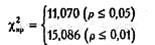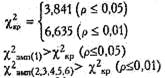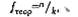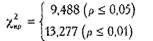Использование критерия Т Вилкоксона для решения задачи 5

Сформулируем гипотезы.

H₀: Интенсивность положительных сдвигов не превосходит интенсивно­сти отрицательных сдвигов.

H₁: Интенсивность положительных сдвигов превосходит интенсивность отрицательных сдвигов.

В Табл. 20 нами уже просуммированы ранги "редких", в данном случае, отрицательных, сдвигов. Сопоставляем эти значения с максимальными значениями Т, при которых различия еще могут считаться достоверными.

Для шкалы "Активное слушание", n =12:

Ответ: H₀ отклоняется. Преобладание положительных сдвигов по навыкам активного слушания неслучайно (р <0,05). Для шкалы "Снижение напряжения", n= 12:

Ответ: H₀ отклоняется. Принимается H₁. Преобладание поло­жительных сдвигов по навыку снижения напряжения не является слу­чайным (р <0,01).

Для шкалы "Аргументация", n =9:

т_эмп=0

т_эмп <т_кр

Ответ: H₀ отвергается. Принимается H₁. Преобладание поло­жительных сдвигов по навыкам аргументации неслучайно (р <0,01).

Итак, участники ощущают значимые положительные сдвиги по всем трем группам коммуникативных навыков.

В данном случае критерий Т доказал свою большую мощность по сравнению с критерием знаков. Он подтвердил ранее установленные различия на высоком уровне значимости (р <0,01) и позволил выявить их для шкалы "Активное слушание" (р <0,05).

Однако мы не можем интерпретировать полученные результаты в терминах эффективности тренинга по меньшей мере по двум причинам:

1) у нас не было контрольной группы, у которой измерялись бы те же показатели с тем же интервалом времени;

2) показатели самооценки после тренинга могли отражать желание испытуемых косвенно поблагодарить тренера за его работу.

Несмотря на это, все-таки есть смысл ответить на второй вопрос задачи, проверив, различаются ли между собой величины сдвигов по трем разным шкалам. Со всеми возможными поправками на индивидуальные тенденции к завышению или занижению самооценок, различия в сдвигах все же отражают относительную эффективность тренинговых воздействий по трем направлениям.

Вопрос 2: Произошли ли по трем видам навыков разные сдвиги или эти сдвиги для разных навыков примерно одинаковы?

Величины сдвигов получены по трем разным шкалам для одной и той же выборки испытуемых. Для того, чтобы определить, различаются ли величины сдвигов, полученных по трем шкалам, применимы критрий χ ²_r Фридмана и L Пейджа.

Таблица 21

Сдвиги в оценках уровня развития коммуникативных навыков и их ранги (n =12)

Код имени	Признак 1: Активное слушание	Признак 2: Снижение эмоционального напряжения	Признак 3: Аргументация
Оценка	Ранг	Оценка	Ранг	Оценка	Ранг
	Ис.		1,5		1,5
	Я.
	Ин.
	Р.
	К.	–2^4			2.5	1,5	2,5
	Н.		1,5		1,5
	Ен.				1,5		1,5
	Ле.	–1			2,5		2,5
	Ли.		2,5		2,5
	Т.				1,5		1,5
	Ет.	–1		–2
	Б		1,5				1,5
Суммы		25 (21)		24,5 (18,5)		22,5 (14,5)
Средние	1,25	1,58	1,25

_____________

⁴ Отрицательную величину считаем меньшей величиной и приписываем ей, соот­ветственно, меньший ранг. Может получиться так, что большую величину ранга -третий ранг - получит значение 0, как это имеет место у испытуемого Ет. (№11). В каком-то смысле при двух отрицательных сдвигах третий нулевой сдвиг является положительным, но это можно и оспаривать. Поэтому целесообразно рассчитать значение L отдельно для всех испытуемых и для тех испытуемых, у кого нет отри­цательных сдвигов (п=9). Соответствующие суммы приведены в скобках.

Проранжируем сдвиги по трем шкалам для каждого испытуемого (Табл. 21). Ранжирование, как мы помним, производится по строкам.

Поскольку количество замеров с =3, т. е. меньше 6, а количество испытуемых гг=12, мы можем остановить выбор на критерии тенденций L Пейджа. Такая возможность благоприятна, так как критерий L по мощ­ности превосходит критерий χ ²_r (см., например, задачу 3 и ее решение).

Проверим соответствие сумм рангов расчетным суммам. Сумма рангов по всей выборке составляет 25+24,5+22,5=72. Расчетная сумма:

Сумма рангов по усеченной выборке (n =9) составляет 21+18,5+14,5=54. Расчетная сумма:

В обоих случаях суммы рангов совпадают с расчетными, мы мо­жем перейти к дальнейшим действиям.

Сформулируем гипотезы, ориентируясь на значения ранговых сумм;

H₀: Тенденция к меньшему сдвигу по шкале "Аргументация", проме­жуточному сдвигу по шкале "Снижение напряжения" и большему сдвигу по шкале "Активное слушание" является случайной.

H₁: Тенденция к меньшему сдвигу по шкале "Аргументация", промежу­точному сдвигу по шкале "Снижение напряжения" и большему сдвигу по шкале "Активное слушание" не является случайной.

Определим эмпирические значения критерия L по всей выборке в целом:

L_эмп =∑(T_j·j)=(22,5·1)+(24_,5·2)+(25·3)=22,5+49+75=146_,5

По Табл. VIII Приложения 1 определяем критические значения L для п= 12, с =3:

L_эмп =146,5

L_эмп < L_кр

H₀ принимается.

Определим эмпирическое значение критерия L для усеченной выборки:

L_эмп =(14,5 · 1)+(18,5 · 2)+(21 · З)=14,5+37+63=114,5

Определяем по Табл.VIII Приложения 1 критические значения L при n =9:

L_эмп =114,5

L_эмп < L_кр

H₀ принимается.

Ответ: H₀ принимается и для полной, и для усеченной выборки. Тенденция к меньшему сдвигу по шкале "Аргументация", промежуточ­ному сдвигу по шкале "Снижение напряжения" и наибольшему сдвигу по шкале "Активное слушание" является случайной.

Итак, общий вывод таков: сдвиги в показателях по трем видам коммуникативных навыков достоверны, но указать, в каком из видов навыков участники ощущают больший сдвиг, а в каком - меньший, на основании этих данных невозможно.

Вопрос 3: Уменьшается ли расхождение между "идеальным" и реальным уровнями владения навыками после тренинга?

Сокращение расхождения между индивидуальным идеалом и са­мооценкой - один из главных показателей эффективности психотерапев­тического воздействия (Rogers С.,1961,р.236; Роджерс К.,1995,с.292). Сближение самооценки реального Я и идеального Я происходит в большинстве случаев аа счет повышения реальной самооценки, но мо­жет снизиться и уровень идеальных требований к себе благодаря пере­ключению на более реалистичные и менее "наказующие" цели.

Итак, мы проверяем, оказал ли тренинг психотерапевтическое воздействие на участников. Как правило, испытуемые не предполагают, что у них измеряется не абсолютный уровень самооценки или "идеала" и, даже, не расхождение между ними, а расхождение между расхожде­ниями, сдвиг в величине этого расхождения после тренинга. Можно предположить, что этот показатель более объективно отражает проис­ходящие изменения. По крайней мере, он в меньшей степени подверг­нут влиянию фактора социальной желательности.

Поскольку мы сопоставляем 2 разных представляемых или умо­зрительных условия измерения на одной и той же выборке испытуемых и по одному и тому же набору показателей, применимы критерии зна­ков и Т Вилкоксона.

Поскольку расхождения варьируют в достаточно широком диапа­зоне - от 3 до 5, целесообразнее использовать критерий Т Вилкоксона.

В Табл. 21 по каждой шкале представлены 4 показателя: рас­хождение между идеальным и реальным уровнями до тренинга, после тренинга, разность между расхождениями "после" и "до" и ранги этих разностей (сдвигов).

Таблица 21

Сдвиг в величинах расхождения между "идеалом" и реальным уровнем развития коммуникативных навыков

Код имени частника	Активное слушание	Снижение напряжения	Аргументация
До	после	Сдвиг (после -до)	Ранг сдвига	до	после	Сдвиг Ранг (после сдвига — до)	до	после	Сдвиг (после -до)	Ранг сдвига
	Ис.				—			–	3.5			-1	3,5
	Я.				—				-				3,5
	Ин.				—			-1	3,5			-1	3,5
	Р.			-1					3,5				–
	К.				4,5				-				3,5
	Н.			-1				-1	3,5			-1	3,5
	Ен.			-4				-3				-2
	Ле.				-				-				–
	Ли.			-1				-1	3.5				—
	Т.				-				-				3,5
	Ет.				4,5				3,5				—
	Б.				_			-5					–
Всего сдвигов
Типичный сдвиг	Отрицательный	Отрицательный	Отрицательный
Сумма ран­гов нетипич­ных сдвигов								10,5				10.5

В Табл. 21 выделены величины нетипичных, более редко встречающихся, сдвигов, и ранги их абсолютных значений. Мы видим, что большинство сдвигов - это нулевые или отрицательные сдвиги. Это означает, что расхождение между идеалом и самооценкой чаще умень­шается или остается на прежнем уровне, чем увеличивается. Однако нас сейчас интересует именно уменьшение расхождения между идеаль­ным и реальным Я, а поэтому все нулевые сдвиги придется исключить из рассмотрения.

Сформулируем гипотезы.

H₀: Сближение идеального и реального уровней навыков после тре­нинга не является преобладающей тенденцией.

H₁: Сближение идеального и реального уровней навыков после тренинга является преобладающей тенденцией.

Сближение выражается в отрицательном, типичном, сдвиге рас­хождения между идеальным и реальным уровнями.

Определяем критические значения критерия Т и сопоставляем их с эмпирическими значениями. По шкале "Активное слушание"", n =6:

T_эмп = 9

T_эмп > T_кр

Нд принимается.

По шкале "Снижение напряжения", n =8:

T_эмп = 10,5

T_эмп > T_кр

Но принимается.

По шкале "Аргументация", п=7:

T_эмп = 10,5

T_эмп > T_кр

Но принимается.

Ответ: Т - критерий Вилкоксона не позволяет отвергнуть нуле­вую гипотезу. Уменьшение расхождения между идеальным и реальным уровнями навыков не является доминирующей тенденцией.

Исследователь может утешать себя тем, что в процессе тренинга участники ощутили новые горизонты развития... Действительно, про­изошли достоверные положительные сдвиги не только в оценке реаль­ного уровня владения коммуникативными навыками (см. выше), но и достоверные положительные сдвиги в оценке идеального уровня. Кроме того, в исследованиях К. Роджерса речь идет не о самооценке уровня владения коммуникативными навыками, а о более глубоких аспектах личностной самооценки в методе Q - сортировки. Учитывая малый объ­ем выборки, полученный результат можно считать лишь предваритель­ным.

Решение задачи 6

Вопрос 1: Можно ли утверждать, что разные картины методики Хекхаузена обладают разной побудительной силой в отношении моти­вов: а) "надежда на успех"; б) "боязнь неудачи"?

Для того, чтобы ответить на этот вопрос, необходимо сопоставить распределение реакций "надежда на успех" и реакций "боязнь неудачи" с равномерным распределением. Тем самым мы проверим, равномерно ли распределяются реакции "надежды на успех" по шести картинам и равно­мерно ли распределяются реакции "боязни неудачи" по шести картинам.

Количество наблюдений достаточно велико, чтобы мы могли ис­пользовать любой из классических критериев - χ ² или λ. Однако, как мы помним, картины в данном исследовании предъявлялись разным испытуемым в разных последовательностях, следовательно, мы не мо­жем говорить об однонаправленном изменении признака в какую-либо одну сторону: все разряды (картины) следуют друг за другом в слу­чайном порядке. Это является веским основанием для применения кри­терия χ ² и отказа от критерия λ.

Рассмотрим оба аспекта поставленного вопроса последовательно.

А) Равномерно ли распределяются реакции "надежды на успех" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "надежды на успех" не отличается от рав­номерного распределения.

H₁: Распределение реакций "надежды на успех" отличается от равно­мерного распределения.

Рассчитаем теоретические частоты для равномерного распределе­ния по формуле:

где n - количество наблюдений,

k - количество разрядов.

В данном случае количество наблюдений - это количество реак­ций "надежды на успех" у 113 испытуемых. Таких реакций зарегистри­ровано 580, следовательно, n =580. Количество разрядов - это количе­ство стимульных картин, следовательно, k=6. Определяем f _теор:

Количество степеней свободы V определяем по формуле:

v = k -l=6-l=5

Итак, поправка на непрерывность не нужна, мы можем произво­дить все расчеты по общему алгоритму. Они представлены в Табл.22.

Таблица 22

Расчет критерия χ ² при сопоставлении распределения реакций "надежды на успех" по 6 картинам с равномерным распределением

Разряды-картины методики	Эмпирические частоты реакций "надежды на успех" fэ	Теоретические частоты реакции "надежды на успех" fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"		96,67   96,67   96,67   96,67   96,67   96,67	9,33   5,33 11,33   -46,67   2,33   18,33	87,05   28,41   128,37   2178,09   5,43   335,99	0,90   0,29   1,33   22,53   0,06   3,48
Суммы					28,59

Определяем критические значения χ ² для v =5:

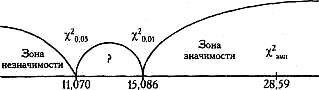
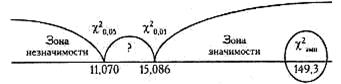
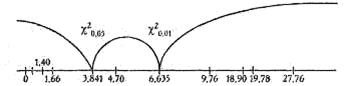
Построим "ось значимости".

χ²_эмп = 28,59

χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение реак­ций "надежды на успех" по шести картинам методики Хекхаузена от­личается от равномерного распределения (р <0,01).

Б) Равномерно ли распределяются реакции "боязни неудачи" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "боязни неудачи" не отличается от равно­мерного распределения.

H₁: Распределение реакций "боязни неудачи" отличается от равномер­ного распределения.

В данном случае количество наблюдений - это число реакций "боязни неудачи", следовательно, n =516; количество разрядов - это число стимульных картин, как и в предыдущем случае, следовательно, k=6. Определяем f _теор

f _теор =⁵¹⁶/₆=86

Количество степеней свободы v = k —1=6—1=5. Поправка на не­прерывность здесь тоже, естественно, не нужна.

Все дальнейшие расчеты проделаем по алгоритму в таблице.

Таблица 23

Расчет критерия при сопоставлении распределения реакций "боязни неудачи" по 6 картинам с равномерным распределением

Разряды-картины методики	Эмпирические частоты реакций "боязни неудачи" fэ	Теоретические частоты реакции "боязни неудачи" fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"			-52     -29   -66		31,44   102.74   31,44   0.01   9.78   50,65
Суммы					226,06

 

Критические значения χ²при v =5:

χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение прояв­лений "боязни неудачи" по шести стимульным картинам отличается от равномерного распределения (р <0,01).

Итак, реакции "надежды на успех" и реакции "боязни неудачи" неравномерно проявляются в ответ на 6 стимульных картин. Однако это еще не означает, что эти картины являются неуравновешенными по направленности воздействия. Может оказаться так, по крайней мере теоретически, что одни и те же картины вызывают большинство реакций обоих типов, а другие картины почти не вызывают реакций или вызывают их достоверно меньше. В этом случае оба эмпирических распределения отличались бы от равномерного, но не различались бы между собой.

Проверим, различаются ли картины теперь уже не по количеству вы­зываемых реакций, а по их качеству, то есть вызывают ли одни картины скорее реакции "надежды на успех", а другие - реакции "боязни неудачи"

Вопрос 2: Можно ли считать стимульный набор методики Хекхаузена неуравновешенным по направленности воздействия?

Решим эту задачу двумя способами: а) путем сравнения распре­деления реакций "надежда на успех" с распределением реакций "боязнь неудачи" по 6-и картинам; б) путем сопоставления распределения реак­ций на каждую картину с равномерным распределением.

Выясним, совпадают ли распределения реакций по двум карти­нам. Для этого сформулируем гипотезы.

H₀: Распределения реакций "надежда на успех" и реакций "боязнь не­удачи" не различаются между собой.

H₁: Распределения реакций "надежда на успех" и "боязнь неудачи" различаются между собой.

Для того, чтобы облегчить себе задачу подсчета теоретических частот, воспроизведем таблицу эмпирических частот и дополним ее.

Таблица 24

Эмпирические и теоретические частоты распределения реакций "надежда на успех" и "боязни неудачи"

Разряды - картины	Эмпирические частоты	Суммы	Теоретические частоты	Суммы
Реакций "надежда на успех"	Реакций "боязнь неуда­чи"		Реакций "надежда на успех"	Реакций "боязнь неуда­чи"
	"Мастер измеря­ет деталь" "Преподаватель и ученик" "В цехе у маши-   "У двери дирек­тора"   "Человек в бюро"   "Улыбающийся юноша"		А   В   д   ж   и   л		Б   Г   Е     К   M		129,1   149,2   75,1   72,5   82,6   71,4	А   В   Д   Ж   И   Л	114,9   132,8   66,9   64,5   73,4   63,6	Б   Г   Е     К   М
Суммы

Расчет теоретических частот осуществляется по известной нам формуле:

Произведем расчеты.

f_{А теор}=244·580/1096=129,1

f_{Б теор}=244·516/1096=114,9

f_{В теор}=282·580/1096=149,2

f_{Г теор}=282·516/1096=132,8

f_{Д теор}=142·580/1096=75,1

f_{Е теор}=142·516/1096=66,9

f_{Ж теор}=137·580/1096=72,5

f_{З теор}=137·516/1096=64,5

f_{И теор}=156·580/1096=82,6

f_{К теор}=156·516/1096=73,4

f_{Л теор}=135·580/1096=71,4

f_{М теор}=135·516/1096=63,6

 

По Табл. 24 мы видим, что сумма всех теоретических частот равна общему количеству наблюдений, а попарные суммы теоретических частот по строкам равны суммам наблюдений по строкам.

Расчеты критерия χ²будем производить по известному алгоритму. Поправка на непрерывность не вносится, так как v >1:

v =(r -l)(c -l)=(6-l)(2-l)=5

Результаты всех операций по Алгоритму 13 представлены в Табл. 25.

Таблица 25

Расчет критерия χ²при сопоставлении эмпирических распределений реакций "надежды на успех" (НУ) и "боязни неудачи" (БН)

Ячейки таблицы частот	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
	А		129,1	-23,1	533,61	4,13
	Б		114,9	23,1	533,61	4,64
	В		149,2	-47,2	2227,84	14,93
	Г		132,8	47,2	2227,84	16,78
	Д		75,1	32,9	1082,41	14,41
	Е		66,9	-32,9	1082,41	16,18
	Ж		72,5	-22,5	506,25	6,98
			64,5	22,5	506,25	7,85
	И		82,6	16,4	268,96	3,26
	К		73,4	-16,4	268,96	3,66
	Л		71,4	43,6	1900,96	26,62
	М		63,6	-43,6	1900,96	29,89
Суммы,					149,33

 

Критические значения χ²при v =5 нам уже известны:

Построим "ось значимости".

χ²_эмп > χ²_кр

Ответ: H₀ отвергается. Принимается H₁. Распределения реакций "надежды на успех" и "боязни неудачи" различаются между собой.

Теперь выясним, совпадают ли распределения реакций по каждой картине. Сформулируем гипотезы.

H₀: Реакции двух видов в ответ на картину №1 (№2, №3... №6) распределяются равномерно.

H₁: Реакции двух видов в ответ на картину №1 (№2, №3... №6) распределяются неравномерно.

Реакции "надежды на успех" будем обозначать как НУ, реакции "боязни неудачи" - как БН.

Подсчитаем теоретические частоты для каждой из шести картин, по формуле:

где n общее количество реакций обоих направлений на данную картину; k - количество разрядов, в данном случае количество видов реакции (k =2).

f_{1 теор} =244/2=121;

f_{2 теор} =282/2=141;

f_{3 теор} =142/2=71;

f_{4 теор} =137/2=68,5

f_{5 теор} =156/2=78

f_{6 теор} =135/2=67,5

В данном случае число степеней свободы v =l:

v = k —1=2—1=1.

Следовательно, мы должны сделать во всех шести случаях по­правку на непрерывность. Проведем расчеты отдельно для каждой кар­тины (см. Табл. 26).

Таблица 26

Расчет критерия χ²при сопоставлении распределений реакций на каж­дую из шести картин с равномерным распределением

 

Определим критические значения для v =l:

 

Ответ: H₀ отклоняется для всех картин. H₁принимается для картин 2, 3, 4, 5 и 6: реакции двух видов в ответ на эти картины рас­пределяются неравномерно.

Если представить данные графически (Рис. 26), то легко можно видеть, что картины №6, №3 и №5 вызывают достоверно больше реакций "надежды на успех", а картины №2, №1 и №4 - достоверно больше реакций "боязни неудачи".

Стимульный набор методики Х. Хекхаузена оказался неуравнове­шенным по направленности стимулирующего воздействия.

Рис. 26. Соотношения частот реакций "надежда на успех" (незаштрнхованные столбн-ки) н реакций "боязнь неудачи" (заштрихованные столбики) по разным картинам мето­дики Х.Хекхаузена

 

Вместе с тем, из Рис. 26 мы можем заметить, что если частоты реакций "боязни неудачи" достаточно монотонно возрастают при пере­ходе от картины №6 к картине №3, а затем к №5, №4, №1 и №2, то частоты реакций "надежда на успех" по всем картинам, за исключе­нием картины №4, оказываются примерно на одном уровне, в диапазо­не от 99 до 115. Каждый исследователь сам для себя решает вопрос о том, что для него важнее - абсолютные показатели стимулирующего воздействия или их соотношения. Данный метод поможет ему решить зада­чи и первого, и второго типа.

Решение задачи 7

Вопрос 1: Можно ли утверждать, что распределение запретов не является равномерным?

Поскольку количество разрядов (запретов) k>3, иперечень из пяти запретов представляет собой номинативную шкалу, мы можем ис­пользовать только критерий χ².

Если бы участники тренинга называли разные запреты с одина­ковой частотой, то каждый из пяти запретов встречался бы равноверо­ятно с остальными.

Сформулируем гипотезы.

H₀: Распределение частот встречаемости пяти запретов не отличаетсяот равномерного распределения.

H₁: Распределение частот встречаемости пяти запретов отличается от равномерного распределения.

Определим f _теор по формуле:

где n - общее количество наблюдений, в данном случае назван­ных запретов (n =281); k - количество категорий запретов (k =5).

f _теор =281/5=56,2

Определим число степеней свободы v:

v = k -l=5-l=4.

Поправки на непрерывность делать не требуется. Все расчеты представим в таблице.

Таблица 27

Расчет критерия χ²при сопоставлении эмпирического распределения частот встречаемости 5-и психологических запретов с равномерным распределением

Разряды - вид запрета	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)^2	(fэ- fт)^2/ fт
1, Не давай психологических поглаживаний 2. Не принимай... 3. Не проси... 4. Не отказывайся... 5. Не давай себе...		56,2     56,2 56,2 56,2 56,2	-12,2     -11,2 +41,8 +1,8 -20,2	148,8     125,4 1747,2 3,2 408,0	2,65     2,23 31,09 0,06 7,26
Суммы					43,29

 

Определим критические значения χ²для v =4:

Построим "ось значимости"

Ответ: χ²_эмп > χ²_кр (р ≤0,01)

H₀ отклоняется. Принимается H₁. Распределение частот встре­чаемости пяти психологических запретов отличается от равномерного распределения (р <0,01).

 

Вопрос 2: Можно ли утверждать, что запрет "Не проси" встре­чается достоверно чаще остальных?

Для того, чтобы ответить на этот вопрос, мы можем попробовать сопоставить запрет "Не проси" последовательно со всеми остальными запретами, объединяя их попарно.

H₀: Распределение выборов между запретами "Не проси" и "Не да­вай" не отличается от равномерного распределения.

H₁: Распределение выборов между запретами "Не проси" и "Не давай" отличается от равномерного распределения.

Аналогичные гипотезы могут быть сформулированы для всех остальных пар запретов.

При сопоставлении двух запретов число разрядов k=2, следовательно, количество степеней свободы v = k —1=1. Это означает, что нам необходимо делать поправку на непрерывность.

Рассчитаем теоретические частоты для каждой из сопоставляемых пар запретов.

где п - сумма частот, приходящихся на данную пару запретов; k - количество сопоставляемых категорий запретов (k= 2 ).

Определим теоретические частоты для всех возможных пар запретов.

f _{теор 1-2}=(44+45)/2=44,5

f _{теор 1-3}=(44+98)/2=71

f _{теор 1-4}=(44+58)/2=51

f _{теор 1-5}=(44+36)/2=40

f _{теор 2-3}=(45+98)/2=71,5

f _{теор 2-4}=(45+58)/2=51,5

f _{теор 2-5}=(45+36)/2=40,5

f _{теор 3-4}=(98+58)/2=78

f _{теор 3-5}=(98+36)/2=67

f _{теор 4-5}=(58+36)/2=47

Теперь подсчитаем значения критерия χ² (Табл. 28).

 

Таблица 28.

Расчет значений критерия при попарном сопоставлении частот запретов

Сопоставляемые виды запретов	Эмпирические частоты fэ	Теоретические частоты fт	(fэ – fт)	(|fэ – fт| -O,5)	(|fэ – fт| -O,5)^2	(|fэ – fт| -O,5)^2 ^__________ fт
	«Не давай» «Не принимай Суммы		44,5 44,5   99,0	-0,5 + 0,5
	«Не давай» «Не проси» Суммы		71,0 71,0 142,0	-27,0 + 27,0	26,5 26,5	702,25 702,25	9,89 9,89 19,78
	«Не давай» «Не отказывайся» Суммы		51,0 51,0   102,0	-7,0 + 7,0	6,5 6,5	42,25 42,25	0,83 0,83   1.66
	«Не давай» «Не давай себе» Суммы		40,0 40,0   80,0	+ 4,0 -4,0	3,5 3,5	12,25 12,25	0,31 0,31   0,62
	«Не принимай» «Не проси» Суммы		71,5   71,5 143,0	-26,5   +26,5	26,0   26,0	676,00   676,00	9,45   9,45 18,90
	«Не принимай» «Не отказывайся» Суммы		51,5   51,5   103,0	-6,5   + 6,5	6,0   6,0	36,00   36,00	0,70   0,70   1,40
	«Не принимай» «Не давай себе» Суммы		40,5   40,5   81,0	+ 4,5   -4,5	4,0   4,0	16,00   16,00	0,40   0,40   0,80
	«Не проси» «Не отказывайся» Суммы		78,0 78,0   156,0	+ 20,0 -20,0	19,5 19,5	380,25 380,25	4,88 4,88   9,76
	«Не проси» «Не давай себе* Суммы		67,0 67,0   134,0	+ 31,0 -31,0	30,5 30,5	930,25 930,25	13,88 13,88   27,76
	«Не отказывайся» «Не давай себе» Суммы		47,0   47,0   94,0	+ 11,0   -11,0	10,5   10,5	110,25   110,25	2,35   2,35   4,70

Определим критические значения χ²для v =l:

Построим "ось значимости".

Мы видим, что в некоторых случаях χ²_эмп > χ²_кр, а в некоторых - χ²_эмп < χ²_кр.

Мы можем суммировать полученные данные, построив матрицу, в которой какими-либо знаками будет отмечено, являются ли различия между данной парой запретов достоверными или недостоверными. На­пример, это могут быть указания на уровень значимости различий.

Запреты	1 запрет 2 запрет 3 запрет 4 запрет 5 запрет
1 запрет	—	—	p <0,01	—