
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие сведения из теории погрешностей.Содержание книги Поиск на нашем сайте
Введение. Основной целью проведения лабораторного практикума по физике является расширение и закрепление теоретических знаний, получаемых на лекциях, а также проверка научно-теоретических положений экспериментальным путем. Для достижения этой цели студенту необходимо: - заблаговременно готовиться к выполнению лабораторных работ с тем, чтобы иметь достаточно ясное представление по теории вопросов, относящихся к теме каждой лабораторной работы, а также методике выполнения этой работы; - выполнять заданное количество лабораторных работ (по графику, составленному преподавателем) в соответствии с требованиями, изложенными в методических указаниях к ним; соответствующим образом обработать полученные результаты и оформить отчет по этой работе; - защитить выполненные работы на текущих или итоговых занятиях. Для получения разрешения выполнять данную лабораторную работу каждый студент должен: 1. Представить конспект по лабораторной работе (ответы на контрольные вопросы в обязательном порядке). 2. Иметь бланк отчета по этой работе, а также подготовленный заранее черновик. 3. Доказать в беседе с преподавателем свою готовность самостоятельно и осмысленно выполнять работу.
Правила вычисления абсолютной погрешности.
Таблица погрешностей косвенных измерений для наиболее употребляемых функций.
Запись результата измерений имеет вид: При этом необходимо соблюдать следующие правила: - погрешность DC округляется до двух значащих цифр, если первая из них 1 или 2, а во всех остальных случаях до одной значащей цифры, - число знаков после запятой в погрешности и в результате должно совпадать (позицию округления результата определяет величина абсолютной погрешности), -порядок величины, как правило, выносится за скобки. Например, u=(1,23±0,17)×103 м/с. Международная система единиц – СИ
Множители и приставки СИ для образования десятичных, кратных и дольных единиц
Лабораторная работа № 1 НЕУПРУГИЙ УДАР Цель работы: ознакомиться с практическим применением закона сохранения импульса на примере определения скорости одного из тел при неупругом ударе.
Приборы и принадлежности: баллистический маятник, шарик. Схема экспериментальной установки:
Методика исследования и описание установки При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим. Примером указанного взаимодействия является соударение шарика массой m и начальной скоростью На основании закона сохранения импульса имеем:
где В результате столкновения маятник придет в движение и отклонится на угол j, при этом кинетическая энергия переходит в потенциальную энергию и на основании закона сохранения энергии можно записать следующее уравнение:
где h – максимальная высота поднятия центра тяжести маятника. Отсюда
Из подобия треугольников ABC и OBO’ (рис.1) следует
Но
Решая совместно выражения (1),(3),(4), получим уравнение для определения начальной скорости шарика:
Для определения скорости тела - шарика, вызывающего смещение маятника из первоначального состояния покоя, используется установка, схема которой приведена на рисунке. Установка состоит из массивного цилиндра 1, подвешенного на практически нерастяжимом стержне 2. Внутри цилиндра 1 имеется углубление, заполненное пластилином. На некотором расстоянии от него по оси расположена трубка 3, внутри которой размещена пружина. В трубке сверху имеется отверстие 4, предназначенное для опускания внутрь нее шарика 5. При этом пружина должна быть в сжатом состоянии. После нажатия на спусковое устройство 6 пружина выбрасывает шарик из трубки с некоторой скоростью
Порядок выполнения работы 1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей мыши на экране кнопку «Теория и методика проведения работы». 3. Откройте flash - анимацию, для этого щелкните кнопку «Эксперимент». 4. По указанию преподавателя задайте данные для коэффициента жесткости k, x, m, l, M и щелкните ОК. 5. С помощью мыши оттяните пружину пистолета и отпустите ее. 6. Запишите значения М, m, l, j в таблицу. 7. Повторите опыт 10 раз, каждый раз записывая полученные значения в таблицу. 8. Произведите вычисления предлагаемых величин. 9. Сделайте вывод о проделанной работе. 10. Ответьте на контрольные вопросы.
Обработка результатов измерений 1. Смещение центра тяжести маятника определить по формуле
2. Начальная скорость шарика определяется по формуле (5). 3. Расчет относительной погрешности провести по формуле
4. Расчет абсолютной погрешности провести по формуле
где Δ M, Δ m, Δ l, Δj, Δg – абсолютные погрешности измерения соответственно массы маятника и шарика, расстояния от точки подвеса до центра тяжести маятника, угла отклонения маятника и ускорения свободного падения.
Таблица измерений:
Контрольные вопросы: 1. Что понимают под ударом? Дайте определение абсолютно упруго и неупругого удара. 2. Дайте определение импульса тела. 3. Сформулируйте закон сохранения импульса. 4. Запишите закон сохранения импульса для данной установки. 5. Можно ли считать, что кинетическая энергия шарика, в случае неупругого удара полностью переходит в потенциальную энергию маятника? 6. Запишите формулу для определения изменения кинетической энергии системы двух сталкивающихся тел при абсолютно неупругом, прямом центральном ударе.
Лабораторная работа №2. Теоретическое введение Основным законом динамики является второй закон Ньютона, связывающий понятия кинематики (скорость, ускорение) с динамическими понятиями (масса, сила, импульс тела). Второй закон Ньютона (для тел постоянной массы) можно сформулировать так: сила, действующая на тело (равнодействующая всех сил), равна произведению массы тела на его ускорение: Закон в этом виде можно проверить, если, оставляя постоянной силу, менять массу, тогда или, оставляя постоянной массу, менять силу, тогда
Целью настоящей работы является проверка соотношения (2) при помощи машины Атвуда. Машина Атвуда состоит из вертикальной рейки со шкалой 2. Сверху к рейке прикреплен легкий блок 1, способный вращаться с незначительным трением. Через блок перекинута тонкая капроновая нить 3 с прикрепленными грузами 4 одинаковых масс m. Грузы могут быть установлены на передвигающихся вдоль рейки платформах 5, одна из которых снабжена электромагнитом 6 для удержания грузов. Система двух таких одинаковых по массе покоящихся грузов находится в равновесии. Такая система, выведенная из равновесия легким, толчком руки, движется замедленно, так как постоянно действует сила трения оси блока. При проверке основного закона динамики на описанной установке силой трения пренебрегать нельзя, поскольку ее величина сравнима с силами, приводящими грузы в ускоренное движение. Сила трения в установке компенсируется добавочным грузом массой m1, который помещается на движущий груз, вместе с перегрузками такой же массы Изменение движущей силы осуществляется путем перекладывания добавочных грузов с одного груза на другой. Пример. Если на левом (движущем) грузе лежит восемь дополнительных перегрузков массой m1, а на правом два таких же, то движущей силой будет сила
Если два из добавочных перегрузков перенести с левого груза на правый, то движущей силой будет Сила F2 сообщит системе ускорение
Отношение движущих сил а поделив (3) на (4) получается, что Соотношение сил мы можем найти напрямую (как в выражении 5), а соотношение ускорений определим из кинематических законов: При равноускоренном движении из состояния покоя
Если принять Т.е. отношение ускорений можно заменить обратным отношением квадратов времен. Т.о. измеряя время движения грузов с одной и той же высоты при разных соотношениях перегрузков, можно проверить соотношение (2), заменив его соотношением Порядок выполнения работы 1) Задайте с помощью мыши расстояние от левого груза до левой платформы по своему усмотрению, но не менее 0,4 м (запишите его в таблицу 2.1) и больше его не изменяйте. 2) Из стопки перегрузков справа наложите определённое их количество на левый и правый грузы в соответствии с вашим вариантом (соотношение перегрузков, а значит и движущую силу F1 запишите в таблицу 2.1 (не учитывайте один из тех, что слева т.к. он для компенсации силы трения)). 3) Нажмите кнопку старт и измерьте время движения t1 левого груза до платформы. Запишите его в таблицу 2.1. 4) Повторите пункт 3 ещё 9 раз. Таблица 2.1
5) Переложите один или несколько перегрузков с левого груза на правый или наоборот (соотношение перегрузков, а значит и движущую силу F2 запишите в таблицу 2.1 (не учитывайте один из тех, что слева т.к. он для компенсации силы трения)). 6) Повторите 10 раз пункт 3 для измерения времени t2. Лабораторная работа № 3
Таблица измерений
Контрольные вопросы:
1) Что называется моментом инерции материальной точки и абсолютно твердого тела? 2) Что называется моментом силы относительно неподвижной точки и неподвижной оси, как он направлен, как определяется его модуль? 3) Записать основной закон динамики вращательного движения. 4) Как меняется отношение линейных ускорений груза m, если грузы m1 сдвинуть к центру? 5) Что изменится, если изменить диаметр шкива, на который наматывается нить?
Лабораторная работа №4
Таблица измерений № 1
Таблица измерений № 2
Контрольные вопросы: 1) Что называется силой тяжести? 2) Какое движение называется свободным падением? 3) Почему ускорение свободного падения не одинаково в различных точках земной поверхности? 4) Дайте определение инерциальной и неинерциальной систем отсчета. 5) Какие силы действуют на земные тела, если систему отсчета связанную с Землей считать инерциальной и неинерциальной? Лабораторная работа №5
Определение коэффициента вязкости жидкости
Цель работы: определить коэффициент вязкости жидкости. Приборы и принадлежности: сосуд с жидкостью, секундомер, масштабная линейка, штангенциркуль, шарики. Схема экспериментальной установки:
Методика исследования и описание установки При движении жидкости между ее слоями возникают силы внутреннего трения противостоящие «сдвигу» слоев, действующие таким образом, чтобы уровнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному слою некоторый импульс, что приводит к торможению последнего. Сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения ∆S и градиенту скорости
Величина η называется коэффициентом внутреннего трения или вязкости. Коэффициент вязкости зависит от природы жидкости и для данной жидкости с повышением температуры вязкость уменьшается. При падении шарика в вязкой жидкости на него действуют три силы: 1. Сила тяжести 2. Выталкивающая сила Архимеда 3. Сила внутреннего трения, действующая на шарик радиуса r при его медленном поступательном движении со скоростью u и тормозящая движение шарика, которая определяется по формуле Стокса На основании второго закона Ньютона имеем:
Вначале скорость движения шарика возрастает
С этого момента движение шарика становится практически равномерным со скоростью
Скорость равномерного движения шарика Учитывая, что на опыте измеряется диаметр шарика, а не его радиус получаем расчетную формулу:
Порядок выполнения работы 1. По указанию преподавателя откройте программу, содержащую блок лабораторных работ по физике, раздел «механика, статистическая физика и термодинамика». Выберите нужную вам лабораторную работу. 2. Еще раз внимательно прочитайте теорию и методику проведения работы. Для этого щелкните левой клавишей на экране кнопку. «Теория и методика проведения работы». 3. Откройте flash - анимацию, для этого щелкните кнопку «Эксперимент». 4. Задайте параметры – вид жидкости, диаметр шарика, величину MN. 5. Щелкните кнопку «Пуск» для начала эксперимента. 6. Запишите параметры установки и время падения шарика в таблицу. 7. Повторите опыт 10 раз, изменяя параметры. 8. При помощи калькулятора произведите вычисления предлагаемых величин. 9. Сделайте вывод о проделанной работе. 10. Ответьте на контрольные вопросы.
Обработка результатов измерений
1. Коэффициент вязкости рассчитывается по формуле (5). 2. Относительную погрешность каждого опыта рассчитать по формуле
3. Абсолютную погрешность каждого опыта рассчитать по формуле
Таблица измерений
Контрольные вопросы: 1) Сформулируйте закон Архимеда. 2) Вследствие чего возникают силы внутреннего трения? Как они направлены? 3) Является ли сила сопротивления среды силой внутреннего трения? Обоснуйте ответ. 4) Напишите формулу Стокса. Дайте определения величин, входящих в формулу. 5) Какие силы действуют на шарик, падающий в жидкости? 6) На каком участке траектории падающего шарика результирующая сила изменяет своё значение с ростом скорости? 7) На каком участке траектории падающего шарика результирующая сила равна нулю? Каков характер движения шарика на этом участке? 8) Выведите единицу измерения h, используя расчётную формулу.
Лабораторная работа №6
Определение отношения молярных теплоемкостей газа СР ¤ СV методом адиабатического расширения
Цель работы: изучить термодинамические процессы в воздухе и определить отношение теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме методом адиабатического расширения (методом Клемана-Дезорма). Приборы и принадлежности: прибор Клемана-Дезорма. Теоретические сведения Теплоемкостью какого-либо вещества, называется физическая величина, численно равная количеству теплоты dQ, которое нужно сообщить телу, чтобы повысить его температуру на один градус: Теплоемкость единицы массы вещества называется удельной теплоемкостью, С Молярной теплоемкостьюназывается физическая величина, численно равная теплоте, которую нужно сообщить одному молю вещества при изменении его температуры на один кельвин в рассматриваемом термодинамическом процессе, С
Величина теплоемкости зависит от условий, при которых происходит нагревание вещества. Рассмотрим ……. В соответствии с первым началом термодинамики сообщение газу количества теплоты
· При изохорном нагревании объем газа V остается постоянным, где · При изобарном нагревании газа давление остается постоянным. Газ, расширяясь, совершает работу (для одного моля газа) Следовательно, Таким образом, теплоемкость при постоянном давлении
Отношение молярных теплоемкостей, является одной из важных термодинамических величин и называется показателем адиабаты (коэффициентом Пуассона)
Величина показателя адиабаты зависит только от числа степеней свободы газовых молекул: для одноатомных газов
для двухатомных газов (молекулы с жесткими связями)
для многоатомных газов (молекулы с жесткими связями)
В данной работе показатель адиабаты определяется для воздуха, который в основном состоит из двухатомных молекул О2, N2, … и с определенной погрешностью может быть описан с помощью уравнений используемых для идеального газа. В эксперименте реализуется адиабатно-изохорно-изотермический цикл. Циклом или круговым процессом называется совокупность термодинамических процессов, в результате которых система возвращается в первоначальное состояние. Адиабатическим называется термодинамический процесс, протекающий без теплообмена с окружающей средой. Уравнен
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.136 (0.009 с.) |

 , где Хmax-верхний предел измерений прибора;
-если класс точности К на панели прибора заключен в кружок:
, где Хmax-верхний предел измерений прибора;
-если класс точности К на панели прибора заключен в кружок:  , где Х-показание прибора.
, где Х-показание прибора.
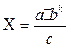 .
Рабочую формулу логарифмируют:
.
Рабочую формулу логарифмируют:  Затем дифференцируют:
Затем дифференцируют:
 .
Переходят от бесконечно малых к конечным и заменяют - на +, т.е.
.
Переходят от бесконечно малых к конечным и заменяют - на +, т.е.
 Окончательно получаем,
Окончательно получаем,
 .
.
 , затем рассчитывается погрешность каждого измерения
, затем рассчитывается погрешность каждого измерения  .
.



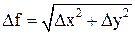




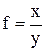


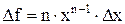

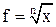








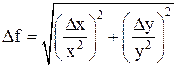
 .
.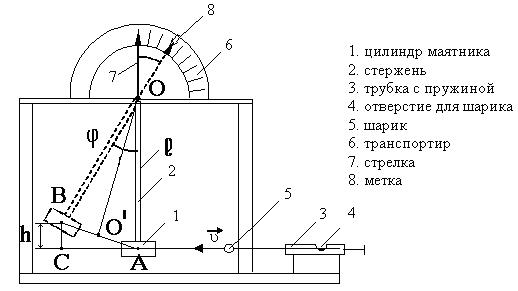
 с баллистическим маятником, в углублении цилиндра которого на месте контакта помещается слой неупругого материала - пластилина. При столкновении таких тел шарик застревает в пластилине и маятник вместе с ним движется как одно целое. При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим.
с баллистическим маятником, в углублении цилиндра которого на месте контакта помещается слой неупругого материала - пластилина. При столкновении таких тел шарик застревает в пластилине и маятник вместе с ним движется как одно целое. При ударе происходит изменение на конечные значения скоростей тел за очень короткий промежуток времени. При этом между сталкивающимися телами возникают кратковременные ударные силы, превосходящие во много раз все внешние силы, действующие на них. Поэтому такую систему соударяющихся тел в процессе удара можно рассматривать практически как замкнутую и применять для нее закон сохранения импульса. Если после столкновения тела движутся как одно целое, т.е. с одной и той же скоростью, то такой удар называют неупругим. , (1)
, (1) - скорость цилиндра маятника с шариком после удара; M – масса маятника; m – масса груза;
- скорость цилиндра маятника с шариком после удара; M – масса маятника; m – масса груза;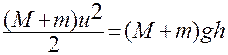 , (2)
, (2) . (3)
. (3) .
.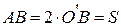 , т.е. равно смещению центра тяжести маятника, а OB=ℓ - расстоянию от точки подвеса до центра тяжести маятника. Поэтому для определения h получаем следующее выражение:
, т.е. равно смещению центра тяжести маятника, а OB=ℓ - расстоянию от точки подвеса до центра тяжести маятника. Поэтому для определения h получаем следующее выражение: . (4)
. (4) . (5)
. (5) . (6)
. (6) . (7)
. (7) , (8)
, (8)
 (1)
(1)
 (2)
(2)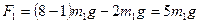 (здесь вычитается один из грузов слева, т.к. он предназначен для компенсации силы трения). Эта сила сообщит системе ускорение
(здесь вычитается один из грузов слева, т.к. он предназначен для компенсации силы трения). Эта сила сообщит системе ускорение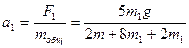 (3)
(3) (т.е. сила уменьшается в пять раз, а так как перегрузки переложили, а не убрали (добавили), то движущаяся масса не изменилась).
(т.е. сила уменьшается в пять раз, а так как перегрузки переложили, а не убрали (добавили), то движущаяся масса не изменилась). (4)
(4) (5),
(5),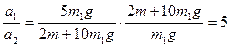 , т.о. соотношение (2) выполняется (при постоянной массе во сколько раз изменяется сила, во столько же раз изменяется и ускорение).
, т.о. соотношение (2) выполняется (при постоянной массе во сколько раз изменяется сила, во столько же раз изменяется и ускорение). , а
, а  .
.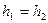 , то
, то 
 (6)
(6) .
.


 …
…
 …
…
 …
…

 в направлении внешней нормали n к поверхности слоя:
в направлении внешней нормали n к поверхности слоя: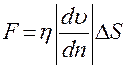 . (1)
. (1) (V - объем и ρ - плотность шарика)
(V - объем и ρ - плотность шарика) (ρ ’ – плотность жидкости)
(ρ ’ – плотность жидкости) .
.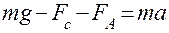 или
или  (2)
(2) , но так как по мере увеличения скорости сила сопротивления так же возрастает, то наступает такой момент, когда сила тяжести уравновешивается суммой сил Архимеда и Стокса и равнодействующая всех сил становится равной нулю.
, но так как по мере увеличения скорости сила сопротивления так же возрастает, то наступает такой момент, когда сила тяжести уравновешивается суммой сил Архимеда и Стокса и равнодействующая всех сил становится равной нулю. . (3)
. (3) . Решая уравнение движения относительно
. Решая уравнение движения относительно  , получим для коэффициента вязкости:
, получим для коэффициента вязкости: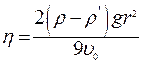 . (4)
. (4)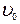 можно определить, зная расстояние ℓ между метками на сосуде и время t, за которое шарик проходит это расстояние
можно определить, зная расстояние ℓ между метками на сосуде и время t, за которое шарик проходит это расстояние  .
. . (5)
. (5) .
.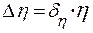 .
. .
.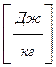 .
. .
. расходуется на увеличение внутренней энергии газа
расходуется на увеличение внутренней энергии газа 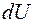 и совершением газом работы
и совершением газом работы 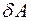 :
: .
. , и газ не совершает работу
, и газ не совершает работу  ; тогда
; тогда  и молярная теплоемкость при постоянном объеме определяется так:
и молярная теплоемкость при постоянном объеме определяется так:  ,
, - внутренняя энергия одного моля идеального газа, і - число степеней свободы молекулы газа.
- внутренняя энергия одного моля идеального газа, і - число степеней свободы молекулы газа.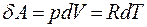 .
.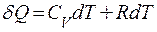 .
. .
. :
: .
. :
: ,
, :
: ,
, :
: .
.


