
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы.Содержание книги
Поиск на нашем сайте
Линейная зависимость и независ.строк м-цы.Расм.прямоуг.м-цы Аmxn l1=(a11,a12,a13,a14,..,a1n) – 1-я строка; l2=(a21,a22,a23,a24,..,a2n) – 2-я строка. lm=(am,am2,am3,am4,..,amn) Линейной комбинацией строк м-цы наз-ся выраж. λ– «лямбда». λ 1 * k1+ λ 2k2+… + λ m-1km -1+ λ mkm, где все λ -это числа. Опред.:строки l1,l2,..,lm – линейно независимые,если их линейная комбинация равна нулевой строке,когда все числа λ =0 (λ 1=0, λ 2=0, λ 3=0,.. λ m=0). Если опред-ль А не=0, то строки линейно независимы. Опр:строки l1,l2,l3,..lm-1,lm – лин.завис.,если их лин.комбинация = нулевой строке только, когда хотя бы одно из чисел λ 1, λ 2, λ m ≠0. ТЕОР.о ранге м-цы. Ранг м-цы равен максимальному числу её лин.независ.строк или ст-в м-цы, через которые линейно выражаются все остальные её строки (ст-цы). Пусть м-ца А размера mxn имеет ранг r(r≤min(m;n)). Это означает,что сущ-ет отличный от нуля минор r-го порядка. Всякий нулевой минор r-го порядка будет наз-ть базисным минором. Пусть для определённости это минор |a11 a12... a1r| |a21 a22... a2r| ∆= |... | ≠0. |ar1 ar2... arr| Тогда строки м-цы e1,e2,...,er линейно независимы. Предположим противное,т.е.одна из этих строк,напр. еr, явл-ся лин-й комбинацией остальных: er=λ1e1+λ2e2+...+λr-1er-1. Вычтем из эл-тов r-й строки эл-ты 1-й строки,умноженные на λ1, эл-ты 2-й строки, умноженные на λ2, и т.д., наконец,эл-ты (r-1)-й строки,умнож-е на λr-1. При таких преобразованиях м-цы её опред-ль ∆ не изм-ся, но т.к. теперь r-я строка будет состоять из одних нулей, то ∆=0 – противоречие, и наше предполож.неверно. 6. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений. 8. Система лин.ур-ний: Аmxn*Хnx1=Вmx1 <=> (ф.1) (a11x1+a12x2+…+ аnxn=b1 (a21x1+a21x2+… +a2nxn=b2 (…. (аmx1+а2mx2+… +аmnхn=bm В матричной форме система имеет вид АХ=В, где (а11 a12... a1n) A= (a21 a22... a2n) ф.2(............); (am1 am2.. amn) (x1) X= (x2) ф.3 (....); (xn) (b1) B= (b2) ф.4(....); (bm) называются собственно матрицей системы, матрицами-столбцами переменных и свободных членов. Решение системы:а) методом обр.м-цы. Ур-е в матричной ф-ме имеет вид АХ+В. Найти обр.м-цу. И найдём Х по ф-ле Х=А-1В,( т.е.х1,х2,х3.) б) По ф-ле Крамера. Найти определитель системы ^=|A|. Если он не=0,то сист.имеет единств.реш. Далее вычислить опред-ли м-ц ^ 1, ^ 2, ^ 3,полученных их м-цы А,заменой соотв-но 1-го,2-го и 3-го ст-цов столбцом своб.членов. Далее по ф-лам Крамера:х1= ^ 1/ ^, х2= ^ 2/ ^, х3= ^ 3/ ^.
Расширенной м-цей системы наз.м-ца (А|В),полученная из м-цы сист.А добавлением к ней ст-ца членов этой системы,т.е. (А|В)=(ф.2|ф.4) Теорема Кронекера-Капелли. Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы. r<m – ур-я с-мы(строки расш.м-цы)зависимые; r=m –ур-я с-мы (стр.расш.м.)независимые; r(A)не=r(A|B) - с-ма несовм-ная; r(A)=r(A|B)=r – с-ма совм-ная; r<n – с-ма неопред.(бескон.мн.реш.); r=n – с-ма опред-ная (единств.реш.) Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная. Если система лин.ур-й имеет единств.решение Х=(х1,х2,…хn),то такая сист.наз. определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист .не определённая. 7. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса. Метод Гаусса – метод послед-го исключ.переменных. Сначала(на 1-м шаге прямого хода Гаусса) из всех ур-ний,кроме 1-го исключается переменная х1. Потом (на 2 шаге) из всех ур-й,кроме первых 2-х исключается переменная х2 и т.д.,пока последнее ур-е не приобретёт вид: С * Хn=bm, если ч-ло С=0, а bm не=0,то с-ма не совместная,т.е.нет решений. Если С=0 и bm=0,т.е. 0*Хn=0,то с-ма неопределённая,т.е. имеет бескон.мн.реш.,то с-ма совместно-определённая. В этом сл-е Хn=bn/C Полученное зн-е Хn подстав.в предпосл.ур-е,находим Хn-1 и тд.,пока не получ.все неизв-е. Обратный ход Гаусса. Из м-цы ступенч.вида записывается ур-е. Далее,начиная с конца находим все переменные. Допустим Х4. Подставляем в верхнее и нах-м Х3 и т.д. Метод Гаусса — Жордана исп-ся для реш.квадр.систем лин.ур-ний, нахождения обрат.м-цы, отыскания ранга м-цы. Метод явл-ся модификацией метода Гаусса. Назван в честь Гаусса и Жордана. Теорема Кронекера-Капелли. Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы. r<m – ур-я с-мы(строки расш.м-цы)зависимые; r=m –ур-я с-мы (стр.расш.м.)независимые; r(A)не=r(A|B) - с-ма несовм-ная; r(A)=r(A|B)=r – с-ма совм-ная; r<n – с-ма неопред.(бескон.мн.реш.); r=n – с-ма опред-ная (единств.реш.) Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.
Если система лин.ур-й имеет единств.решение Х=(х1,х2,…хn),то такая сист.наз. определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист .не определённая. 8. Системы m линейных уравнений с n переменными.Теорема Кронекера-Капелли.Условие определённости и неопределённости любой системы линейных уравнений. Системы m линейных уравнений с n переменными имеет вид:
Произвольные числа, называемые соответственно коэффициентами при переменных и -свободными членами уравнений. при подстановке которых каждое уравнение системы обращается в верное равенство Теорема Кронекера-Капелли. Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы. r<m – ур-я с-мы(строки расш.м-цы)зависимые; r=m –ур-я с-мы (стр.расш.м.)независимые; r(A)не=r(A|B) - с-ма несовм-ная; r(A)=r(A|B)=r – с-ма совм-ная; r<n – с-ма неопред.(бескон.мн.реш.); r=n – с-ма опред-ная (единств.реш.) Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная. Если система лин.ур-й имеет единств.решение Х=(х1,х2,…хn),то такая сист.наз. определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист .не определённая. 9. Базисные(основные) и свободные(неосновные) переменные системы m линейных уранений с n переменными. Базисное решение.
10. Системы линейных однородных уравнений и её решения.Условия существования ненулевых решений системы. Системы линейных однородных уравнений. Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:
Систему (8) можно записать а виде: А*Х=0 (9). Если в системе (8) m=n, а ее определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю. Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r(A)<n.
11. Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами(сложение,умножение вектора на число).Коллинеарные и компланарные векторы. Если А — начало вектора и В — его конец, то вектор обозначается символом Обычно векторы обозначают одной малой латинской буквой со стрелкой либо выделяют жирным шрифтом:
Вектор изображается отрезком со стрелкой на конце: Длина вектора Вектор Вектор называется нулевым (обозначается Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Векторы Два вектора В этом случае пишут Все нулевые векторы считаются равными. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства (в частности, плоскости). Такой вектор называется свободным. Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. Вектор, противоположный вектору Для Векторы a1, a2,..., an называются компланарными, если каждый из них параллелен одной и той же плоскости. Любые два вектора всегда компланарны. Очевидно, если три вектора компланарны, то их можно изобразить направленными отрезками, лежащими в одной плоскости. Сумма векторов Пусть даны два вектора а = OA(вектор) и b = OB(вектор) (рис. 5).
От точки А отложим отрезок АС такой, что AС(вектор) = b. Тогда, вектор с = OС(вектор) называется суммой векторов а и b и обозначается а + b. Таким образом, OA(вектор) + AС(вектор) = OС(вектор). Это равенство называют правилом треугольника сложения двух векторов. Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а. Умножение вектора на число Произведением ненулевого вектора а на число х =/= 0 называется вектор, длина которого равна | x | • | а |, а направление совпадает с направлением а, если х > 0, и противоположно ему, если х < 0. Произведением нулевого вектора на любое число х и произведением любого вектора на число нуль называется нулевой вектор. Произведение вектора а на число х обозначается х • а (числовой множитель пишется слева). Согласно определению | x • а | = | x | • | а | для любого вектора а и любого числа х.
12. Скалярное произведение двух векторов(определение) и его выражениев координатной форме. Угол между векторами.
13. n-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.92.87 (0.011 с.) |






 , a.
, a.
 называется единичным.
называется единичным.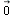 ), если начало и конец его совпадают.
), если начало и конец его совпадают. , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой вектор коллинеарен любому вектору.
, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой вектор коллинеарен любому вектору.
 .
. .
.





