
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение стандартной энтальпии реакции нейтрализации.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Цель: научиться экспериментально определять изменение энтальпии реакции. Задание: определить стандартную энтальпию реакции нейтрализации азотной кислоты гидроксидом натрия. Оборудование: калориметр, мерные цилиндры, термометр, воронка. Реактивы: растворы азотной кислоты и гидроксида натрия. Сущность работы: теплота реакции нейтрализации определяется калориметрически по измеренному изменению температуры и рассчитанной теплоемкости системы.
Лабораторный калориметр:
1 – внешний стакан, 2 – внутренний стакан, 3 – раствор, 4 – воронка, 5 – термометр.
Энтальпия реакции нейтрализации, протекающей между сильными одноосновными кислотами и сильными однокислотными основаниями практически не зависит от их природы, так как реально в растворах протекает одна и та же реакция: Н+(aq) + ОН–(aq) = Н2О(ж); DН°r = -57,3 кДж/моль. В случае реакции нейтрализации слабых кислот и слабых оснований такого постоянства не наблюдается, так как часть теплоты расходуется на ионизацию слабой кислоты и слабого основания. Выполнение эксперимента: 1. Подготавливают калориметр к работе. (Осматривают его, чтобы убедиться в исправности всех деталей. Ополаскивают дистиллированной водой внутренний стакан). 2. Мерными цилиндрами отмеривают равные объемы растворов кислоты и основания (20 – 25 мл, по указанию преподавателя). 3. Измеряют начальные температуры кислоты и щелочи с помощью термометра. 4. Раствор кислоты переливают при помощи воронки во внутренний стакан калориметра. 5. Раствор щелочи быстро вливают в калориметр к раствору кислоты и наблюдают за столбиком ртути термометра. Записывают самое высокое показание. Опыт повторяют 2 - 3 раза.
Масса внутреннего стакана калориметра, m (стакана) = ______ г Объемы растворов реагирующих веществ, V(HNO3) = _______ мл, V(NaOH) = _______ мл Концентрация растворов, c(HNO3) = _____ моль/л, c(NaOH) = _______ моль/л Плотность растворов, ρ(HNO3) = _______ г/мл, ρ(NaOH) = _______ г/мл Удельная теплоемкость растворов (воды), Cm(H2O) = 4,184 Дж/(г∙К) Удельная теплоемкость стекла, Сm(ст.) = 0,753 Дж/(г∙К)
Обработка результатов эксперимента: Для вычисления по экспериментальным данным теплоты реакций нейтрализации сначала рассчитывают общую теплоемкость калориметра Сm, учитывая теплоемкость раствора и теплоемкость внутреннего стакана:
Сm = Cm(H2O) ∙ m(раствора) + Сm(ст.) ∙ m(стакана)
где: m(раствора) = V(HNO3) ∙ ρ(HNO3) + V(NaOH) ∙ ρ(NaOH)
Затем вычисляют выделившуюся в калориметре теплоту: Q = Cm ∙ ΔT
где: ΔT = t(после нейтрализации) – Эта теплота постепенно, по мере выравнивания температуры передается в окружающую среду и может быть принята равной по абсолютной величине изменению энтальпии системы (калориметра): ΔnH = -Q
Для расчета стандартной энтальпии реакции нейтрализации найденное значение теплоты необходимо пересчитать на 1 моль реагирующей кислоты или основания, что соответствует 1 моль образующейся воды: ΔnH° = где: ν – количество вещества кислоты или щелочи (в зависимости от того, что находится в недостатке).
ν(HNO3) = V(HNO3) ∙ c(HNO3), или ν(NaOH) = V(NaOH) ∙ c(NaOH)
Рассчитанную стандартную энтальпию реакции нейтрализации сравнивают со справочными данными. Рассчитывают отклонение найденных значений от справочных. Объясняют вероятные причины отклонений.
Расчеты: 1) t01 = 2) ∆t0 = t2 – t1 =
3) Cр-ра = C0m(H2O)
4) V1 р-ра = Vк.
5) Сстак. = С0стак. mстак. =
6) Ссистемы = Сстак. + Cр-ра =
7) ∆H = -Q = -Ссист.
8) ν = Ск.
9) ∆nH0эксп. = Относительная ошибка: εотн.= ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Вывод (указывают полученный результат, метод исследования, относительную ошибку): _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Занятие ___. Дата ____.____. 20 ___
Тема: Химическая кинетика. Теоретический материал к занятию:
Химическая кинетика изучает скорости химических реакций, их зависимость от различных факторов и механизмы реакций. Последовательность и характер стадий химических реакций называют механизмом реакции. По механизму различают простые и сложные реакции. Простые реакции осуществляются посредством однотипных элементарных актов. Под элементарным актом понимают единичный акт взаимодействия или превращения частиц, в результате которого образуются новые частицы продуктов реакции или промежуточных соединений. В элементарном акте принимает участие одна или две частицы (описаны единичные случаи одновременного взаимодействия трех частиц). Для осуществления сложных реакций необходимы разнотипные (не менее двух) элементарные акты. Различают следующие типы сложных реакций: параллельные, последовательные, сопряженные, цепные. Для параллельных реакций характерно протекание нескольких процессов с участием одних и тех же исходных веществ. Эти процессы завершаются образованием разных продуктов реакции. Скорость параллельных реакций определяется наиболее быстрой стадией В последовательных реакциях образование конечного продукта реакции из исходных веществ происходит не непосредственно, а обязательно через ряд промежуточных продуктов. Скорость последовательной реакции определяется наиболее медленной стадией, которая называется лимитирующей стадией. Некоторые сложные реакции состоят как из последовательных, так и параллельных реакций. Скорость химической реакции (v) определяется изменением концентрации Δс реагирующих веществ (или продуктов реакции) в единицу времени. Размерность скорости химической реакции — концентрация/время: dim v = L-3T-1N, наиболее употребляемая единица измерения — моль на литр-секунду [моль/(л∙с)]. Скорость химической реакции в общем случае не является постоянной в течение всего времени ее протекания. Рассмотрим обратимую реакцию: аА+ bB ↔ dD + fF Скорость прямой реакции (образование веществ D и F) уменьшается по мере расходования исходных веществ (А и В), а скорость обратной реакции будет увеличиваться по мере накопления продуктов реакции (D и F). В связи с этим в химической кинетике пользуются понятием средней скорости в данном интервале времени Δ t: Δc vср = ± —— Δt Истинная скорость (в любой момент времени) определяется первой производной концентрации по времени: dc vист= ± —— dt Скорость химической реакции зависит в первую очередь от природы реагирующих веществ. Скорость гомогенной реакции зависит от концентрации реагентов, а гетерогенных — от площади соприкасающихся фаз, т. е. степени дисперсности. Скорости всех реакций зависят от температуры, многих реакций — от присутствия катализаторов. Зависимость скорости химической реакции от концентрации описывается кинетическим уравнением. Например, для реакции: аА+ bB ↔ продукты v = kcp(A)cq(B) где p, q — эмпирические (найденные экспериментальным путем) коэффициенты, не обязательно совпадающие со стехиометрическими коэффициентами а и b; k - константа скорости реакции, размерность которой зависит от значений p и q. Константа скорости зависит от тех же факторов, что и скорость химической реакции, но не зависит от концентрации реагирующих веществ. Величина р +q определяет порядок кинетического уравнения реакции, который показывает, каким образом скорость реакции зависит от концентрации реагентов. Порядок кинетического уравнения может принимать значения 0, 1, 2 и более, он может быть также дробным. Важной характеристикой реакции является период полупревращения t0,5 — время, за которое в реакцию вступает половина исходного вещества. Для радионуклидов аналогичная величина называется периодом полураспада. Кинетические расчеты позволяют ответить на следующие вопросы: 1) сколько времени требуется для уменьшения концентрации исходного вещества до заданного уровня? (Так, например, можно определить оптимальные промежутки времени между приемами лекарственного средства); 2) какой будет концентрация исходного вещества по истечении заданного промежутка времени? (Так оценивается, например, остаточное количество токсиканта.) Для решения этих вопросов используют кинетические уравнения. Обозначим через cо начальную концентрацию реагента, через ct — концентрацию реагента в момент времени t. Для реакций нулевого порядка: dc - —— = k dt откуда c0 — ct = kt c0 t0,5 = — 2k dim k = L-3T-1N, единица измерения—моль на литр-секунду [моль/(л∙с)]. _____________________________________________________________________________________________
Для реакций первого порядка: dc - —— = kt dt c0 откуда ln — = kt ct ln2 0,69 t0,5 = — = —— k k dim k = T-1, единица измерения—секунда в минус первой степени (с-1). _____________________________________________________________________________________________
Для реакций второго порядка: dc - —— = kc2 dt 1 1 Откуда — - — = kt c0 ct t0,5 = —— c0k dim k = L3T-1N-1; единица измерения—литр на моль-секунду [л/(моль∙с)]. _____________________________________________________________________________________________
Из приведенных уравнений можно сделать следующие выводы: 1) величина константы скорости уравнения первого порядка не зависит от способа выражения концентрации, а констант нулевого и второго порядков зависит. Например, если концентрацию выразить не в моль на литр, а в миллимоль на литр, то величина константы скорости кинетических уравнений нулевого порядка увеличится в 1000 раз, а величина константы скорости кинетических уравнений второго порядка в 1000 раз уменьшится; 2) величины констант скорости кинетических уравнений всех порядков зависят от выбранной единицы времени. Например, если время выразить не в секундах, а в минутах, то величины констант возрастут в 60 раз; 3) период полупревращения реакций первого порядка не зависит от начальной концентрации реагента, период полупревращения реакций нулевого порядка возрастает при увеличении со, а реакций второго порядка уменьшается. Анализируя зависимость периода полупревращения реакции от начальной концентрации реагента, можно определить порядок реакции. Скорость реакций зависит от температуры. В соответствии с эмпирическим правилом Вант -Гоффа скорость большинства реакций увеличивается приблизительно в 2 - 4 раза при увеличении температуры на 10 °С:
kT+ΔT = kTγΔT/10 где γ — температурный коэффициент константы скорости реакции.
Многие каталитические реакции не подчиняются этому правилу, для большинства из них γ < 2. Почти все биохимические реакции осуществимы только в присутствии ферментов, следовательно, почти все они не подчиняются данному правилу. Кроме того, при увеличении температуры свыше определенного значения (45 - 50 °С) биохимические реакции резко замедляются, а затем останавливаются, что связано с инактивацией ферментов при высоких температурах. Более точную зависимость скорости химической реакции от температуры устанавливает уравнение Аррениуса: k = k0e-Ea /RT где Еа – энергия активации реакции; k0 – предэкспоненциальный множитель, пропорциональный числу столкновений реагирующих частиц. Энергия активации реакции Еа - энергетический барьер, который должны преодолеть исходные вещества по пути превращения в продукты реакции (рис. 3-1). Dim Ea = L2MT-2N; единица измерения— джоуль на моль (Дж/моль).
Уравнение Аррениуса для двух температур имеет следующий вид: k 2 Ea ln ¾¾ = ¾¾ (1/T1- 1/Т2) k1 R
или
k 2 Ea Δ T ln ¾¾ = ¾¾¾¾ k1 R T1Т2 где k1 и k2 – константы скорости при температурах T1 и T2, соответственно.
Скорость многих реакций зависит от присутствия веществ, не расходующихся в ходе реакции; такие реакции называются каталитическими. Под катализом понимают изменение скорости химических реакций в присутствии веществ, которые после завершения реакции остаются в неизменном виде и количестве. Увеличение скорости реакции называют положительным катализом, уменьшение — отрицательным катализом, или ингибированием. Катализаторами называют вещества, которые вызывают положительный катализ; вещества, замедляющие реакции, называют ингибиторами. Катализатор ускоряет только термодинамически возможную реакцию, причем ускоряет как прямую, так и обратную реакции. Таким образом, катализатор ускоряет достижение состояния химического равновесия в системе, не смещая положение равновесия. Механизм действия катализатора заключается в изменении пути процесса превращения реагентов в продукты. Новый путь характеризуется меньшим энергетическим барьером, т. е. меньшей энергией активации. Величина ΔЕа служит критерием эффективности катализатора. Если условно принять, что величины предэкспоненциальных множителей каталитической и некаталитической реакций одинаковы (на самом деле они отличаются), то в соответствии с уравнением Аррениуса получим следующее уравнение: k’ ΔEa = RT ln— k
где k’ и k — константы скорости каталитической и некаталитической реакций соответственно. Это уравнение можно использовать для приблизительной оценки изменения скорости реакции при введении в систему катализатора.
Перед решением задач рекомендуется выучить следующие основные понятия темы: 1) скорость химической реакции; 2) константа скорости химической реакции; 3) период полупревращения и период полураспада; 4) порядок и молекулярность реакции; 5) температурный коэффициент скорости реакции; 6) энергия активации.
Уметь применять: 1) кинетические уравнения химических реакций разного порядка; 2) зависимость константы скорости химической реакции от различных факторов; 3) методы определения значения энергии активации; 4) математическое выражение правила Вант-Гоффа; 5) уравнение Аррениуса; 6) связь между энтальпией реакции и энергией активации прямой и обратной реакций.
Обратить внимание на то, что: 1) порядок реакции определяют, сопоставляя изменение величин начальной концентрации (со) и периода полупревращения (t0,5). Реакции, для которых наблюдается прямая зависимость между изменениями значений со и t 0,5, относятся к реакциям нулевого порядка; реакции с обратной зависимостью величин со и t 0,5 - к реакциям второго порядка; реакции, в которых t 0,5 2) единицы измерения константы скорости зависят от порядка кинетического уравнения реакции; 3) для реакций первого порядка молярные концентрации могут быть заменены любым другим способом выражения состава системы (массовая доля, массовая концентрация и др.), но обязательно одинаковыми для со и сt; 4) единицы измерения величин Еа и произведения RT, входящих в уравнение Аррениуса: k = А×е-Еа/RT, должны совпадать, т.к. их отношение стоит в показателе степени и должно быть безразмерной величиной; 5) приращение температур Dt = t2- t1(DТ = Т2- Т1) в математическом выражении правила Вант-Гоффа: v 2= v 1× или k 2= k 1× может иметь единицы измерения как в °С, так и в К, и следовательно, 10, стоящая в знаменателе показателя степени температурного коэффициента γ, тоже может иметь единицы измерения либо в °С, либо в К. 7) В уравнении: k 2 Ea ln ¾¾ = ¾¾ (1/T1- 1/Т2) k1 R единицы измерения величины Еа должны быть Дж/моль, т.к. единицы измерения газовой постоянной R - Дж/(моль× К) и в левой части уравнения стоит безразмерная величина k 2/k 1.
Учесть, что можно рассчитать: 1) энергию активации Еа, если известны значения k1, k2; 2) константу скорости химической реакции при любой температуре; 3) такие кинетические характеристики, как температурный коэффициент Вант-Гоффа, период полупревращения.
Примеры решения типовых задач Пример 1 . Определение порядка реакций по кинетическим данным Определите порядок реакции NH4CNO исходя из следующих данных: Исходная концентрация, со моль/л 0,10 0,20 0,40 Период полупревращения, t 0,5, час 19,15 9,45 4,62 Решение. Анализ приведенных данных показывает, что с увеличением исходной концентрации период полупревращения уменьшается, такой характер зависимости свойственен реакциям второго порядка. Ответ: реакция второго порядка.
Пример 2 . Расчет скорости реакции по константе скорости и концентрации. Константа скорости реакции Н2(г) + I2(г) В сосуд объемом 2 л ввели по 2 моль водорода и иода. Чему будет равна скорость реакции в тот момент, когда в реакционной смеси образуется 0,2 моль иодоводорода? Решение. По условию задачи константа скорости реакции имеет единицы измерения [концентрация-1× время-1]. Следовательно, реакция образования газообразного иодоводорода из простых веществ является реакцией второго порядка. Кинетическое уравнение скорости реакции второго порядка имеет вид:
Исходя из уравнения реакции, определим количество каждого реагента, необходимое для образования 0,2 моль иодоводорода. Рассчитаем количество исходных реагентов, оставшееся к моменту времени, когда в реакционной смеси образуется 0,2 моль НI. n(Н2)вст=n(I2)вст=0,5× n (НI)обр=0,1 моль. n(Н2)ост=n(I2)ост=2 – 0,1=1,9 моль. с(Н2)=с(I2)= 1,9:2=0,95 моль/л
Рассчитаем скорость реакции: v = 0,111 л/(моль·с)·0,952 моль2/л2 = 0,1 моль/(л·с) Ответ: 0,1 моль/(л·с).
Пример 3 Расчет периода превращения по кинетическому уравнению первого порядка. Концентрация пестицида диурона в пробе воды с pH 7,0 была равна 0,07 ммоль/л. Через 2,5 месяца она стала вследствие протекающего гидролиза равна 0,05 ммоль/л. Вычислите период полупревращения реакции гидролиза диурона. Температура пробы поддерживалась постоянной (18 °С). Решение. При решении задачи основным является уравнение для константы скорости химической реакции первого порядка, записанное в виде: 1 cо k = ¾¾ ln ¾¾ t c t Вычислив значение k по уравнению, определим период полупревращения вещества по формуле (3.2): 0,69 t 0,5 = ¾¾ k Подставляя в выражение приведенные в условии задачи значения, вычислим: 1 0,07 ммоль/л k = ¾¾¾ ln ¾¾¾¾¾¾ = 0,135 мес-1. 2,5 мес 0,05 ммоль/л
Тогда из выражения: 0,69 t 0,5 = ¾¾¾¾ = 5,1 мес. 0,135 мес-1 Ответ: 5,1 месяцев.
Пример 4 Расчет времени, необходимого для достижения заданной концентрации и концентрации реагента в заданный момент времени по кинетическому уравнению первого порядка. Для проведения исследований были взяты равные массы двух радионуклидов: 137Cs и 95Zr. Какая часть радионуклида 137Cs останется к тому моменту, когда 99% радионуклида 95Zr подвергнется распаду. Решение. Для радионуклидов время, за которое в реакцию вступает половина исходного вещества, называется периодом полураспада(t0,5).При решении задачи воспользуемся уравнением для константы скорости химической реакции первого порядка, т.к. радиоактивный распад протекает по первому порядку: 1 cо k = ¾¾ ln ¾¾ t c t Из уравнения (3.1) выразим: 1 cо t = ¾¾ ln ¾¾ k c t где t0,5 - время, за которое распадается 99% радионуклида 95Zr. Исходя из формулы, определим константу скорости химической реакции: 0,69 k = ¾¾ t 0,5 где t 0,5 - период полураспада 95 Zr (справочная величина, табл. 04.01) Вычислим, какая часть радионуклида 137Cs останется к тому моменту, когда 99% 95Zr подвергнется распаду. По справочным данным t 0,5 (95Zr) = 64 сут.; t 0,5 (137Cs) = 30,17 года (табл. 04.01) 0,69 k (95Zr) = ¾¾¾ = 1,1·10-2 сут-1 64 сут-1
0,69 k (137Cs) = ¾¾¾ = 0,023 года-1 30,17 года-1 Вычислим величину t, зная значение k (95Zr): 1 100% t = ¾¾¾¾ ln ¾¾¾ = 419 сут = 1,15 года 1×10-2 сут-1 1% Применяя уравнение в экспоненциальной форме, находим: cо (137Cs) kt ¾¾¾¾¾ = e c t(137Cs)
cо (137Cs) ¾¾¾¾¾ = e 0,023 года-1×115 года = 1,03 c t(137Cs)
c t(137Cs) = 0,97 или 97%. Ответ: останется 97 %.
Пример 5 Расчет по кинетическому уравнению первого порядка: - времени, необходимого для достижения заданной концентрации; - концентрации реагентов в заданный момент времени; - периода превращения. Константа скорости гидролиза сахарозы при 25 °С равна 3,2 ×10-3 час-1. Рассчитайте: а) время, за которое гидролизу подвергнется 10% исходного количества сахарозы; б) какая часть сахарозы подвергнется гидролизу через 5 суток; в) период полупревращения реакции. Решение. Рассматриваемая реакция является реакцией первого порядка, т.к. константа имеет единицы измерения [время-1]. Обозначим исходную массу сахарозы mо, а конечную массу - mt. К моменту времени t подвергнется гидролизу 0,1m cахарозы. Тогда к моменту времени t останется mt = m – 0,1m = 0,9m; Для ответа на вопрос а) воспользуемся модифицированым уравнением: mо ln ¾¾ = kt mt Выразим и вычислим величину t из этого уравнения: 1 mо 1 0,1m t = ¾¾ ln ¾¾ = ¾¾¾¾¾¾ ln ¾¾¾ = 32,9 ч. k mt 3,2 × 10-3час-1 0,9m
Для ответа на вопрос б) преобразуем ln mо - ln mt = kt; откуда mо ln ¾¾¾ = 3,2 ×10-3час-1× 120 час mt
mо ln ¾¾¾ = 0,384 mt mо/mt = е0,384 или mо/mt = 1,47 откуда mt = mо/1,47 = 0,68 m, т.е. за 5 суток в реакцию вступит m – 0,68m = 0,32m сахарозы, т.е. 32% от исходной массы сахарозы.
Период полупревращения (вопрос с) рассчитаем по: ln 2 0,69 t 0,5 = ¾¾¾ = ¾¾¾¾¾¾¾ = 216 час. k 3, 2 × 10-3час-1 Ответ: 32,9 час., 32 % сахарозы, 216 час. Пример 6 Расчет времени и константы скорости при второй температуре с использованием энергии активации и кинетических параметров при первой температуре. Разложение спазмолитина в растворе является реакцией первого порядка с энергией активации 75 кДж/моль. Период полупревращения при 20 °С равен 103 часам. Рассчитайте время, за которое разложится 25% спазмолитина при 37 °С. Решение. Пусть t1 = 200С, а t2 = 370С, т.е. Т1= 293К и Т2 = 310 К. Рассчитаем константу скорости k1 при Т1= 293К, воспользовавшись (3.2): 0,69 0,69 k1 = ¾¾ = ¾¾¾¾ = 6,70 × 10-3 час-1 t0,5 103 час Для расчета константы скорости k2 при Т2 = 310 К воспользуемся уравнением Аррениуса для двух температур(3.5). Сначала вычислим значение ln k2/ k1: k2 75 кДж/моль × 17 К ln ¾ = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = 1,69 k1 8,31× 10-3 кДж/(моль×К) ×293К× 310 К Откуда k2/ k1 = е1,69 = 5,42 и k2 = 5,42 × 6,7 ×10-3 = 3,63 ×10-2 час-1 Рассчитаем время, за которое разложится 25% спазмолитина при 370С: t = ¾¾¾ × ln(100/75) = 7,93 час»8 час. Ответ: 8 час.
Пример 7 Расчет энергии активации по кинетическим данным при разных температурах. Периоды полупревращения денатурации некоторого вируса равны: при 30 °С 5 час., при 37 °С - 1,76·10-2 часа. Денатурация описывается кинетическим уравнением первого порядка. Вычислите энергию активации процесса. Решение. Известно, что для реакций первого порядка значение константы k обратно пропорционально t0,5, поэтому уравнение Аррениуса для двух температур (3.5) можно представить следующим образом: t0,5 1 EaDТ ln ¾¾¾ = ¾¾¾¾ t0,5 2 Т1Т2 Преобразуем это выражение относительно Ea: R Т1Т2 t0,5 1 Ea = ¾¾¾ln ¾¾ DТ t0,5 2 Подставим в это выражение известные по условию задачи величины: 8,31× 10-3 кДж/(моль × К) × 303 К × 310 К 5 час Ea = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ ln ¾¾¾¾¾¾ = 630 кДж/моль 7К 1,76× 10-2 час Ответ: 630 кДж/моль.
Пример 8 . Расчет энергии активации по температурному коэффициенту скорости реакции. Вычислить энергию активации гидролиза этилацетата в щелочном растворе (10 °С - 45 °С); Решение. Зависимость константы скорости химической реакции от температуры выражается приближенным правилом Вант-Гоффа: k2/k1= Представим уравнение Вант-Гоффа в логарифмической форме: t2-t1 ln k2/k1=¾¾¾ lng
Выведем расчетную формулу для энергии активации, используя (3.3) и (3.5): R×T1×T2×ln g Еа = ¾¾¾¾ Подставив в полученное выражение известные по условию задачи значения, вычислим: 8,31Дж/(моль ×К) ×283 К ×318 К× ln1,9 Еа = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = 48001 Дж/моль Ответ:
Пример 9 . Расчет температурного коэффициента скорости реакции по энергии активации Вычислите температурный коэффициент скорости реакции. Разложения пероксида водорода (25 °С - 55 °С), Еа = 75,4 кДж/моль. Решение: Температурный коэффициент рассчитаем по формуле, используя (3.3) и (3.6):
Подставляя известные по условию задачи значения в это уравнение, вычислим:
Анализ полученного ответа: Значение
Пример 10 .Сравнение констант скорости каталитической и некаталитической реакции с использованием значений энергии активации. Оцените, во сколько раз возрастет скорость реакции разложения угольной кислоты при 310 К, если в присутствии карбоангидразы Еа = 49 кДж/моль, а без катализатора Еа = 86 кДж/моль. Решение. Для того, чтобы оценить эффективность работы катализатора, можно использовать выражение(3.6): k кат DЕа ln ¾¾¾ = ¾¾¾ k без кат RT Ответим на поставленный вопрос, подставив известные по условия задачи величины: k кат (86000 – 49000) Дж/моль ln ¾¾¾ = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = 1,73×106 k без кат 8,31 Дж/(моль·К)·310 К
Ответ: Катализатор увеличивает константу скорости в 1,73×106 раз.
Пример 11 Расчет периода полупревращения по кинетическим данным при разных температурах. Период полупревращения некоторой реакции первого порядка равен 15,4 час при 298 К. Как изменится период полупревращения при введении катализатора, снижающего энергию активации на 15000 Дж/моль? Решение. При введении катализатора в реакционную смесь значение константы скорости увеличивается, а значение периода полупревращения уменьшается. Выразим отношение каталитической и некаталитической реакции: k кат t0,5 без кат ¾¾¾ = ¾¾¾¾¾ k без кат t0,5 кат Преобразуем данное уравнение с учетом (3.6): t0,5 без кат DЕа ln ¾¾¾¾¾ = ¾¾¾¾ t0,5 кат RT Отсюда t0,5 кат = t0,5 без кат/ еDЕа/R×T t0,5 кат = 15,4час/ е 15000 Дж/моль:{8,31 Дж/(моль×К) ×298К} k кат/ k без кат = 15,4 час: 0,036 час = 427,7 Ответ: введение катализатора снижает период полупревращения реакции в 428 раза.
Пример 12 Энергетические профили реакций. Для прямой реакции Еа = 80 кДж/моль; DrН° = 25 кДж/моль. Чему равны энергия активации и стандартная энтальпия обратной реакции? Решение. Учитывая, что прямая реакция является эндотермической ( DrН°(прям) = Еа(прям) -Еа(обрат) или Еа (обрат) = Еа(прям) - Тогда Еа (обрат) = 80 кДж/моль - 25 к Дж/моль = 55 кДж/моль DrН°(обрат) = -25 кДж/моль Ответ: Еа(обрат) = 55 кДж/моль; DrН°(обрат) = -25 кДж/моль
Занятие ___. Дата ____.____. 20 ___
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |


 Экспериментальные данные:
Экспериментальные данные:
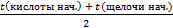

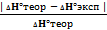

 =
= mр-ра =
mр-ра = ρк. + Vщ.
ρк. + Vщ.  =
=

 f (со) - к реакциям первого порядка;
f (со) - к реакциям первого порядка; t2-t1/10
t2-t1/10 (NH2)2CO,
(NH2)2CO, 2НI(г) при 714 К 0,111 л/(моль×с).
2НI(г) при 714 К 0,111 л/(моль×с). 48 кДж/моль
48 кДж/моль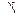 = e 10Еа/RT1Т2
= e 10Еа/RT1Т2 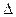 rН° пр. > 0).
rН° пр. > 0).


