
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания систем с двумя степенями свободы. Порядок расчета.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Перемещения масс
или Наличие в уравнениях свободных членов вида
Тогда Подставим полученные выражения производных и перемещений в уравнения (1) и сократим на
или Преобразуем систему уравнений к такому виду:
Каждую максимальную амплитуду Максимальные силы инерции определяются при
Подставляя в (2) вместо
Решая эти уравнения при известной частоте возмущений нагрузки, получаем значения максимальных инерционных сил. В случае, когда частота возмущающей нагрузки Зная максимальные силы инерции, можно определить все внутренние усилия в системе в состоянии наибольших отклонений.
где
31.Метод Релея определения частот свободных колебаний. Во время свободных колебаний происходит переход кинетической энергии системы в потенциальную, и наоборот. Если пренебрегать сопротивлениями, то по закону сохранения энергии можно написать
где В момент перехода массы через положение статического равновесия потенциальная энергия деформации равна нулю, а кинетическая достигает небольшого значения Так как минимальные значения потенциальной кинетической энергии равны нулю, то из (1) можно сделать вывод, что
Это уравнение при подстановке в него выражений энергии дает возможность определить частоты колебаний. Для приближенного решения необходимо задать динамическую упругую линию уравнением
Для определения максимальной кинетической энергии необходимо найти наибольшее значение скорости
Кинетическая энергия будет равна
Предполагаем, что масса распределена по стержням по определенному закону. Максимальное значение кинетической энергии соответствует случаю когда
Величина потенциальной энергии деформации для изгибаемых систем выражается зависимостью
Тогда
Подставляем полученные значения в (2), находим
Иногда бывает удобнее числитель в (3) заменить удвоенной работой внутренних сил или удвоенной работой статических внешних сил
или
Если кроме масс на систему действуют сосредоточенные внешние нагрузки, точки приложения которых смещаются на величины
Как видно из формул (3) – (6), значение частоты свободных колебаний по этому методу зависит от того, насколько точно задано уравнение упругой линии. При задании истинной формой колебаний эти формулы дают точные значения низших частот. Следует заметить, что при приближенном задании формой упругой линии значения частот получаются всегда преувеличенными против точных значений.
32.Метод Граммеля определения частот свободных колебаний. Этот метод, как и метод Релея, основан на равенстве максимальных значений потенциальной и кинетической энергии. Пусть
где Изгибающие моменты, вызываемые силами инерции
Обозначим
и Наибольшая кинетическая энергия, которая развивается в процессе колебаний, будет равна, как и по методу Релея:
Приравнивая выражения (7) и (8), приходим к формуле Граммеля:
Для вычисления частоты по этой формуле, необходимо, прежде всего, задаться подходящей формой упругой линии
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.007 с.) |

 Пусть на упругую балку с двумя сосредоточенными массами действует периодическая возмущающая нагрузка гармонического типа
Пусть на упругую балку с двумя сосредоточенными массами действует периодическая возмущающая нагрузка гармонического типа  (рис. 3). Основная задача расчета заключается в определении максимальных внутренних усилий и перемещений в балке и проверка на резонанс.
(рис. 3). Основная задача расчета заключается в определении максимальных внутренних усилий и перемещений в балке и проверка на резонанс. и
и  от действия инерционных сил и возмущающей нагрузки выражаются следующими зависимостями:
от действия инерционных сил и возмущающей нагрузки выражаются следующими зависимостями:
 .
. . (1)
. (1) ;
;  .
. ;
;  .
. .
.
 .
. (2)
(2) и
и  можно представить как результат действия максимальных сил инерции
можно представить как результат действия максимальных сил инерции  и
и  и амплитудного значения возмущающей нагрузки
и амплитудного значения возмущающей нагрузки  .
. , т.е.
, т.е. ,
, .
.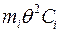 величины
величины 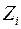 , получаем систему канонических уравнений для определения максимальных сил инерции.
, получаем систему канонических уравнений для определения максимальных сил инерции. .
. совпадает с одной из частот собственных колебаний, наступает явление резонанса.
совпадает с одной из частот собственных колебаний, наступает явление резонанса. ;
; ;
;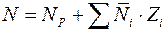 ,
, ,
, 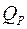 ,
,  – внутренние усилия в системе от действия амплитудного значения возмущающей нагрузки;
– внутренние усилия в системе от действия амплитудного значения возмущающей нагрузки;  ,
,  ,
,  – усилия в системе от единичных сил, приложенных по направлению сил инерции.
– усилия в системе от единичных сил, приложенных по направлению сил инерции. , (1)
, (1) – кинетическая энергия и
– кинетическая энергия и  – потенциальная.
– потенциальная. . В момент наибольшего отклонения кинетическая энергия равна нулю, а потенциальная энергия достигает максимума
. В момент наибольшего отклонения кинетическая энергия равна нулю, а потенциальная энергия достигает максимума  .
. (2)
(2) удовлетворяющим граничным условиям, например, уравнением изогнутой оси стержня при действии на него статической нагрузки, соответствующей приложенным массам. Предположим, что уравнение изогнутой оси имеет такой вид:
удовлетворяющим граничным условиям, например, уравнением изогнутой оси стержня при действии на него статической нагрузки, соответствующей приложенным массам. Предположим, что уравнение изогнутой оси имеет такой вид: .
. .
.

 .
.
 .
.

 (3)
(3) (4)
(4) (5)
(5) , то в формулу (5) добавится слагаемое в числителе:
, то в формулу (5) добавится слагаемое в числителе: (6)
(6) задаваемая форма свободных колебаний стержня. Тогда интенсивность максимальных сил инерции определяется выражением
задаваемая форма свободных колебаний стержня. Тогда интенсивность максимальных сил инерции определяется выражением ,
, – интенсивность распределенной массы.
– интенсивность распределенной массы. . Тогда выражение максимальной потенциальной энергии деформаций будет иметь вид:
. Тогда выражение максимальной потенциальной энергии деформаций будет иметь вид:
 – изгибающий момент, вызываемый условной нагрузкой
– изгибающий момент, вызываемый условной нагрузкой  ,т.е. нагрузкой в
,т.е. нагрузкой в  раз меньше, чем силы инерции. Тогда
раз меньше, чем силы инерции. Тогда
 (7)
(7)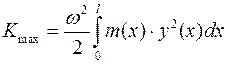 (8)
(8)
 . После этого путем умножения
. После этого путем умножения  . Теперь остается вычислить выражения, входящие в числитель и знаменатель (9). Следует отметить, что при задании одной и той же формы упругой линии, формула Граммеля оказывается точнее формулы Релея.
. Теперь остается вычислить выражения, входящие в числитель и знаменатель (9). Следует отметить, что при задании одной и той же формы упругой линии, формула Граммеля оказывается точнее формулы Релея.


