
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи расчета устойчивости электрических системСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте При анализе статической устойчивости возникает ряд задач, которые решаются в проектных и эксплуатационных организациях. К таким задачам относятся: 1. Расчет параметров предельных режимов (предельной передаваемой мощности по линиям энергосистемы, критического напряжения узловых точек системы, питающих нагрузку, и т.д). 2. Определение значений коэффициентов запаса. Вместе с коэффициентами запаса по напряжению и мощности могут вычисляться коэффициенты запаса по настроечным параметрам АРВ: где 3. Выбор мероприятий по повышению статической устойчивости энергосистем или обеспечению заданной пропускной способности передачи. 4. Разработка требований, направленных на улучшение устойчивости систем. Выбирается настройка АРВ, обеспечивающая требуемую точность поддержания напряжения. Решение перечисленных задач проводится с учетом возможности возникновения самораскачивания системы. Задачи анализа динамической устойчивости связаны с переходом системы от одного установившегося режима к другому. Это следующие задачи: а) расчет параметров динамического перехода при эксплуатационном или аварийном отключениях нагруженных элементов электрической системы; б) определение параметров динамических переходов при коротких замыканиях в системе с учетом различных факторов: - возможного перехода одного несимметричного КЗ в другое (например, однофазного в двухфазное); - работы автоматического повторного включения элемента, отключившегося после КЗ, и т.д. Результатами расчета динамической устойчивости являются: - предельное время отключения расчетного вида КЗ в наиболее опасных точках системы; - паузы систем АПВ, установленных на различных элементах электрической системы; - параметры систем автоматического ввода резерва (АВР). Расчеты ведутся, как правило, с учетом нелинейностей и существенных динамических характеристик.
3. Статическая устойчивость простейшей системы Под простейшей системой понимается такая, в которой одиночная электростанция (эквивалентный генератор) связана с шинами (системой) неизменного напряжения трансформаторами и линиями, по которым передается мощность от станции в систему (см. рисунок 10.1). Принимается, что суммарная мощность электрических станций системы во много раз превышает мощность рассматриваемой станции. Это позволяет считать напряжение на шинах системы неизменным (U = const) при любых режимах ее работы.
Рисунок 10.1
На рисунке 10.2 дана схема замещения данной электропередачи, в которой отсутствуют активные сопротивления и емкости и элементы схемы представлены только их индуктивными сопротивлениями.
Рисунок 10.2
Сумма индуктивных сопротивлений генераторов, трансформаторов и линий дает результирующее индуктивное сопротивление системы:
Хс = Хг + Хт1 + 0,5Хл + Хт2.
Здесь, и в дальнейшем, под индуктивным сопротивлением генератора следует понимать его переходное сопротивление
На рисунке 10.3 показана векторная диаграмма нормального режима работы электропередачи, из которой ввиду равенства отрезков ОА = E sinδ и ВС = Iа Хс вытекает соотношение
где Iа – активный ток; δ – угол сдвига вектора ЭДС Умножая обе части равенства на U/Xc, получим:
или
где Р – активная мощность, выдаваемая генератором;
Зависимость (10.1) имеет синусоидальный характер и называется характеристикой мощности генератора.. С увеличением угла δ мощность Р сначала возрастает, но затем, достигнув максимального значения, начинает падать (см. рисунок 10.4).
Рисунок 10.3
При данном значении ЭДС генератора Е и напряжения приемника U существует определенный максимум передаваемой мощности
который называется идеальным пределом мощности рассматриваемой простейшей электрической системы. Равновесие между мощностью турбины и генератора достигается лишь при значениях мощности меньших Рm, причем данному значению мощности турбины Ро соответствуют две возможные точки равновесия на характеристике мощности генератора и, следовательно, два значения угла δа и δb (см. рисунок 10.4). Однако в действительности устойчивый установившийся режим работы электропередачи возможен только при угле δа. Режим в точке b на падающей части характеристики неустойчив и длительно существовать не может.
Рисунок 10.4
Рассмотрим режим работы в точке а. В этой точке мощности турбины и генератора уравновешивают друг друга. Если допустить, что угол δа получает небольшое приращение Δδ, то мощность генератора по синусоидальной зависимости от угла также изменится на величину ΔР, причем в точке а положительному приращению угла Δδ соответствует также положительное изменение мощности генератора ΔР. Мощность турбины не зависит от угла δ и при любых его изменениях остается постоянной и равной Ро. В результате изменения мощности генератора равновесие моментов турбины и генератора оказывается нарушенным и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора в силу положительного изменения мощности ΔР преобладает над вращающим моментом турбины. Под влиянием тормозящего момента ротор генератора начинает замедляться, что обусловливает перемещение связанного с ротором вектора ЭДС Совершенно другая получается картина в точке b. Здесь положительное приращение угла Δδ сопровождается не положительным, а отрицательным изменением мощности генератора ΔР. Изменение мощности генератора вызывает появление избыточного момента ускоряющего характера, под влиянием которого угол δ не уменьшается, а возрастает. С ростом угла мощность генератора продолжает падать, что приводит к дальнейшему увеличению угла и т.д. Процесс сопровождается непрерывным перемещением вектора ЭДС
Рисунок 10.5
Точка а и любая другая точка на возрастающей части синусоидальной характеристики мощности отвечают статически устойчивым режимам и, наоборот, все точки падающей части характеристики – статически неустойчивым. Формальным признаком статической устойчивости электрической системы может служить знак приращения мощности к приращению угла. Если ΔР/Δδ > 0, то система устойчива, если это отношение отрицательно, то неустойчива. Переходя к пределу, можно записать критерий устойчивости простейшей системы:
Увеличение мощности турбины приводит к возрастанию угла ротора и уменьшению запаса статической устойчивости. Запас устойчивости электропередачи, связывающей станцию с шинами энергосистемы, должен быть не менее 20% в нормальном режиме и 8% в кратковременном послеаварийном.
5. Уравнение движения ротора генератора Незначительное возмущение в цепи статора генератора вызывает движение ротора в сторону увеличения или уменьшения угла δ (это зависит от знака избыточного момента). Возмущение сообщает ротору некоторое ускорение α, которое в относительных единицах пропорционально избыточному моменту ΔМ и обратно пропорционально постоянной инерции Tj:
Здесь принимается, что при небольших изменениях скорости
где GD2 – маховый момент, т м2; n – скорость вращения, об/мин; Sном – номинальная мощность генератора, кВА. Возвращаясь к уравнению (11.2) и учитывая, что ускорение представляет собой вторую производную от угла по времени
получаем
Pmax – максимальное значение мощности аварийного режима. Уравнение (11.4) называется уравнением движения ротора генератора. Его решение в форме δ = f(t) дает картину изменения угла δ во времени и позволяет судить об устойчивости генератора.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1069; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

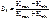
 и
и  - максимальное и минимальное значение настроечных параметров, соответствующих границе области статической устойчивости.
- максимальное и минимальное значение настроечных параметров, соответствующих границе области статической устойчивости.
 .
.
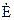 относительно вектора напряжения приемной системы
относительно вектора напряжения приемной системы 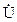 .
. ,
, (10.1)
(10.1) - переходная ЭДС генератора.
- переходная ЭДС генератора.
 , (10.2)
, (10.2)

 > 0.
> 0. . (11.1)
. (11.1) ; Tj – время, в течение которого скорость ротора изменяется от нуля до номинальной под действием номинального избыточного момента и при постоянном моменте сопротивления. Оно определяется:
; Tj – время, в течение которого скорость ротора изменяется от нуля до номинальной под действием номинального избыточного момента и при постоянном моменте сопротивления. Оно определяется: (с) (11.2)
(с) (11.2) ,
, (где Ро – мощность турбины;
(где Ро – мощность турбины;


