Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод последовательных интерваловСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Метод последовательных интервалов позволяет установить предельное время отключения КЗ, учесть действие регуляторов возбуждения, изменение реакции якоря во времени и т.д. Рассмотрим уравнение движения ротора генератора
Решение этого уравнения в форме δ = f(t) дает картину изменения угла во времени и позволяет установить, остается ли генератор в синхронизме. Однако это уравнение нелинейно и не может быть решено в общем виде (за исключением частного случая Рmax = 0). Задачу приходится решать методами численного интегрирования уравнений. Одним из них является рассматриваемый метод последовательных интервалов. Для этого весь процесс качания генератора разбивается на ряд небольших интервалов времени Δt и для каждого из этих интервалов последовательно вычисляется приближенное значение приращения Δδ. В момент КЗ отдаваемая генераторами мощность падает и возникает некоторый избыток мощности ΔР(0). Для достаточно малого интервала времени Δt можно допустить, что избыток мощности в течение этого интервала остается неизменным. Тогда по формулам равномерно ускоренного движения можно определить приращение скорости генератора Δv(1) и угла Δδ(1) в течение первого интервала: Относительная скорость машины в момент КЗ равна нулю, и поэтому относительная скорость v(1) в конце первого интервала равна приращению скорости в течение этого интервала, т.е. v(1) = Δ v(1). Ускорение α(0) определяется
следовательно,
здесь угол и время выражены в радианах. В практических расчетах удобнее пользоваться выражением угла в градусах
и времени в секундах
Используя (14.2) и (14.3) и принимая во внимание, что
где угол выражен в градусах, а время и постоянная инерции – в секундах. Обозначая далее
Зная приращение угла в первом интервале, можно найти абсолютное значение угла в конце этого интервала времени или, что то же самое, в начале следующего интервала: Для нового значения угла δ(1) можно определить избыток мощности ΔР(1) во втором интервале времени по формуле
Избыток мощности ΔР(1) создает во втором интервале пропорциональное ему ускорение α(1). При вычислении приращения угла Δδ(2) в течение второго интервала (а также и всех последующих) помимо действующего в этом интервале ускорения α(1) необходимо учесть также уже имеющуюся в начале интервала относительную скорость ротора:
Значение скорости v1, получаемой из формулы v(1)= α(0)Δt, является неточным, так как в действительности избыток мощности ΔР(0) и ускорение α(0) не являются постоянными в течение первого интервала времени, а несколько изменяются. Более точные результаты можно получить, если предположить, что ускорение в первом интервале было равно среднему значению
Тогда относительная скорость
Подставляя это значение в (14.6), находим:
или
и так далее. Теперь можно найти угол
и так далее. Если в начале некоторого к -го интервала происходит отключение поврежденной цепи, то избыток мощности внезапно изменяется от некоторой величины
Рисунок 14.1
При вычислении приращения угла в первом интервале после момента отключения значение избытка мощности определяется как среднее из
В дальнейших интервалах можно снова пользоваться (14.7). Значение интервала времени Δt при ручном счете принимается обычно равным 0,05 с. Расчет методом последовательных интервалов ведется до тех пор, пока угол δ не начнет уменьшаться или пока не будет ясным, что угол беспредельно возрастает, т.е. генератор выпадает из синхронизма. Метод последовательных интервалов можно применять совместно с правилом площадей. Для этого, пользуясь правилом площадей, определяют предельный угол δотк, при котором должно произойти отключение КЗ, и с помощью метода последовательных интервалов определяют время, в течение которого ротор достигает угла δотк. Этот промежуток времени и дает предельное время отключения (см. рисунок 14.2).
Рисунок 14.2
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 472; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.242 (0.007 с.) |

 .
.
 ;
;  .
. ,
, , (14.1)
, (14.1) (14.2)
(14.2) . (14.3)
. (14.3) , получаем:
, получаем: (14.4)
(14.4) , окончательно получаем:
, окончательно получаем: . (14.5)
. (14.5)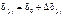 .
. .
. . (14.6)
. (14.6) .
. .
.
 (14.7)
(14.7) , определить избыток мощности ΔР(2) и приращение угла Δδ(3):
, определить избыток мощности ΔР(2) и приращение угла Δδ(3):
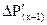 до величины
до величины  (см. рисунок 14.1).
(см. рисунок 14.1).
 и
и  , т.е.
, т.е. . (14.8)
. (14.8)