
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы оценки качества продукцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотренные в п. 3.4 показатели качества продукции и в 3.6 методы их определения не решают в целом проблему определения количественно столь емкой и сложной категории как качество продукции. Для этого существуют и применяются методы оценки качества продукции. Под методом оценки качества продукции (МОКП) понимается совокупность логических и математических операций по использованию отдельных ПКП или их определенного сочетания для определения качества изделия в целом на основе их сравнения с аналогичными вариантами изделий для принятия решения о выборе предпочтительного (лучшего) по качеству для потребителя варианта. ГОСТ 15467–79 предусматривает следующие МОКП: дифференциальный, комплексный, смешанный и статистический методы. Дифференциальный МОКП — метод оценки качества продукции, основанный на использовании единичных показателей ее качества. Этот метод заключается в систематизации и сравнительном анализе значений совокупности единичных показателей, характерных для каждого из сравниваемых вариантов, и принятии на этой основе решения о предпочтительности одного из вариантов, обладающего лучшим набором единичных показателей. В изложенной сущности этого метода существует противоречие, затрудняющее широкое использование этого метода по прямому назначению, заключающемуся в выборе лучшего варианта изделия из всей совокупности однотипных изделий, различающихся значениями различных единичных показателей. Дело в том, что единичные показатели от варианта к варианту изменяются не однонаправленно, например, только улучшаются. Обычно каждый вариант изделия отличается от остальных лучшими значениями одного или нескольких показателей и худшими в сравнении с другими вариантами значениями остальных единичных показателей. И это характерно не только для сложных, но и для сравнительно простых, малопараметрических изделий, например, таких элементов электронной техники, как резисторы, конденсаторы и др.; электробытовых изделий, обуви, одежды, которые характеризуются небольшим набором показателей, особенно показателей назначения. Для сложных же изделий, характеризующимися и различающимися десятками и сотнями единичных показателей принятие решение о выборе предпочтительного варианта становится неразрешимой задачей. Этот недостаток можно ослабить путем использования коэффициентов весомости отдельных единичных показателей, но это значительно повышает трудоемкость реализации метода, поскольку требует применения экспертных оценок для установления коэффициентов весомости показателей качества, что в свою очередь усиливает субъективность метода. Но и при органически присущих дифференциальному МОКП недостатках он имеет самостоятельно применение по основному назначению в следующих основных случаях: · при анализе тенденций изменения отдельных единичных показателей и выработке рекомендаций по их достижению путем включения в опережающие стандарты; · при оценке качества сравнительно простых изделий, у которых один из показателей имеет высокую дискретность изменения значений в их широком диапазоне, а другие показатели имеют небольшую дискретность, например, резисторы, электродвигатели, бытовые электроприборы и т. п.; · при отсутствии вариативности в выборе изделий, поскольку значения большинства единичных показателей вытекают из расчета (например, значение емкости и допустимого напряжения конденсатора, мощность и число оборотов электродвигателя); антропометрических параметров (например, обувь, одежда и т. п., для которых вариативность в размерных показателях отсутствует, но сохраняется в эстетических) и др.; · при необходимости сопрягаемости показателей изделия с условиями его эксплуатации (напряжение питания прибора с напряжением сети, температурный режим эксплуатации изделия с климатическими условиями и т. п.) или сочетания цветового оформления изделия с интерьером и т. п. С учетом указанных особенностей дифференциального МО он имеет ограниченное применение на практике, а предпочтение отдается методам, позволяющим комплексно подойти к оценке качества продукции. Комплексный МОКП — метод оценки качества продукции, основанный на использовании комплексных показателей ее качества, т. е. показателей, характеризующих несколько свойств продукции. Основным подходом в реализации этого метода является построение комплексного показателя в виде определенной функции нескольких единичных показателей качества оцениваемого и сравниваемых с ним образцов продукции. Такой подход связан с принципиальными трудностями, заключающимися в следующем: · выбор комплексного показателя качества, т. е. показателя некоторого сложного свойства и его размерности; · в содержательном описании сложного свойства продукции, достаточно объективно и полно отражающем совокупность элементарных свойств, характеризуемых единичными показателями, и образующую качество этой продукции; · в установлении функциональной зависимости комплексного показателя качества от единичных показателей, которая во многих случаях неизвестна; · во взаимной компенсации одних показателей за счет других, т. е. при разном наборе значений единичных показателей, комплексный показатель может оказаться одинаковым или близким по величине у сравниваемых вариантов однотипной продукции; · установленная функция может носить немонотонный характер, что приведет к неоднозначности в оценке качества продукции. Преодоление отмеченных трудностей обеспечивается использованием достижений современной науки в области оцениваемой техники и привлечением опытных специалистов в качестве экспертов для установления неочевидных с точки зрения физико-химических процессов зависимостей между комплексным и единичными показателями.. Другой распространенный подход к построению комплексного ПКП состоит в следующем. Обоснование функциональной зависимости комплексного ПКП от единичных в тех случаях, когда она неизвестна, облегчается тем обстоятельством, что сравнение однотипных видов продукции обычно осуществляется при небольших различиях значений показателей качества сравниваемых вариантов (образцов) продукции. Благодаря этому можно ограничиться при разложении комплексного показателя в ряд Тейлора членами, содержащими первые степени аргумента, в качестве которого фигурируют единичные показатели качества сравниваемых вариантов, с последующей математической обработкой [47]. Комплексный МОКП, как правило, сопряжен с необходимостью определения коэффициентов весомости единичных показателей, правильность установления которых имеет важное значение для результатов комплексной оценки качества, существенно влияя на ее корректность. Для определения коэффициентов весомости ПКП при комплексной оценке ее качества применяются аналитические и экспертные методы соответственно по ГОСТ 24294–80 и ГОСТ 23554.0–79, ГОСТ 23554.1–79. В ГОСТ 24294–80 приведен метод регрессионных зависимостей и метод эквивалентных соотношений. В основу этого стандарта положен принцип установления соответствия между комплексным ПКП, имеющим реальное смысловое содержание и наиболее полно отражающим степень удовлетворения данной продукцией потребностей, и единичными ПКП. Необходимые для этого исходные данные имеются в каталогах, научной литературе, НТД. В тех случаях, когда таких данных нет, их получают экспериментальным путем. В ГОСТ 23554.0–79 и ГОСТ 23554.1–79 в комплексе вопросов порядка и организации экспертной оценки качества продукции приведены указания по установлению коэффициентов весомости экспертами. В практике оценки качества продукции часто встречаются случаи, когда одновременно необходимо знать комплексный ПКП, анализировать единичные показатели, выявлять возможности их улучшения. В этих случаях применяется смешанный метод оценки, под которым согласно ГОСТ 15467–79 понимается метод оценки качества продукции, основанный на одновременном использовании единичных и комплексных показателей ее качества. Этот метод объединяет дифференциальный и комплексный методы, сущность и методические особенности которых рассмотрены выше. В составе МОКП выделяется статистический метод, под которым согласно ГОСТ 15467–79 понимается метод оценки качества продукции, при котором значения показателей качества продукции определяют с использованием привил математической статистики. Необходимость применения методов математической статистики при оценке ПКП обусловлена тем, что в большинстве случаев значения ПКП являются случайными величинами вследствие воздействия многочисленных случайных факторов в процессе производства и эксплуатации продукции. В связи с этим в практике оценки качества продукции возникает ряд характерных статистических задач: · установить характер и причину различия показателей качества сравниваемых вариантов продукции; · определить коэффициент корреляции (вероятностной связи) между ПКП; · определить параметры зависимости исследуемого ПКП от численных характеристик влияющих на него факторов; · определить влияние различных факторов на изменение ПКП; · определить точность и устойчивость технологического процесса и их влияние на закон распределения формируемого этим процессом ПКП. Для решения этих и других подобных задач оценки качества продукции применяются методы теории вероятностей и математической статистики, среди которых наиболее характерными являются: точечное и интервальное оценивание параметров распределения показателей качества; проверка гипотез; дисперсионный анализ; корреляционный анализ; регрессионный анализ; анализ временных рядов, последовательностей процессов и др. Точечное и интервальное оценивание параметров закона распределения случайных величин ПКП хорошо иллюстрируется оценкой таких показателей, как наработка до отказа неремонтируемых технических устройств, срок сохранения быстро портящейся пищевой и фармацевтической продукции, прочностные характеристики материалов при различных способах приложения нагрузки, прочность на пробой изоляционных материалов и т. п. Статистическая оценка (точечная и интервальная) указанных ПКП в значительной степени зависит от выбора вида его закона распределения, который определяется характером физико-химических процессов в структуре материалов. Выявление и обоснование закона распределения ПКП вызывает необходимость проведения статистических исследований. В составе многочисленных методов точечного оценивания параметров закона распределения ПКП наибольшее применение получили метод максимума правдоподобия, метод моментов, байесовское оценивание и др. Методы интервального оценивания позволяют установить интервал, в котором с заданной доверительной вероятностью находятся значения исследуемых параметров распределения ПКП, что играет важную роль для обоснования предъявляемых к ПКП требований и норм. Для оценки доверительных интервалов параметров нормального, логарифмически нормального, экспоненциального, биномиального распределений, законов Пуассона и Вейбулла, как наиболее характерных для распределения ПКП, используются государственные стандарты серии 11 (ГОСТ 11.010–81 и др.). В этих стандартах содержатся простые правила и таблицы для оценки доверительных интервалов параметров указанных распределений с заданной вероятностью. Проверка гипотез заключается в том, что справедливость выдвинутой гипотезы проверяется по результатам наблюдений случайной величины ПКП с заданной доверительной вероятностью. Характерным примером является оценка доли дефектности совокупности единиц продукции по результатам выборочного контроля ее качества, выборочного контроля параметров технологического процесса при построении контрольных диаграмм его качества и др. Дисперсионный анализ основан на сравнении дисперсий двух выборок, которое позволяет с заданной доверительной вероятностью относить их принадлежность к одной и той же совокупности или считать такую принадлежность маловероятной. Этот метод применяется в тех случаях, когда требуется оценить влияние определенного фактора на изменение рассматриваемого ПКП. Методы корреляционного и регрессионного анализа при некоторых различиях основаны на единых предпосылках. Корреляционный анализ представляет собой совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами. При этом две случайные величины считаются корреляционно связанными, если математическое ожидание одной из них меняется в зависимости от изменения другой. Корреляционный анализ экспериментальных данных включает в себя следующие приемы: · составление корреляционной таблицы; · вычисление коэффициентов корреляции; · проверка статистической гипотезы значимости связи. Зависимость между тремя и большим числом случайных признаков или факторов изучается методами многомерного корреляционного анализа (вычисление частных и множественных коэффициентов корреляции и корреляционных отношений). Корреляционный анализ часто применяется для оценки зависимости качества конечной продукции от определенных свойств сырья или исходных материалов. Этот вид анализа требует от исполнителя тщательности, так как при изменении условий эксперимента вместе с изменением исследуемого показателя качества сырья или материала могут изменяться и другие показатели их качества. Если эти изменения не будут учтены, возникнут значительные ошибки в окончательном результате. Связь между случайной и неслучайной величинами называется регрессионной, а метод анализа таких связей — регрессионным анализом. Регрессионный анализ тесно связан с корреляционным, но в то же время он предъявляет менее жесткие требования к исходной информации (так, например, проведение регрессионного анализа, в отличие от корреляционного, возможно даже в случае отличия распределения случайной величины от нормального). Регрессионный анализ заключается в исследовании распределения коэффициентов регрессии, определяющих случайную величину как функцию от нескольких других. Определение неизвестных коэффициентов регрессии и дисперсии осуществляется методом наименьших квадратов. Этот метод в предположении нормальной распределенности результатов наблюдений приводит к оценкам, совпадающим с оценками наибольшего правдоподобия. Значимость оценок и их доверительные интервалы определяются с применением аппарата и критериев проверки статистических гипотез. Регрессионный анализ применяется для исследования поведения коэффициентов весомости при комплексной оценке качества продукции. Требование нормальности распределения ошибок, предъявляемое к исходной информации процедурой метода наименьших квадратов, во многих случаях оказывается невыполненным, что приводит к снижению достоверности оценок. Поэтому развивается новое направление — робастная статистика, задача которой состоит в том, чтобы получать эффективные оценки в случаях невыполнения некоторых предпосылок применения корреляционного и регрессионного анализа (например, нормальности распределения). Использование робастных методов получения статистических оценок позволяет существенно повысить надежность оценок в сравнении с методом наименьших квадратов. При оценке и анализе показателей и процессов, подверженных влиянию большого количества случайных факторов, с учетом требования адекватности является снижение размерности их описания. Эта задача успешно решается с использованием факторного анализа, основным содержанием которого является расчет и анализ корреляционной матрицы признаков, позволяющей осуществить переход к другой координатной системе, обладающей рядом необходимых для статистического анализа новых свойств, и позволяющей снизить размерность описания показателей и процессов. В качестве инструмента факторного анализа при построении и анализе корреляционной матрицы используются методы «главных компонент» и «главных факторов» [40]. Временным рядом в математической статистике называется упорядоченная последовательность результатов наблюдений некоторой величины, определенным образом меняющейся во времени. Временным рядом является, например, упорядоченная последовательность значений ПКП, полученных в последовательные моменты времени. Методы анализа временных рядов могут эффективно применяться при исследовании динамики качества продукции. Предусмотренные ГОСТ 15467–79 и рассмотренные выше методы оценки качества продукции имеют определенную результативность и области применения, но не устраняют полностью неопределенность при оценке качества, возникающую вследствие разнонаправленных, неупорядоченных значений ПКП у сравниваемых вариантов продукции (у одних изделий лучше один набор параметров, чем у остальных, у других — свой набор и т. д.). Это затрудняет обоснованный выбор изделия, обладающего более высоким в сравнении с другими однотипными изделиями качеством. Преодоление этой трудности позволяет осуществить обобщенный метод оценки качества продукции, состоящий в формировании обобщенного ПКП, объединяющего в единый по определенному алгоритму или правилу все единичные и комплексные ПКП. При этом могут быть использованы различные алгоритмы формирования обобщенного ПКП: аддитивный, мультипликативный, метод оптимальной классификации или таксономии и др. При обозначениях: qi и аддитивному (средневзвешенному):
гармонически средневзвешенному
при общем условии мультипликативному В выражении (3.5) при коэффициенте весомости ставится знак «+», если при увеличении i -го показателя качество продукции улучшается, и знак «–», если ухудшается, т. е. обобщенный показатель представляется в виде дроби, в числителе которой стоят показатели, при увеличении которых качество повышается, в знаменателе, при уменьшении которых качество повышается. Основным и общим недостатком всех приведенных алгоритмов является преобладающее влияние на величину обобщенного показателя одного или нескольких единичных показателей при их экстремальных (значительно больших или значительно меньших, чем у остальных) значений, т. е. формирование обобщенного показателя в основном за счет одного или нескольких единичных (например, достаточно устремить к нулю значение одного из показателей, стоящих в знаменателе дроби, т. е. при знаке «–» при коэффициенте весомости в выражении (3.5), как резко устремляется в ¥ значение обобщенного показателя. Этот недостаток можно преодолеть, если ограничить значения каждого единичного показателя некоторыми, вытекающими из интересов потребителя пределами. Дополнительным недостатком первых двух алгоритмов является необходимость нормирования единичных показателей качества (представления их в виде отношения значений единичных показателей оцениваемого и базового образцов) для перевода их в безразмерные, иначе будет нарушено известное в математике «условие подобия». Все рассмотренные недостатки приведенных алгоритмов формирования обобщенного ПКП можно преодолеть применением метода оптимальной классификации как разновидности методов таксономии [40,43], суть которого состоит в следующем. Каждый из обобщенных показателей строится в n -мерном (по количеству n единичных показателей) пространстве. Координатами каждого из векторов обобщенных показателей являются значения соответствующих единичных показателей на i -той оси n -мерного векторного пространства. Решение о выборе лучшего по качеству варианта продукции принимается путем оценки расстояния от вершины вектора или точки в n -мерном пространстве до вершины вектора (точки), соответствующей значению обобщенного показателя качества варианта-эталона, который может быть сформирован путем придания ему лучших значений единичных показателей, присущих сравниваемым вариантам продукции или создан искусственно путем придания ему желательных потребителю значений каждого из единичных показателей. Возможны и другие методы и алгоритмы построения обобщенного показателя качества, позволяющие обеспечить повышение объективности и определенности в оценке качества продукции и обоснованность выбора потребителем лучшего по качеству из сравниваемых вариантов оптимальной классификации [40].
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.025 с.) |

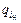 — соответственно абсолютные и нормированные значения i -го единичного показателя; n — количество учитываемых единичных показателей; bi — коэффициент весомости i -го единичного показателя формирование обобщенного ПКП может строиться по алгоритмам:
— соответственно абсолютные и нормированные значения i -го единичного показателя; n — количество учитываемых единичных показателей; bi — коэффициент весомости i -го единичного показателя формирование обобщенного ПКП может строиться по алгоритмам: (3.2)
(3.2) (3.3)
(3.3) (3.4)
(3.4) . (3.5)
. (3.5)


